一文带你直观理解线性变换

笔者是一名软件工程专硕的研一小菜鸡，若是文章中出现纰漏，请不吝赐教。
本篇笔记仅供交流学习，如需转载请注明出处。

一、线性变换的定义

百度百科关于线性变换的定义如下：

线性映射（ linear mapping）是从一个向量空间V到另一个向量空间W的映射且保持加法运算和数量乘法运算，而线性变换（linear transformation）是线性空间V到其自身的线性映射。

这里的意思是线性映射是由向量空间\( V \rightarrow W \) 的映射，而线性变换是线性映射的一个特例，是由线性空间\( V \)到其自身的映射。

维基百科关于线性映射的定义如下：

In mathematics, and more specifically in linear algebra, a linear map (also called a linear mapping, linear transformation, vector space homomorphism, or in some contexts linear function) is a mapping)\( \displaystyle V\to W \)between two vector spaces that preserves the operations of vector addition and scalar multiplication.

大体翻译一下：在数学中，更具体地说是在线性代数中，线性映射（也被称为线性变换、向量空间同态，或者在某些情况下也被叫做线性函数）是一种\( \displaystyle V\to W \)的映射，这种映射保留了向量加法和标量乘法运算。

从维基百科的定义来看，可以不用区分线性映射和线性变换。

二、如何判断是否为线性变换

你可以将线性变换理解为一个特殊的函数，这个可以使得\( \displaystyle V\to W \)，并且满足以下条件：

$$ \begin{array}{l} \mathbf{T}(\mathbf{x}+\mathbf{y})=\mathbf{T}(\mathbf{x})+\mathbf{T}(\mathbf{y}) \\ \mathbf{T}(a \mathbf{x})=a \mathbf{T}(\mathbf{x}) \end{array}\tag{1} $$

其中\( x,y \in V \)，\( a \in R \)

识别给定函数\( f(x) \)是否为线性变换非常简单，只需要查看\( f(x) \)中的每一项是否都是\( x \)与一个数的乘积，如果是，\( f \)则是线性变换。

举个例子：

$$ \mathbf{f}(x, y, z)=(3 x-y, 3 z, 0, z-2 x)\tag{2} $$

便是一个线性变换，而

$$ \mathbf{g}(x, y, z)=(3 x-y, 3 z+2,0, z-2 x) \\ \mathbf{h}(x, y, z)=(3 x-y, 3 x z, 0, z-2 x) \tag{3} $$

这两个都不是线性变换。因为在函数\( g \)中，第二个分量为\( 3z+2 \)，\( 2 \)是一个常数，并不包含输入向量\( (x,y,z) \)中的任何分量，也可以换种解释方法，按照\( (1) \)中的第二个公式，应有\( \mathbf{T}(\mathbf{0})=\mathbf{0} \)，而\( g(0,0,0)=(0,2,0,0) \)与上式矛盾。在函数\( h \)中，很明显含有一个非线性分量\( 3xz \)，因此也不是一个线性变换。

三、线性变换的直观解释

本篇文章最重要的部分终于来了，废话不多说，直接进入正题。

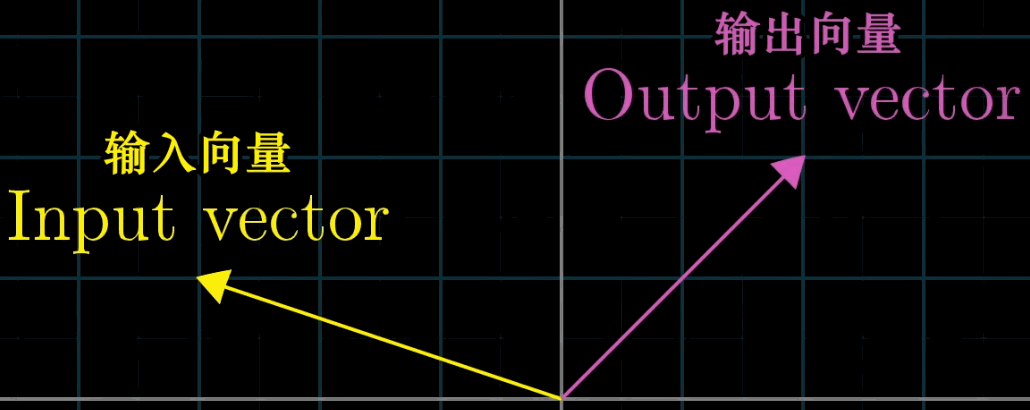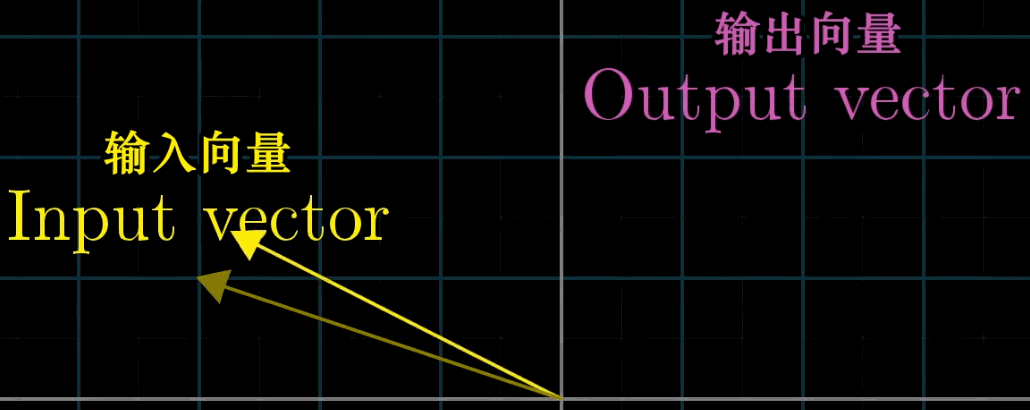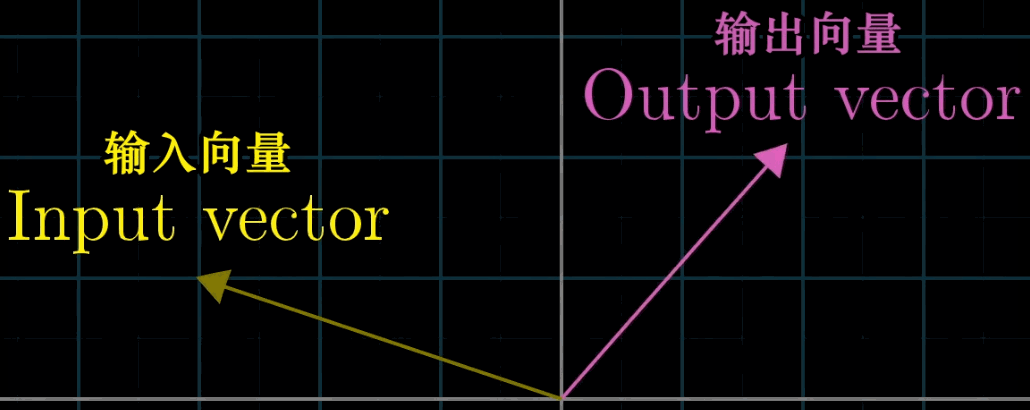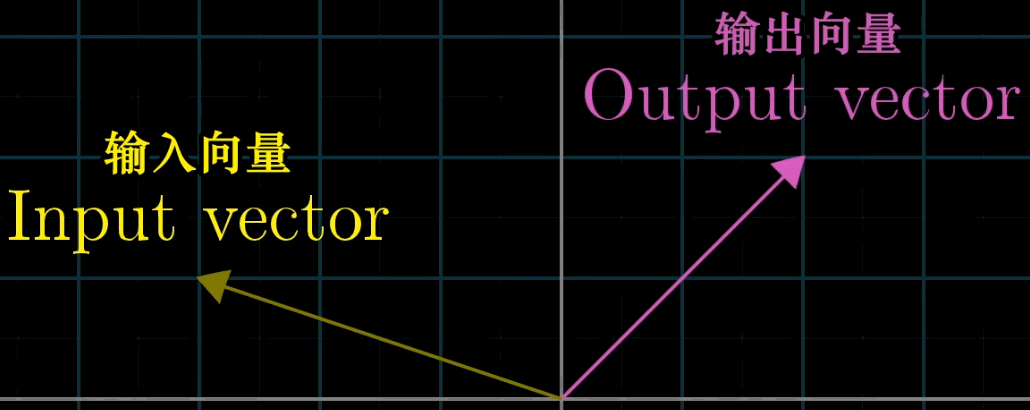
变换本质上是函数，其接受一个输入，然后输出对应的结果。之所以叫变换，是因为从几何的角度我们可以用运动的方式来理解变换，如旋转、伸缩、投影或几者叠加等操作。下面通过一个动图来演示一下。

那如何理解线性呢？其在几何直观上必须满足以下条件：

1. 变换前是直线，变换后依然是直线
2. 原点保持固定不动

也就是说，你应该把线性变换看作是“保持坐标网格平行并等距分布”的变换。

1、一点不太直观的东西

以前上线性代数课的时候老师肯定告诉过你，可以将下面这个式子

$$ \mathbf{f}(x, y)=(3 x-y, 2 x) \tag{4} $$

改写为：

$$ f\left(\left[\begin{array}{l} x \\ y \end{array}\right]\right)=\left[\begin{array}{cc} 3 & -1\\ 2 & 0 \end{array}\right]\left[\begin{array}{l} x \\ y \end{array}\right]\tag{5} $$

于是，这个线性变换就可以用一个矩阵来实现了。

2、该矩阵的本质

从上面的式子可以看出来，这个矩阵可以表示一个特定的线性变换，当这个矩阵与一个向量相乘则表示将这个特定的线性变换作用于该向量。那你有没有好奇过这个矩阵在几何空间中表示的是什么呢？下面以二维空间为例来说明。

如上图所示，\( \vec{A} \)可以看作是一个向量，可以表示为

$$ \vec{A}=\left[\begin{array}{l}3 \\2\end{array}\right] $$

也可以表示为\( \vec{A}=3 \vec{i}+2 \vec{j} \)，其中\( \vec{i} \)，\( \vec{j} \)是该向量空间的基向量。在本示例中

$$ \vec{i}=\left[\begin{array}{l}1 \\0\end{array}\right] $$

，

$$ \vec{j}=\left[\begin{array}{l}0 \\1\end{array}\right] $$

\( \vec{A} \)可以写成：

$$ \vec{A}=3\left[\begin{array}{l} 1 \\ 0 \end{array}\right]+2\left[\begin{array}{l} 0 \\ 1 \end{array}\right]=\left[\begin{array}{ll} 1 & 0 \\ 0 & 1 \end{array}\right]\left[\begin{array}{l} 3 \\ 2 \end{array}\right]\tag{6} $$

那如果我们将上面的向量空间进行旋转并拉伸得到如下所示的向量空间（其中坐标轴\( x,y \)仍然是原坐标轴，背景格也可以当作原坐标轴）：

原向量空间的基向量\( \vec{i} \)，\( \vec{j} \)经线性变换后为该向量空间中的\( \overrightarrow{i^{\prime}} \)，\( \overrightarrow{j^{\prime}} \)，可以看出这里的

$$ \overrightarrow{A^{\prime}}=3\overrightarrow{i^{\prime}}+2 \overrightarrow{j^{\prime}} $$

对应到原向量空间的坐标，

$$ \overrightarrow{i^{\prime}}=\left[\begin{array}{l}1 \\-2\end{array}\right] $$

$$ \overrightarrow{j^{\prime}}=\left[\begin{array}{l}3 \\0\end{array}\right] $$

\( \overrightarrow{A^{\prime}} \)可以表示为：

$$ \overrightarrow{A^{\prime}}=3\left[\begin{array}{l} 1 \\ -2 \end{array}\right]+2\left[\begin{array}{l} 3 \\ 0 \end{array}\right]=\left[\begin{array}{ll} 1 & 3 \\ -2 & 0 \end{array}\right]\left[\begin{array}{l} 3 \\ 2 \end{array}\right]\tag{7} $$

对比公式\( (7) \)和公式\( (6) \)可以看出唯一变化的就是左乘的矩阵，而这两个矩阵都是各自向量空间中的基向量的坐标拼起来的，即：

$$ \begin{aligned} \left[\begin{array}{ll} 1 & 0 \\ 0 & 1 \end{array}\right] &=\left[\begin{array}{ll} \vec{i} & \vec{j} \end{array}\right] \\ \left[\begin{array}{ll} 1 & 3 \\ -2 & 0 \end{array}\right] &=\left[\begin{array}{ll} \overrightarrow{i^{\prime}} & \overrightarrow{j^{\prime}} \end{array}\right] \end{aligned} \tag{8} $$

我们再将公式\( (7) \)改变一下，可以写成：

$$ \overrightarrow{A^{\prime}}=\left[\begin{array}{ll} 1 & 3 \\ -2 & 0 \end{array}\right]\left[\begin{array}{l} 3 \\ 2 \end{array}\right]=\left[\begin{array}{ll} 1 & 3 \\ -2 & 0 \end{array}\right]\vec{A}\tag{9} $$

前面已经说过了

$$ \vec{A}=\left[\begin{array}{l}3 \\2\end{array}\right] $$

矩阵

$$ \left[\begin{array}{ll} 1 & 3 \\ -2 & 0 \end{array}\right]=\left[\begin{array}{ll} \overrightarrow{i^{\prime}} & \overrightarrow{j^{\prime}} \end{array}\right] $$

。

到这里不难看出，实际上线性变换是改变了基向量（当然这么说不严谨），可以这么理解。矩阵的列其实就是变换后的基向量\( \overrightarrow{i^{\prime}} \)， \( \overrightarrow{j^{\prime}} \)，这就是该矩阵的真正含义。你可以将这里的矩阵理解为一个记号，它描述了一个线性变换，矩阵的第一列可以看作是变换后的第一个基向量的落脚点，矩阵的第二列看作是变换后的第二个基向量的落脚点。

3. 推广

到这里这篇文章已经接近尾声，那我们再将这里的结论推广一下：

你可以理解为一个二维空间中的线性变换可以由四个数字确定，即一个\( 2*2 \)矩阵确定，如

$$ \left[\begin{array}{ll} a & b \\ c & d \end{array}\right] $$

\( (a, c) \)就看作是变换后第一个基向量的落脚点，\( (b, d) \)看作是变换后第二个基向量的落脚点。当你想知道任意一个向量

$$ \vec{B}=\left[\begin{array}{l}x \\ y\end{array}\right] $$

经过此线性变换后得到的结果\( \overrightarrow{B^{\prime}} \)，即

$$ \overrightarrow{B^{\prime}}=\left[\begin{array}{ll} a & b \\ c & d \end{array}\right]\left[\begin{array}{l} x \\ y \end{array}\right]\tag{10} $$

本文到此结束，感谢阅读～