公众号:DS数说
作者:xihuishaw
1个月未更新了,年底事情比较多(社畜都懂得~)。上月底报名了百度飞桨的一个常规赛-- MarTech Challenge 点击反欺诈预测 ,搞了一周(社畜只能下班熬夜搞!),运气比较好,水到了Top1。
这个比赛是常规的结构化比赛,主要就是根据业务理解进行特征工程 + LGB/XGB集成模型调参、融模。但如果想对这些Boosting算法用起来得心应手的话,还是先要把决策树弄明白。这个非常重要的机器学习模型有很多资料和书籍进行讲解,我这纯属班门弄斧。
之前也从未总结过,趁着这个机会总结一下所看的一些资料,重点是讲清楚决策树中特征选择与切分点。
那就直接进入主题~
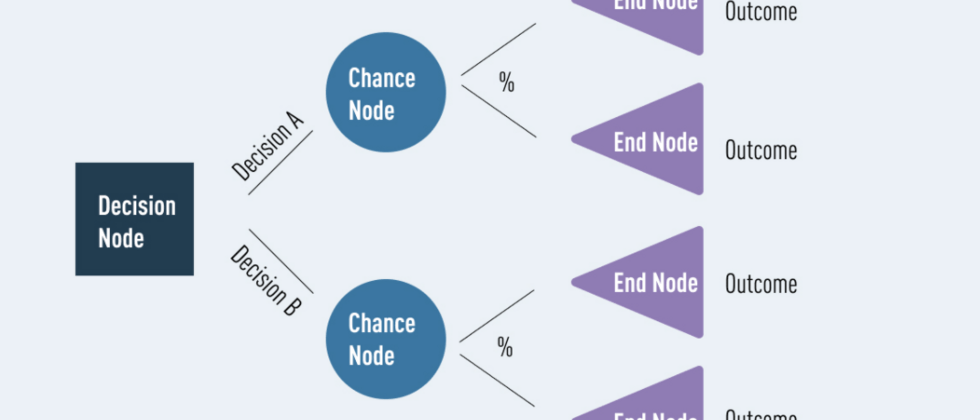
决策树的思想是,用节点代表样本集合,通过某些判定条件来对节点内的样本进行分配,将它们划分到该节点下的子节点,并且要求各个子节点中类别的纯度之和应高于该节点中的类别纯度,从而起到分类效果。
决策树学习的本质是,从训练数据集中归纳出一组分类规则。
构造决策树
递归地选择最优特征(能将数据集往“纯度”更高的方向划分),依次直到不能划分为止(所有子集被基本正确分类或者没有合适特征为止)。
这个过程是局部最优的,因为<u>每个节点的划分都是选择当前条件下最好的分类</u>,没有考虑后面的节点划分情况,从全局看未必是最优,仅是次优解,并且这种启发式的贪心算法,容易产生过拟合,模型泛化能力差。
但,我们可以从下往上对决策树进行剪枝(pruning),剪去过于细分的叶节点,回退到父节点并更改为叶节点,提升模型的泛化能力,这也是考虑全局最优的方式。
关键问题:如何选择合适的特征以及该特征对应的切分位置
切分点查找、评估方式
特征选择的准则:该特征具有很强的分类能力。
1、信息增益(Information Gain)
也叫熵减, Entropy Decrease,熵是描述信息不确定状态的一种度量,值越大则越不稳定(事件发生的概率越低,所包含的信息量越大)。
信息增益 = 父节点信息熵 - 按某特征分割后子节点条件熵
其中条件熵指的是,节点分裂之后带来了多少不确定性的降低或纯度的提高:
在每一个小类里面,都计算一个小熵,然后每一个小熵乘以各个类别的概率,然后求和。
所以,信息增益代表随机变量X的取值,降低了Y的不确定性的平均减少量。
举例:
递归选择信息增益最大的特征作为切分特征。
但是,如果遇到那种uuid、编号等特征,模型很容易将一个id处理成一类,此时条件熵往往等于0,信息增益肯定最大,这里就会陷入特征选择的误区。这并不是我们想要的分类,容易过拟合。
所以说,信息增益更偏好于选择取值较多的特征。
2、信息增益比(Gain Ratio)
信息增益比可以很好的校正信息增益的问题。分子还是信息增益,分母为一个惩罚项,即特征不同取值下的熵之和。
当分裂数很多的时候(比如一个id对应着一个类),惩罚项会变大,分裂算法可有效避免选择这类特征做分裂。
小结
「信息增益」不能完全反应一个「分裂」的有效性, 通过改造使用「信息增益比」公式,可以有效避免决策树分裂策略使用类似「uuid」、「编号」类的取值量特别大的特征,陷入「最大化信息增益」的误区中。
特征分裂应该使用「二叉树」还是「多叉树」也可以从这个例子中得到启发,二叉树的特性使它自带抑制「过拟合」的功能,毕竟二叉树不能一下子直接分完,多叉树是可能一次性直接将样本分完。
决策树生成算法
ID3 :信息增益
- 没有剪枝策略,容易过拟合;
- 信息增益准则
对可取值数目较多的特征有所偏好,类似“编号”的特征其信息增益接近于 1; - 只能用于处理离散分布的特征;
- 没有考虑缺失值;
C4.5:信息增益比
连续特征离散化:假设 n 个样本的连续特征 A 有 m 个取值,C4.5 将其排序并取相邻两样本值的平均数共 m-1 个划分点,分别计算以该划分点作为二元分类点时的信息增益,并选择信息增益最大的点作为该连续特征的二元离散分类点;- C4.5 只能用于分类;
- C4.5 使用的熵模型拥有大量耗时的对数运算,连续值还有排序运算;
- C4.5 在构造树的过程中,对数值属性值需要按照其大小进行排序,从中选择一个分割点,所以只适合于能够驻留于内存的数据集,当训练集大得无法在内存容纳时,程序无法运行;
- CART
CART 算法的二分法可以简化决策树的规模,提高生成决策树的效率。
CART
CART,classification and regression tree,分类回归树,既可以用于分类也可以用于回归。
CART采用的二叉树递归,每个非叶子节点都有2个分支。
- 当CART是
分类树的时候,采用GINI值作为分裂节点的依据; - 当CART作为
回归树的时候,使用样本的最小方差作为分裂节点的依据。
1、回归树
最小二乘法 回归树生成算法:
选择某特征,将所有取值分为2类(分类有很多种,为1:n),计算2类对应的y的均值c,并计算2类取值的均方误差(yi-c)^2,遍历所有的分类情况,选择误差最小的切分情况。
示例:
2、分类树
分类树是用基尼指数选择最优特征,同时决定该特征的最优二值切分点。<u>基尼系数越小,不纯度越低,特征越好。</u>
示例:
3、剪枝
CART采用后剪枝法,即先生成决策树,然后产生所有剪枝后的CART树,然后使用交叉验证检验剪枝的效果,选择泛化能力最好的剪枝策略。
我们希望减少树的大小来防止过拟合(降低树的复杂度),但又担心去掉节点后预测误差会增大,所以定义一个损失函数来达到这两个变量之间的平衡。
损失函数定义如下:
C(T)为预测误差,|T|为子树T的叶子节点数(代表树的复杂度)
总结
划分标准的差异
ID3 使用信息增益偏向特征值多的特征,C4.5 使用信息增益率克服信息增益的缺点,偏向于特征值小的特征,CART 使用基尼指数克服 C4.5 需要求 log 的巨大计算量,偏向于特征值较多的特征。
使用场景的差异
ID3 和 C4.5 都只能用于分类问题,CART 可以用于分类和回归问题;ID3 和 C4.5 是多叉树,速度较慢,CART 是二叉树,计算速度很快;
样本数据的差异
ID3 只能处理离散数据且对缺失值敏感,C4.5 和 CART 可以处理连续性数据且有多种方式处理缺失值;从样本量考虑的话,小样本建议 C4.5、大样本建议 CART。C4.5 处理过程中需对数据集进行多次扫描排序,处理成本耗时较高,而 CART 本身是一种大样本的统计方法,小样本处理下泛化误差较大 ;
样本特征的差异
ID3 和 C4.5 层级之间只使用一次特征,CART 可多次重复使用特征;
剪枝策略的差异
ID3 没有剪枝策略,C4.5 是通过悲观剪枝策略来修正树的准确性,而 CART 是通过代价复杂度剪枝。
参考:
欢迎关注个人公众号:DS数说











**粗体** _斜体_ [链接](http://example.com) `代码` - 列表 > 引用。你还可以使用@来通知其他用户。