第一题 爬楼梯
题目信息
解题思路
对于n阶台阶
每次的选择为一阶或者两阶
剩余的台阶数分别为n-1和n-2
我们只需要分别求出n-1和n-2分别有多少种方案
再将其相加,便得到了n阶台阶的方案
然而很可惜
运行的时间太长了,通过不了
思考一下这个思路
我们会发现
在求n阶的方案时,我们需要分别求n-1和n-2的方案
求n-1的方案时,我们需要求n-2和n-3的方案
如此
除了求n阶方案之外,每个方案都求了两遍以上
我们可以很明显的注意到
这个数列的本质实际为斐波那契数列
我们可以将其从递归调用转换为循环叠加
这样,
我们就得到了官解的第一种解法
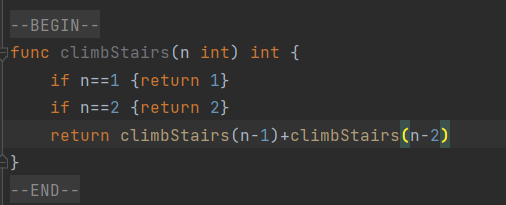
代码
func climbStairs(n int) int {
p, q, r := 0, 0, 1
for i := 1; i <= n; i++ {
p = q
q = r
r = p + q
}
return r
}
作者:LeetCode-Solution
链接:https://leetcode-cn.com/problems/climbing-stairs/solution/pa-lou-ti-by-leetcode-solution/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。复杂度分析
时间复杂度:循环执行 n 次,每次花费常数的时间代价,故渐进时间复杂度为 O(n)。
空间复杂度:这里只用了常数个变量作为辅助空间,故渐进空间复杂度为 O(1)。
优化
第二题 买卖股票的最佳时机
题目信息
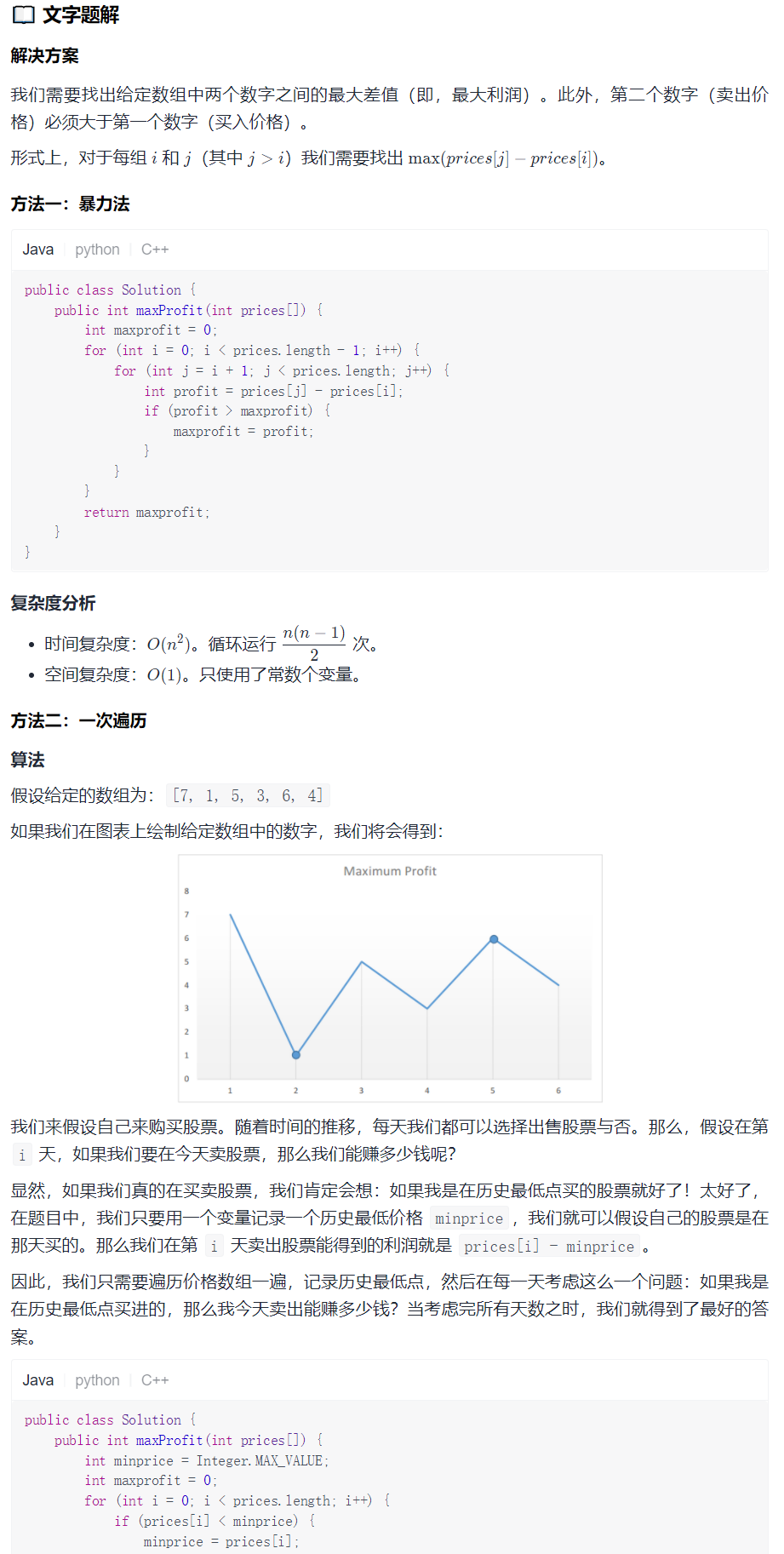
解题思路
代码
func maxProfit(prices []int) int {
minPrice :=10000
maxProfit :=0
for i:= 0; i < len(prices); i++ {
if prices[i] < minPrice {
minPrice = prices[i]
}else if (prices[i] - minPrice) > maxProfit {
maxProfit = prices[i] - minPrice
}
}
return maxProfit
}



**粗体** _斜体_ [链接](http://example.com) `代码` - 列表 > 引用。你还可以使用@来通知其他用户。