【golang】leetcode中级-最长子回文串&递增的三元子序列

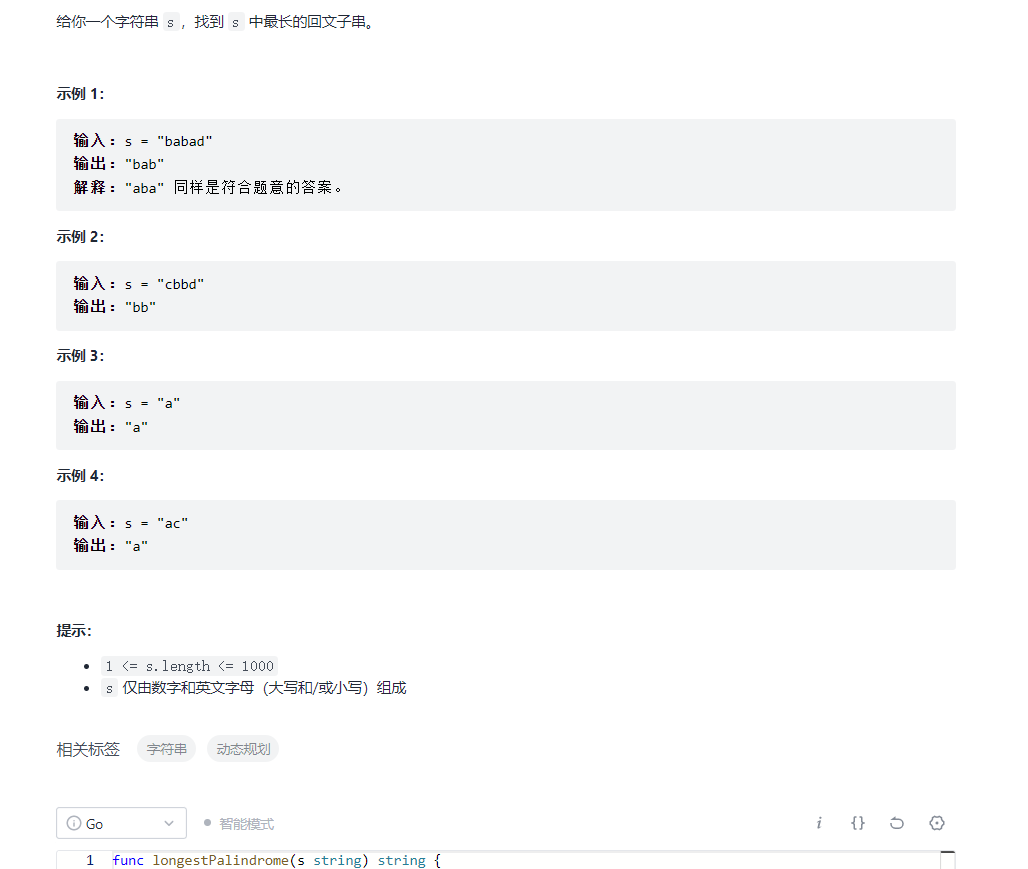
第一题 最长子回文串

题目

解题思路

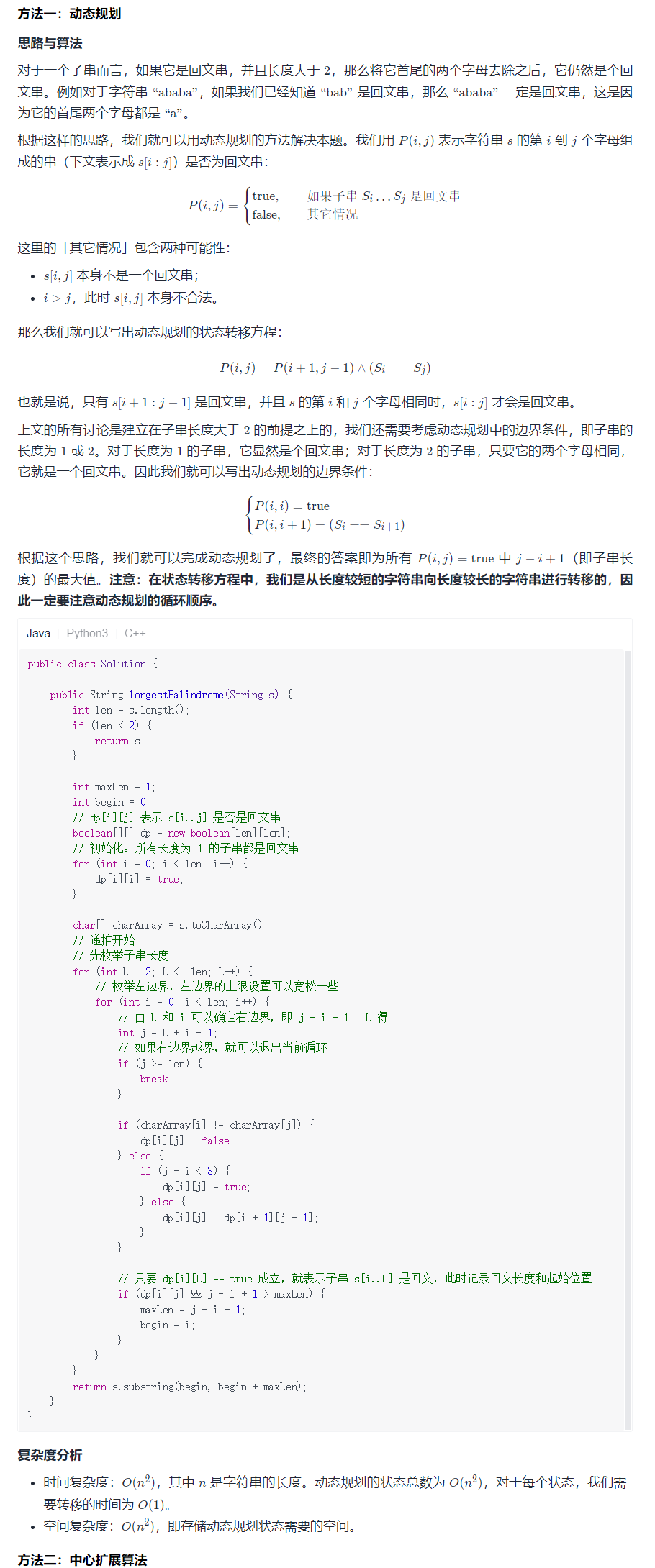
动态规划

其中 golang的二维数组切片初始化见如下
https://studygolang.com/artic...

详细代码

func longestPalindrome(s string) string {
    dp := make([][]bool, len(s))
    for i := 0; i < len(s); i++ {
        dp[i] = make([]bool, len(s))
    }
    ans := ""
    for i := 0; i < len(s); i++ {
        for k := 0; k <= i; k++ {
            dp[i][k] = s[i] == s[k] && (i-1 < k+1 || dp[i-1][k+1])
            if dp[i][k] && i-k+1 > len(ans) {
                ans = s[k : i+1]
            }
        }
    }
    return ans
}

作者：lllxxx
链接：https://leetcode-cn.com/problems/longest-palindromic-substring/solution/dong-tai-gui-hua-zui-jian-dan-xie-fa-by-6qd36/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

中心扩展算法

func longestPalindrome(s string) string {
    if s == "" {
        return ""
    }
    start, end := 0, 0
    for i := 0; i < len(s); i++ {
        //奇数
        left1, right1 := expandAroundCenter(s, i, i)
        //偶数
        left2, right2 := expandAroundCenter(s, i, i + 1)
        //start和end保存搜索到的最大回文串
        if right1 - left1 > end - start {
            start, end = left1, right1
        }
        if right2 - left2 > end - start {
            start, end = left2, right2
        }
    }
    return s[start:end+1]
}
//以当前left和right指向的字符串为中心向两边扩展，直到字符串不符合回文串为止停止拓展
//即搜索以left和right为中心的字符串的最大回文串
func expandAroundCenter(s string, left, right int) (int, int) {
    for ; left >= 0 && right < len(s) && s[left] == s[right]; left, right = left-1 , right+1 { }
    return left + 1, right - 1
}

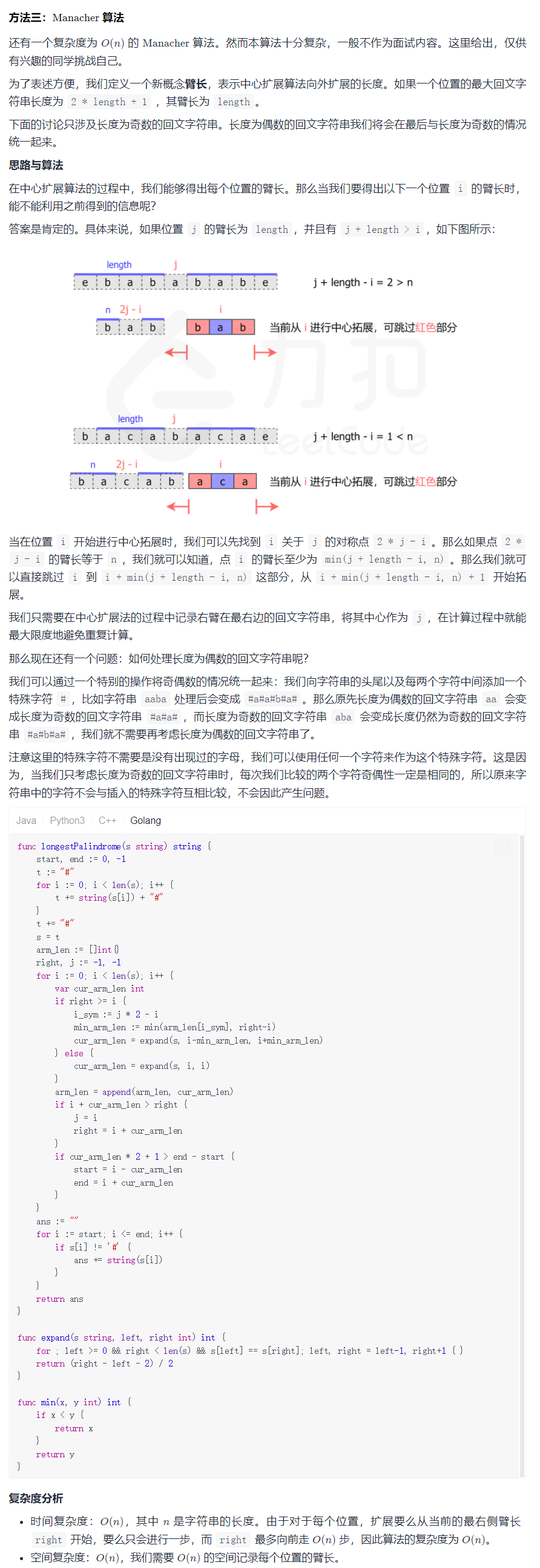
拓展 Manacher 算法

此解法在本题中并没有比解法二更为高效，仅供参考

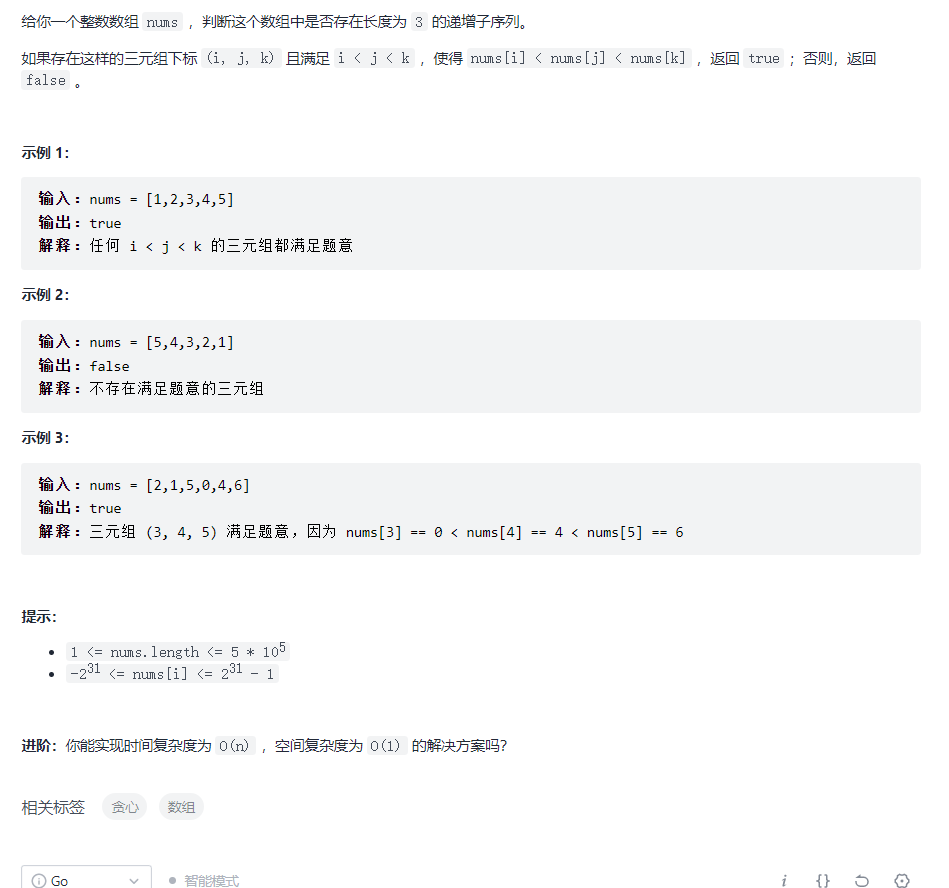
第二题 递增的三元子序列

题目

解题思路

实现过程

详细代码

func increasingTriplet(nums []int) bool {
    n := len(nums)
    if n < 3 {
        return false
    }
    first, second := nums[0], math.MaxInt32
    for i := 1; i < n; i++ {
        num := nums[i]
        if num > second {
            return true
        } else if num > first {
            second = num
        } else {
            first = num
        }
    }
    return false
}

复杂度分析

复杂度分析

时间复杂度：O(n)，其中 n 是数组 nums 的长度。需要遍历数组一次。

空间复杂度：O(1)。