第一题 相交链表
题目
解题思路
哈希查找
func getIntersectionNode(headA, headB *ListNode) *ListNode {
vis := map[*ListNode]bool{}
//将链表A的节点存入哈希表中
for tmp := headA; tmp != nil; tmp = tmp.Next {
vis[tmp] = true
}
//在哈希表中搜索链表B的第一个相同节点
for tmp := headB; tmp != nil; tmp = tmp.Next {
if vis[tmp] {
return tmp
}
}
return nil
}复杂度分析
时间复杂度:O(m+n),其中 m 和 n 是分别是链表 headA 和 headB 的长度。需要遍历两个链表各一次。
空间复杂度:O(m),其中 m 是链表 headA 的长度。需要使用哈希集合存储链表 headA 中的全部节点。
双指针
func getIntersectionNode(headA, headB *ListNode) *ListNode {
if headA == nil || headB == nil {
return nil
}
pa, pb := headA, headB
for pa != pb {//退出循环的条件为找到相同的节点或完成第二遍遍历,两者皆为空
if pa == nil {
pa = headB
} else {
pa = pa.Next
}
if pb == nil {
pb = headA
} else {
pb = pb.Next
}
}
return pa
}复杂度分析
时间复杂度:O(m+n),其中 m 和 n 是分别是链表 headA 和 headB 的长度。两个指针同时遍历两个链表,每个指针遍历两个链表各一次。
空间复杂度:O(1)。
另一种思路
func getIntersectionNode(headA, headB *ListNode) *ListNode {
// 判断谁更长,长多少
la, lb := length(headA), length(headB)
first, last, diff := headA, headB, la-lb
if la < lb {
first, last, diff = last, first, lb-la
}
// 长的先走
for i := 0; i < diff; i++ {
first = first.Next
}
// 一起往前走
for first != nil {
if first == last {
return first
}
first = first.Next
last = last.Next
}
return nil
}
func length(head *ListNode) (i int) {
for head != nil {
i++
head = head.Next
}
return
}
作者:arranger-core
链接:https://leetcode-cn.com/problems/intersection-of-two-linked-lists/solution/go-chang-gui-si-lu-dui-qi-qi-dian-by-huweicai/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。复杂度分析
时间复杂度:O(m+n+l),其中 m 和 n 是分别是链表 headA 和 headB 的长度。获取链表长度需要对链表进行遍历。l 为较长链表到相同节点的长度,最坏情况即无相同节点时也需遍历整个链表。
空间复杂度:O(1)。
第二题 二叉树的中序遍历
题目
解题思路
递归
对于深搜 递归调用函数对子树进行操作自然是最简单的解法
用函数值使代码更为简洁易懂
func inorderTraversal(root *TreeNode) (res []int) {
//将变量 inorder 声明为 func() 类型,此时 inorder 就被俗称为“回调函数”,此时 inorder 的值为 nil。
var inorder func(node *TreeNode)
//函数值
inorder = func(node *TreeNode) {
if node == nil {
return
}
左根右中序遍历
inorder(node.Left)
res = append(res, node.Val)
inorder(node.Right)
}
//对根节点进行操作
inorder(root)
return
}迭代
func inorderTraversal(root *TreeNode) (res []int) {
stack := []*TreeNode{}
for root != nil || len(stack) > 0 {
for root != nil {
stack = append(stack, root)
root = root.Left
}
root = stack[len(stack)-1]
stack = stack[:len(stack)-1]
res = append(res, root.Val)
root = root.Right
}
return
}
作者:LeetCode-Solution
链接:https://leetcode-cn.com/problems/binary-tree-inorder-traversal/solution/er-cha-shu-de-zhong-xu-bian-li-by-leetcode-solutio/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。详细过程见官解视频,
复杂度分析
时间复杂度:O(n),其中 n 为二叉树节点的个数。二叉树的遍历中每个节点会被访问一次且只会被访问一次。
空间复杂度:O(n)。空间复杂度取决于递归的栈深度,而栈深度在二叉树为一条链的情况下会达到 O(n) 的级别。
Morris 中序遍历
将左子树的最后一个节点连接到根节点上成为他的前缀,这样便可在遍历的时候一口气完成对树的遍历而不需要维护栈,降低了空间复杂度
func inorderTraversal(root *TreeNode) (res []int) {
for root != nil {
if root.Left != nil {
// predecessor 节点表示当前 root 节点向左走一步,然后一直向右走至无法走为止的节点
predecessor := root.Left
for predecessor.Right != nil && predecessor.Right != root {
// 有右子树且没有设置过指向 root,则继续向右走
predecessor = predecessor.Right
}
if predecessor.Right == nil {
// 将 predecessor 的右指针指向 root,这样后面遍历完左子树 root.Left 后,就能通过这个指向回到 root
predecessor.Right = root
// 遍历左子树
root = root.Left
} else { // predecessor 的右指针已经指向了 root,则表示左子树 root.Left 已经访问完了
res = append(res, root.Val)
// 恢复原样
predecessor.Right = nil
// 遍历右子树
root = root.Right
}
} else { // 没有左子树
res = append(res, root.Val)
// 若有右子树,则遍历右子树
// 若没有右子树,则整颗左子树已遍历完,root 会通过之前设置的指向回到这颗子树的父节点
root = root.Right
}
}
return
}
作者:LeetCode-Solution
链接:https://leetcode-cn.com/problems/binary-tree-inorder-traversal/solution/er-cha-shu-de-zhong-xu-bian-li-by-leetcode-solutio/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。复杂度分析
时间复杂度:O(n),其中 n 为二叉搜索树的节点个数。Morris 遍历中每个节点会被访问两次,因此总时间复杂度为 O(2n)=O(n)。
空间复杂度:O(1)



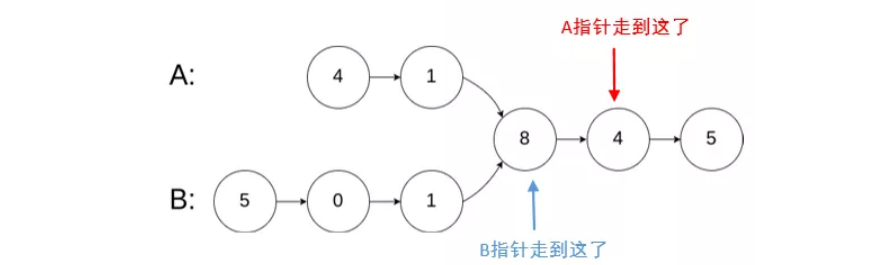
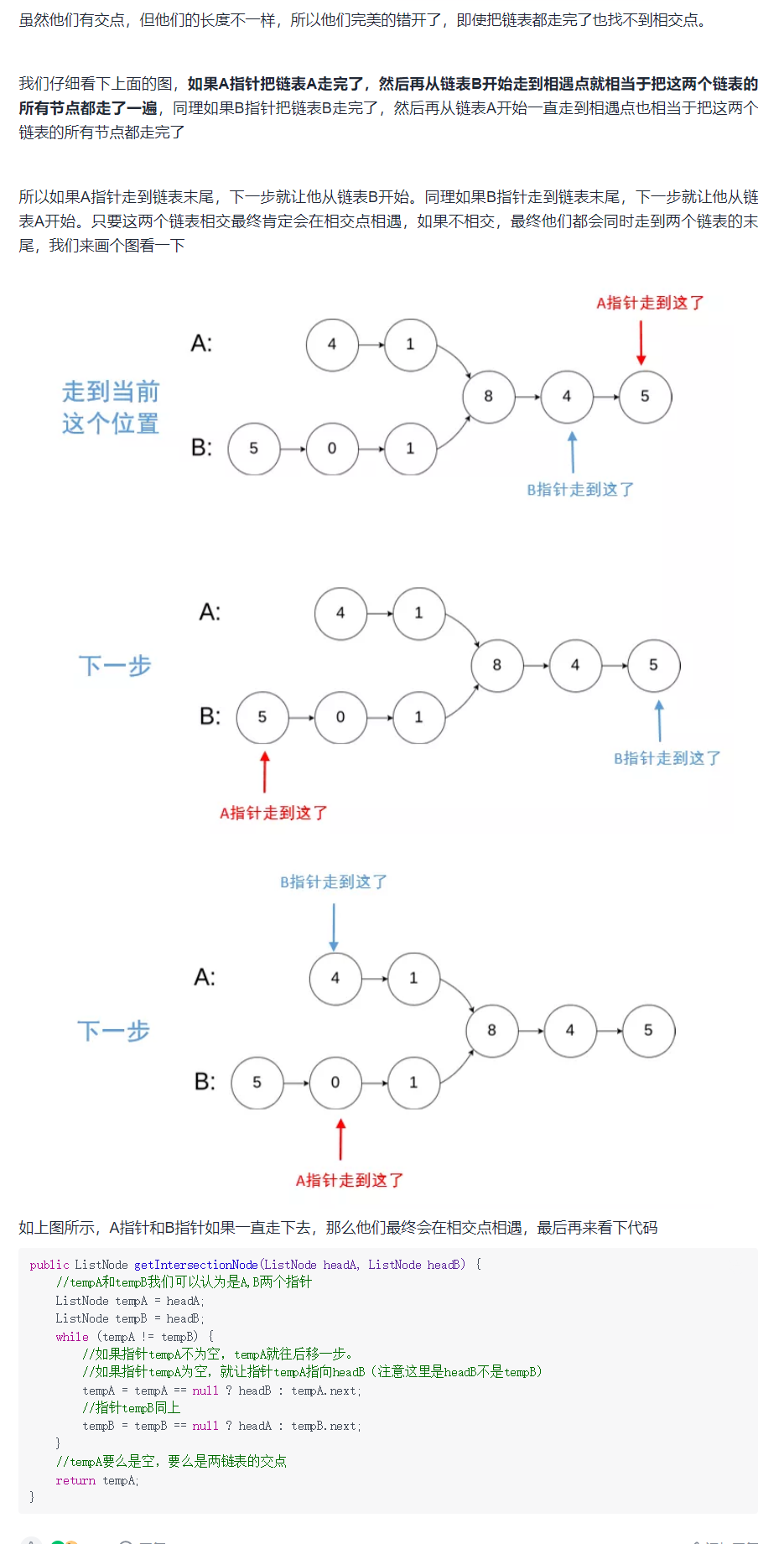







**粗体** _斜体_ [链接](http://example.com) `代码` - 列表 > 引用。你还可以使用@来通知其他用户。