【golang】leetcode中级-颜色分类&前K个高频元素

第一题 颜色分类

题目

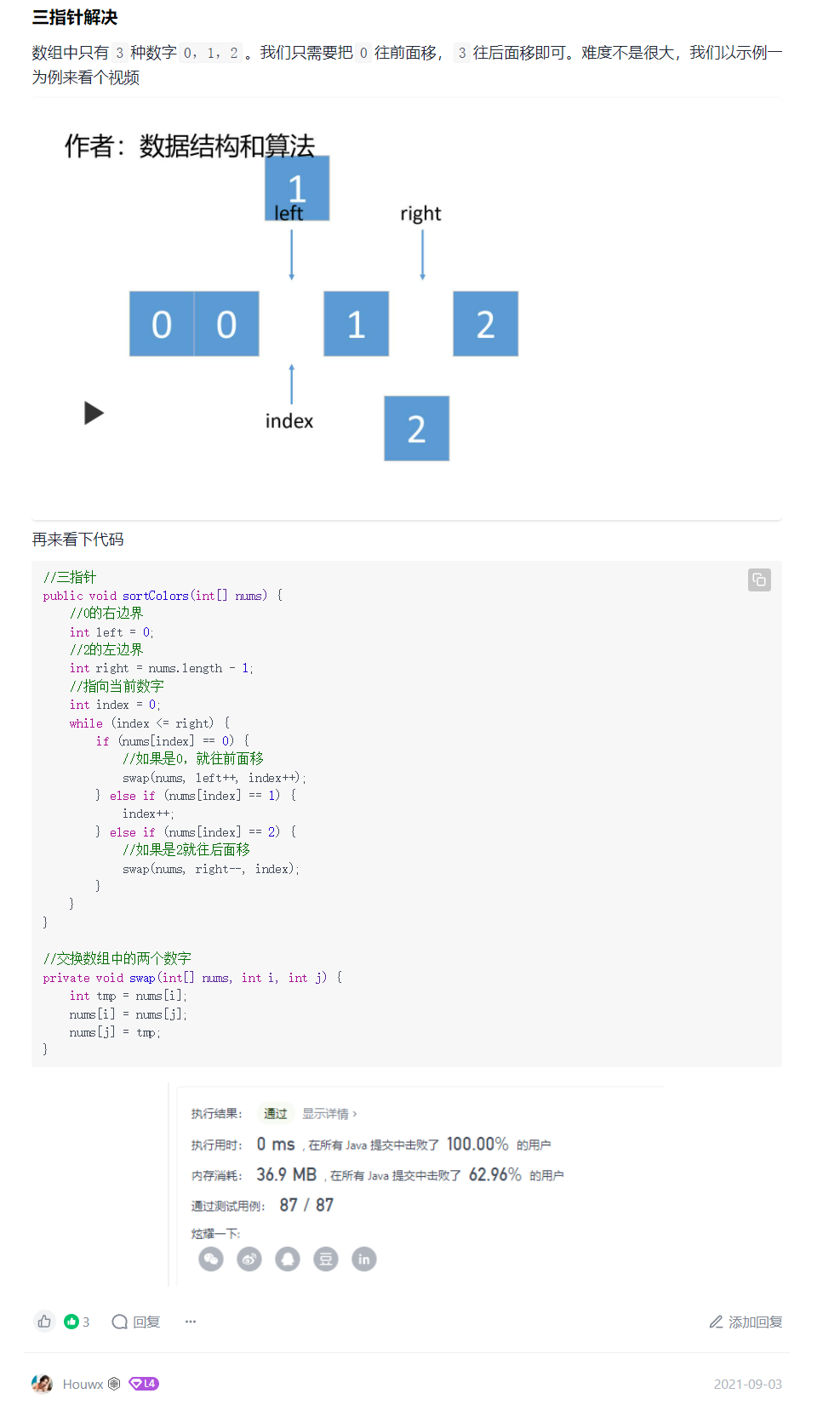
解题思路

代码

//三指针
func sortColors(nums []int)  {
    //0的右边界
    left := 0
    //2的左边界
    right := len(nums) - 1
    //指向当前数字
    index := 0
    for index <= right {
        if nums[index] == 0 {
            //如果是0，就往前面移
            swap(nums, left, index)
            left++
            index++
        } else if nums[index] == 1 {
            index++
        } else if nums[index] == 2 {
            //如果是2就往后面移
            swap(nums, right, index)
            right--
        }
    }
}
//交换数组中的两个数字
func swap(nums []int, i int, j int) {
    nums[i], nums[j]= nums[j],nums[i]
}

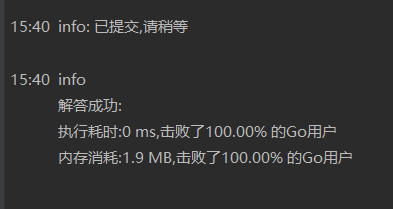
结果如下

复杂度分析

复杂度分析

时间复杂度：O(n)，其中 n 是数组 nums 的长度，index指针遍历0和1元素的长度，最坏结果为数组长度

空间复杂度：O(1)。三个指针，常数级别的空间复杂度

第二题 前 K 个高频元素

题目

解题思路

哈希表存储次数

代码

func topKFrequent(nums []int, k int) []int {
    m:=make(map[int]int)
    var res []int
    for _,n:=range nums{
        m[n]++
    }
    for i:=0;i<k;i++ {
        res=append(res,0)
        f:=0
        for n, v := range m {
            if v > f {
                res[i]=n
                f=v
            }
        }
        m[res[i]]=-1
    }
    return res
}

用时太长
继续优化

堆

这里引入堆的概念

代码

func topKFrequent(nums []int, k int) []int {
    occurrences := map[int]int{}
    for _, num := range nums {
        occurrences[num]++
    }
    h := &IHeap{}
    heap.Init(h)
    for key, value := range occurrences {
        heap.Push(h, [2]int{key, value})
        if h.Len() > k {
            heap.Pop(h)
        }
    }
    ret := make([]int, k)
    for i := 0; i < k; i++ {
        ret[k - i - 1] = heap.Pop(h).([2]int)[0]
    }
    return ret
}

type IHeap [][2]int

func (h IHeap) Len() int           { return len(h) }
func (h IHeap) Less(i, j int) bool { return h[i][1] < h[j][1] }
func (h IHeap) Swap(i, j int)      { h[i], h[j] = h[j], h[i] }

func (h *IHeap) Push(x interface{}) {
    *h = append(*h, x.([2]int))
}

func (h *IHeap) Pop() interface{} {
    old := *h
    n := len(old)
    x := old[n-1]
    *h = old[0 : n-1]
    return x
}

作者：LeetCode-Solution
链接：https://leetcode-cn.com/problems/top-k-frequent-elements/solution/qian-k-ge-gao-pin-yuan-su-by-leetcode-solution/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

复杂度分析
时间复杂度：O(Nlogk)，其中 N 为数组的长度。我们首先遍历原数组，并使用哈希表记录出现次数，每个元素需要 O(1) 的时间，共需 O(N) 的时间。随后，我们遍历「出现次数数组」，由于堆的大小至多为 k，因此每次堆操作需要 O(logk) 的时间，共需 O(Nlogk) 的时间。二者之和为 O(Nlogk)。
空间复杂度：O(N)。哈希表的大小为 O(N)，而堆的大小为 O(k)，共计为 O(N)。

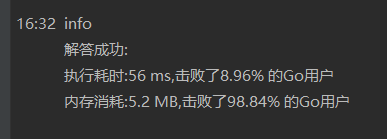
执行时间得到了大幅度优化

基于快速排序

代码

func topKFrequent(nums []int, k int) []int {
    occurrences := map[int]int{}
    for _, num := range nums {
        occurrences[num]++
    }
    values := [][]int{}
    for key, value := range occurrences {
        values = append(values, []int{key, value})
    }
    ret := make([]int, k)
    qsort(values, 0, len(values) - 1, ret, 0, k)
    return ret
}

func qsort(values [][]int, start, end int, ret []int, retIndex, k int) {
    rand.Seed(time.Now().UnixNano())
    picked := rand.Int() % (end - start + 1) + start;
    values[picked], values[start] = values[start], values[picked]

    pivot := values[start][1]
    index := start

    for i := start + 1; i <= end; i++ {
        if values[i][1] >= pivot {
            values[index + 1], values[i] = values[i], values[index + 1]
            index++
        }
    }
    values[start], values[index] = values[index], values[start]
    if k <= index - start {
        qsort(values, start, index - 1, ret, retIndex, k)
    } else {
        for i := start; i <= index; i++ {
            ret[retIndex] = values[i][0]
            retIndex++
        }
        if k > index - start + 1 {
            qsort(values, index + 1, end, ret, retIndex, k - (index - start + 1))
        }
    }
}

作者：LeetCode-Solution
链接：https://leetcode-cn.com/problems/top-k-frequent-elements/solution/qian-k-ge-gao-pin-yuan-su-by-leetcode-solution/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

复杂度分析

时间复杂度：O(N^2)，其中 N 为数组的长度。
设处理长度为 N 的数组的时间复杂度为 f(N)。由于处理的过程包括一次遍历和一次子分支的递归，最好情况下，有 f(N)=O(N)+f(N/2)，根据 主定理 ，能够得到 f(N)=O(N)。
最坏情况下，每次取的中枢数组的元素都位于数组的两端，时间复杂度退化为 O(N^2)。但由于我们在每次递归的开始会先随机选取中枢元素，故出现最坏情况的概率很低。
平均情况下，时间复杂度为 O(N)。
空间复杂度：O(N)。哈希表的大小为 O(N)，用于排序的数组的大小也为 O(N)，快速排序的空间复杂度最好情况为O(logN)，最坏情况为 O(N)。