贝叶斯网络的D-separation详解和Python代码实现

D分离（D-Separation）又被称作有向分离，是一种用来判断变量是否条件独立的图形化方法。相比于非图形化方法，D-Separation更加直观且计算简单。对于一个DAG（有向无环图），D-Separation方法可以快速的判断出两个节点之间是否是条件独立的。

了解 D 分离

在贝叶斯网络中，D 分离到底是什么，它可以用于什么？简单地说，它是一种常规的确定独立性的方法。如果两个变量X 和 Y 在有向图中相对于另外一组变量 Z 是 d 分离的，那么在这种图可以表示的所有概率分布中都是独立于 Z 的。这是什么意思？这意味着两个变量X和Y在Z上是独立的，如果一旦你知道了Z，那么关于X的知识是不会给你关于Y的任何额外信息的。

要完全理解它是如何完成的，首先需要介绍 active 和 inactive trails 。如果一条路径存在依赖关系，就可以说它是 active。例如，两个变量 X 和 Y 可能通过图中的多个路径连接。如果没有任何路径处于active状态，则 X 和 Y 是 d 分隔的。让我们看一下四种不同的情况，并确定那些是处于active 状态：

，Case1：在这种情况下，我们相信X可以通过Z来影响Y。但是如果观察到Z，X不会通过Z影响Y，因为Z已知。

Case2：这种情况与上面是对称的：如果观察到Z，X不能通过Z影响Y，但是如果没有观察到Z，X可以通过Z影响Y。

Case3：当且仅当Z没有被观察到时，X可以通过Z影响Y

Case4：如果Z没有被观察到，X就不能影响Y。这也被称为v形结构。

所有这些分析可以用以下方式总结：

可达性分析(RA)算法

我们现在可以考虑另一种算法，所谓的可达算法（Reachable Algorithm），它用于从给定Z的active路径寻找X可达的节点。算法由:

为了一步一步地理解算法。从算法的输入开始：

输入很好理解，然后该算法将返回从 X 可到达的所有节点。这部分是通过两个阶段来实现的：

• 阶段 1：这是算法的简单部分——找到 Z 中包含的所有节点的祖先。
• 阶段 2：从 X 开始，找到可达节点——哪些节点可以直接从 X 到达，然后哪些节点可以从这些节点到达。然后循环这个过程。

为了将这个步骤可视化，假设有一个一下的贝叶斯网络：

可以从解决这个问题开始：

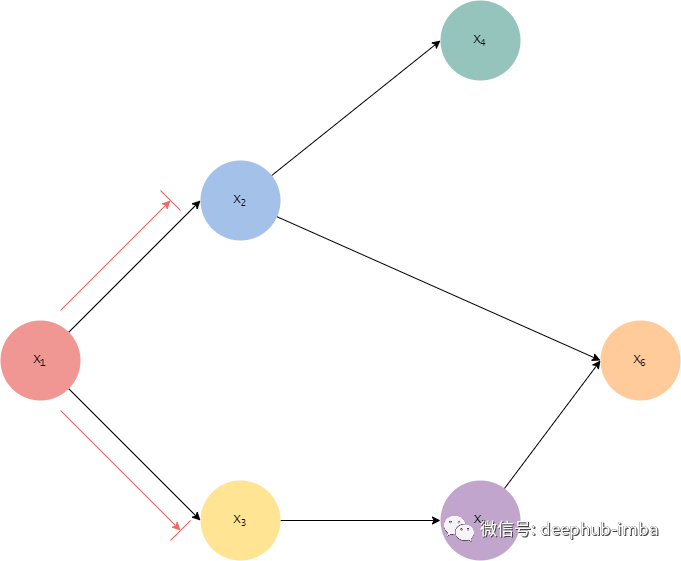
这就相当于给出 X_2 和 X_3 来让我们确认是否有从 X_1 到 X_6 的active trails。算法从寻找X_2 和 X_3 的祖先开始，可以看到除X_1 之外它们没有任何祖先。因此变量A如下：

现在进入第2阶段——检查不同的active trails。因为问题是检查X_1和 X_6之间是否有active trails，所以这里从X_1开始:

这对应于上面的Case 1 或 2，这不是active trails。如果再看另一条线索：

这也对应于Case 1 或 2。因此，我们在 X_1 和 X_6 之间没有active trails，它们是 d 分离的。可以直观地展示这一点：

现在再次考虑相同的贝叶斯网络，但查看以下问题：

这与上面的通过给出 X_1 和 X_6 来询问我们是否有从 X_2 到 X_3 的active trails相同。算法从查找 X_1 和 X_6 的祖先开始，它们需要插入到变量 A 中：

进入第 2 阶段，尝试从 X_2 开始，并从考虑路径开始：

找到了 X_6，这意味着这对应于Case 4。因此可以看到它是一个active trails。然后我们可以继续以下路径：

这也是一条active trail——因为在给定 X_1 和 X_6 的情况下找到了一条从 X_2 到 X_3 的active trail。现在，是否有可能从另一个方法做到这一点？换句话说，是否可以这样做：

它将等于Case 3，因为得到了 X_1——因此，它不是一个active trail：

D 分离的另一种算法

还有一种比较常见的D分离算法：

• 绘制祖先图，绘制仅包含提到的变量及其所有祖先的网络的简化版。
• 连接节点的父节点，为具有共同子节点的变量之间绘制一条无向边。
• 将有向边替换为无向边
• 删除给定节点及其边：例如，在“给定 Z 的情况下，X 和 Y 是否独立？”，则必须删除 Z 及其所有边。
• 分析这个简化的图，如果图中的变量不相连，则它们是独立的。如果变量 阅读图表——，则不能保证它们是独立的。

下面使用以下的图进行算法的说明：

现在确认以下问题：

可视化说明这个过程：

可以看到它们仍然是连接的，这意味着 A 和 B 在给定 C 的情况下不是条件独立的。

再看看另一个问题：

最后得到的结果如下：

没有连接，这意味着 A 和 B 是独立的。

最后一个例子：

结果如下：

可以看到 D 和 E 通过一条通过 C 的路径相连，因此在给定 A 和 B 的情况下，它们显然是条件独立的。

概念已经介绍完毕了，现在看看如何使用 Python 来实现它。

Python代码实现

实现图结构

要使用该算法，首先需要有一个图作为处理的数据。 导入需要的库：

实现结构时首先需要能够访问图的边和节点。由于它是有向图，因此能够访问图中所有节点的父节点和子节点也很有用。此外还需要一个可以可视化图的函数：

实现 D 分离算法

现在可以编写 D 分离算法的代码了。

阶段 1，简单地找到给定节点的所有祖先——这里给定节点包括开始节点、结束节点和我们条件的节点。

阶段2 ，我们从起始节点搜索所有可能的inactive trails。代码如下：

算法的目标是执行如下的查询：

所以需要扩展上面给出的代码。上面的代码已经从起始节点找到了所有可能的活动路径——然后只需要检查结束节点是否包含在这个列表中就可以了。最后还可以对不同节点进行颜色编码的网络可视化。代码如下：

现在看看代码是否有效。假设有一个贝叶斯网络，如下所示：

我们来确认：

Are node 4 and 5 d-separated given node 6?

总结

在本文中介绍了 D 分离的概念及其相应的算法，并且使用 Python实现了该算法，虽然代码中还有很多可以优化的地方，但是这对于我们理解算法是一个非常好帮助，最后在实践中使用我们编写的代码进行了实验，证明代码是没有问题的。

引用：

• Koller, D., & Friedman, N. (2009). Probabilistic Graphical Models: Principles and Techniques (1st ed.). The MIT Press.
• Ermon, S. (2022). Bayesian networks. Github. https://ermongroup.github.io/...
• https://www.overfit.cn/post/7247991e27a74d7da6ae97c87a89eb6f

作者：Naja Møgeltoft