The application of linear algebra in the front end (2): realize the mouse dragging and rotating elements, Canvas graphics

Introduction

Seeing the title of the article, many students may be confused. To realize the rotation of an element, you only need to obtain the rotation angle, and then use the CSS transform:rotate(${rotation angle}deg) in to achieve the rotation requirement. Why? Use knowledge of linear algebra?

I think the reasons for using the knowledge of linear algebra to achieve element drag and rotation are as follows:

• The matrix can contain rotation, scaling, translation and other information at the same time, without redundant calculation and attribute update;
• more general. The knowledge of linear algebra is a kind of mathematical knowledge, which is abstract and general. Many GUI programming techniques provide linear algebra matrix to achieve element rotation, Canvas , translation and matrix() transform CSS The setTransform() , etc. API , Android Canvas class provides the setMatrix() method. Learn linear algebra matrix rotation, you can take all such requirements in each GUI programming technology.

Principle Analysis of Drag and Rotation

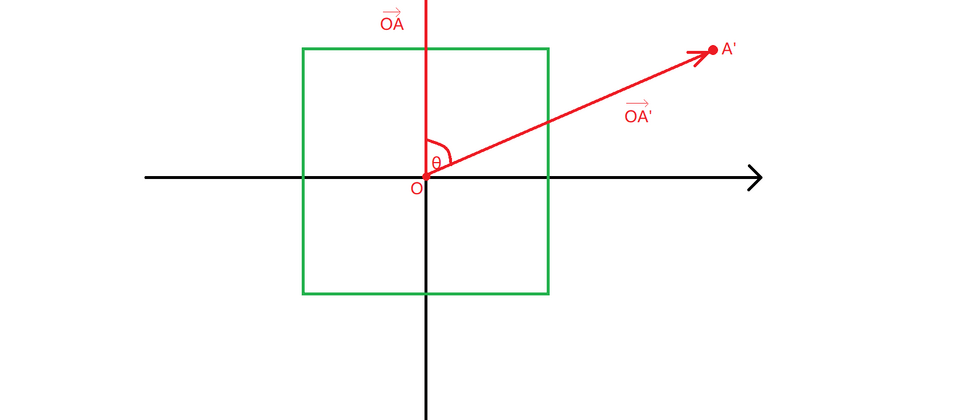
A drag rotation is essentially a rotation around the origin, which is the center of the object. Let us use a rectangle to abstractly express this rotation process, take the center of the rectangle as the origin\(O\), establish a \(2D\) coordinate system, take a point as the rotation start point\(A\), take a point as the rotation end point \(A'\), connect \(A\), \(A'\) and \(O\) to get vector\(\overrightarrow{OA}\), vector\(\overrightarrow{OA'} \), the angle between the vector\(\overrightarrow{OA}\) and the vector\(\overrightarrow{OA'}\)\(\theta\), the following figure can be obtained:

In JavaScript, the Math.atan2() API can return the plane angle (radian value) between the line segment from \(origin (0,0)\) to \((x,y) point\) and the positive direction of \(x axis\), So the code to find the angle between two vectors in radians is as follows:

/**
 * 计算向量夹角，单位是弧度
 * @param {Array.<2>} av 
 * @param {Array.<2>} bv 
 * @returns {number}
 */
    function computedIncludedAngle(av, bv) {
        return Math.atan2(av[1], av[0]) - Math.atan2(bv[1], bv[0]);
    }

rotation matrix

In the previous application of linear algebra in the front end (1): realizing the mouse wheel zoom element, Canvas picture and dragging , we know that the zoom element can use the zoom matrix, then the rotation element can also use the rotation matrix, then How to derive the rotation matrix becomes the key. Since we only care about the rotation in the plane dimension, we only need to obtain the rotation matrix in the \(2D\) dimension.

Assuming that there are base vectors \(p\) and base vectors \(q\) parallel to \(X axis\) and \(Y axis\) in the \(2D\) coordinate axis, the angle between them is For \(90^{\circ}\), rotate the basis vector\(p\) and the basis vector\(q\) at the same time\(\theta degree\), you can get the basis vector\(p'\) and the basis Vector \(q'\), the value of \(p\), \(p'\) can be deduced according to \(trigonometric function\).

Using the basis vector to construct the matrix, the \(2D\) rotation matrix is as follows:

$$ R(\theta)=\left[ \begin{matrix} p^{'} \\ q^{'} \\ \end{matrix} \right]=\left[ \begin{matrix} cos\theta & sin\theta \\ -sin\theta & cos\theta \end{matrix} \right] $$

Converted to \(4\times4 homogeneous matrix\) is:

$$ R(\theta)=\left[ \begin{matrix} p^{'} \\ q^{'} \\ r^{'}\\ w^{'} \\ \end{matrix} \right]=\left[ \begin{matrix} cos\theta & sin\theta & 0 & 0 \\ -sin\theta & cos\theta & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{matrix} \right] $$

matrix() function to realize matrix change in CSS

CSS function matrix() specifies a 2D transformation matrix consisting of the specified 6 values.
matrix(a, b, c, d, tx, ty) is shorthand for matrix3d(a, b, 0, 0, c, d, 0, 0, 0, 0, 1, 0, tx, ty, 0, 1) .

These values represent the following functions:

matrix( scaleX(), skewY(), skewX(), scaleY(), translateX(), translateY() )

For example, if we want a div element to be doubled, panned horizontally to the right by 100px, and vertically panned down by 200px, we can write CSS as:

div {
    transform:matrix(2, 0, 0, 2, 100, 200);
}

Since we use \(4\times4 homogeneous matrix\) for matrix transformation calculation, we use homogeneous coordinates under \(RP^{3}\). It is worth noting that we can also write the following form about \(homogeneous coordinates\), which we will use in this article:

$$ \left[ \begin{matrix} a & c & 0 & 0 \\ b & d & 0 & 0 \\ 0 & 0 & 1 & 0 \\ tx & ty & 0 & 1 \end{matrix} \right] $$

Matrix calculation library gl-matrix

gl-matrix is an open source matrix computation library written in the JavaScript language. We can use the operation function between matrices provided by this library to simplify and speed up our development. In order to avoid reducing the complexity, the following uses the native ES6 syntax, uses the <script> tag to directly reference JS library, and does not introduce any front-end compilation toolchain.

Mouse drag to rotate Div element

Rotation effect

Code

index.html

<!DOCTYPE html>
<html lang="en">
<head>
    <meta charset="UTF-8">
    <meta http-equiv="X-UA-Compatible" content="IE=edge">
    <meta name="viewport" content="width=device-width, initial-scale=1.0">
    <title>矩阵旋转Div元素</title>
    <link rel="stylesheet" href="./index.css">
</head>
<body>
    <div class="shape_controls">
        <div class="shape_anchor"></div>
        <div class="shape_rotater"></div>
    </div>
    <script src="./gl-matrix-min.js"></script>
    <script src="./index.js"></script>
</body>
</html>

index.css

*,
*::before,
*::after {
    box-sizing: border-box;
}

body {
    position: relative;
    margin: 0;
    padding: 0;
    min-height: 100vh;
}

.shape_controls {
    position: absolute;
    left: 50%;
    top: 50%;
    transform: translate(-50%, -50%);
    width: 200px;
    height: 200px;
    border: 1px solid rgb(0, 0, 0);
    z-index: 1;
}

.shape_controls .shape_anchor {
    position: absolute;
    left: 50%;
    top: 0%;
    transform: translate(-50%, -50%);
    width: 8px;
    height: 8px;
    border: 1px solid rgb(6, 123, 239);
    border-radius: 50%;
    background-color: rgb(255, 255, 255);
    z-index: 2;
}

.shape_controls .shape_rotater {
    position: absolute;
    left: 50%;
    top: -30px;
    transform: translate(-50%, 0);
    width: 8px;
    height: 8px;
    border: 1px solid rgb(6, 123, 239);
    border-radius: 50%;
    background-color: rgb(255, 255, 255);
    z-index: 2;
}

.shape_controls .shape_rotater:hover {
    cursor: url(./rotate.gif) 16 16, auto;
}

.shape_controls .shape_rotater::after {
    position: absolute;
    content: "";
    left: 50%;
    top: calc(100% + 1px);
    transform: translate(-50%, 0);
    height: 18px;
    width: 1px;
    background-color: rgb(6, 123, 239);
}

rotate.gif

index.js

document.addEventListener("DOMContentLoaded", () => {
    const $sct = document.querySelector(".shape_controls");
    const $srt = document.querySelector(".shape_controls .shape_rotater");
    const {left, top, width, height} = $sct.getBoundingClientRect();
    // 原点坐标
    const origin = [left + width / 2 , top + height / 2];
    // 是否旋转中
    let rotating = false;
    // 旋转矩阵
    let prevRotateMatrix = getElementTranformMatrix($sct);
    let aVector = null;
    let bVector = null;

    /**
     * 获取元素的变换矩阵
     * @param {HTMLElement} el 元素对象
     * @returns {Array.<16>} 
     */
    function getElementTranformMatrix(el) {
        const matrix = getComputedStyle(el)
                        .transform
                        .replace("matrix(", "")
                        .replace(")", "")
                        .split(",")
                        .map(item => parseFloat(item.trim()));
        return new Float32Array([
            matrix[0], matrix[2], 0, 0,
            matrix[1], matrix[3], 0, 0,
            0, 0, 1, 0,
            matrix[4], matrix[5], 0, 1
        ]);
    }

    /**
     * 给元素设置变换矩阵
     * @param {HTMLElement} el 元素对象
     * @param {Array.<16>} hcm 齐次坐标4x4矩阵 
     */
    function setElementTranformMatrix(el, hcm) {
        el.setAttribute("style", `transform: matrix(${hcm[0]} ,${hcm[4]}, ${hcm[1]}, ${hcm[5]}, ${hcm[12]}, ${hcm[13]});`);
    }

    /**
     * 计算向量夹角，单位是弧度
     * @param {Array.<2>} av 
     * @param {Array.<2>} bv 
     * @returns {number}
     */
    function computedIncludedAngle(av, bv) {
        return Math.atan2(av[1], av[0]) - Math.atan2(bv[1], bv[0]);
    }

    // 监听元素的点击事件，如果点击了旋转圆圈，开始设置起始旋转向量
    $srt.addEventListener("mousedown", (e) => {
        const {clientX, clientY} = e;
        rotating = true;
        aVector = [clientX - origin[0], clientY - origin[1]];
    });

    // 监听页面鼠标移动事件，如果处于旋转状态中，就计算出旋转矩阵，重新渲染
    document.addEventListener("mousemove", (e) => {
        // 如果不处于旋转状态，直接返回，避免不必要的无意义渲染
        if (!rotating) {
            return;
        }
        // 计算出当前坐标点与原点之间的向量
        const {clientX, clientY} = e;
        bVector = [clientX - origin[0], clientY - origin[1]];
        // 根据2个向量计算出旋转的弧度
        const angle  = computedIncludedAngle(aVector, bVector);

        const o = new Float32Array([
            0, 0, 0, 0,
            0, 0, 0, 0,
            0, 0, 0, 0,
            0, 0, 0, 0
        ]);
        // 旋转矩阵
        const rotateMatrix = new Float32Array([
            Math.cos(angle), Math.sin(angle), 0, 0,
            -Math.sin(angle), Math.cos(angle), 0, 0,
            0, 0, 1, 0,
            0, 0, 0, 1
        ]);
        // 把当前渲染矩阵根据旋转矩阵，进行矩阵变换，得到新矩阵
        prevRotateMatrix = glMatrix.mat4.multiply(o, prevRotateMatrix, rotateMatrix); 
        // 给元素设置变换矩阵，完成旋转
        setElementTranformMatrix($sct, prevRotateMatrix);
        aVector = bVector;
    });

    // 鼠标弹起后，移除旋转状态
    document.addEventListener("mouseup", () => {
        rotating = false;
    })    
});

Mouse drag to rotate Canvas graphics

Rotation effect

Code

index.html

<!DOCTYPE html>
<html lang="en">
<head>
    <meta charset="UTF-8">
    <meta http-equiv="X-UA-Compatible" content="IE=edge">
    <meta name="viewport" content="width=device-width, initial-scale=1.0">
    <title>矩阵旋转Canvas图形</title>
    <link rel="stylesheet" href="./index.css">
</head>
<body>
    <canvas id="app"></canvas>
    <script src="./gl-matrix-min.js"></script>
    <script src="./index.js"></script>
</body>
</html>

index.css

*,
*::before,
*::after {
    box-sizing: border-box;
}

body {
    margin: 0;
    padding: 0;
    overflow: hidden;
}

canvas {
    display: block;
}

.rotating,
.rotating div {
    cursor: url(./rotate.gif) 16 16, auto !important;
}

index.js

document.addEventListener("DOMContentLoaded", () => {
    const pageWidth = document.documentElement.clientWidth;
    const pageHeight = document.documentElement.clientHeight;
    const $app = document.querySelector("#app");
    const ctx = $app.getContext("2d");
    $app.width = pageWidth;
    $app.height = pageHeight;
    const width = 200;
    const height = 200;
    const cx = pageWidth / 2;
    const cy = pageHeight / 2;
    const x = cx - width / 2;
    const y = cy - height / 2;
    // 原点坐标
    const origin = [x + width / 2 , y + height / 2];
    // 是否旋转中
    let rotating = false;
    let aVector = null;
    let bVector = null;
    // 当前矩阵
    let currentMatrix = new Float32Array([
        1, 0, 0, 0,
        0, 1, 0, 0,
        0, 0, 1, 0,
        origin[0], origin[1], 0, 1
    ]);

    /**
     * 计算向量夹角，单位是弧度
     * @param {Array.<2>} av 
     * @param {Array.<2>} bv 
     * @returns {number}
     */
    function computedIncludedAngle(av, bv) {
        return Math.atan2(av[1], av[0]) - Math.atan2(bv[1], bv[0]);
    }

    /**
     * 渲染视图
     * @param {MouseEvent} e 鼠标对象 
     */
    function render(e) {
        // 清空画布内容
        ctx.clearRect(0, 0, ctx.canvas.width,  ctx.canvas.height);
        ctx.save();

        // 设置线段厚度，防止在高分屏下线段发虚的问题
        ctx.lineWidth = window.devicePixelRatio;

        // 设置变换矩阵
        ctx.setTransform(currentMatrix[0], currentMatrix[4], currentMatrix[1], currentMatrix[5], currentMatrix[12], currentMatrix[13]);
        
        // 绘制矩形
        ctx.strokeRect(-100, -100, 200, 200);

        // 设置圆圈的边框颜色和填充色
        ctx.fillStyle = "rgb(255, 255, 255)";
        ctx.strokeStyle = "rgb(6, 123, 239)";
    
        // 绘制矩形上边框中间的蓝色圆圈
        ctx.beginPath();
        ctx.arc(0, -100, 4, 0 , 2 * Math.PI);
        ctx.stroke();
        ctx.fill();

        // 绘制可以拖拽旋转的蓝色圆圈
        ctx.beginPath();
        ctx.arc(0, -130, 4, 0 , 2 * Math.PI);
        ctx.stroke();
        ctx.fill();

        // 判断是否拖拽旋转的蓝色圆圈
        const {pageX, pageY} = e ? e : {pageX: -99999, pageY: -9999};
        if (ctx.isPointInPath(pageX, pageY)) {
            rotating = true;
        }
        // 绘制链接两个圆圈的直线
        ctx.beginPath();
        ctx.fillStyle = "transparent";
        ctx.strokeStyle = "#000000";
        ctx.moveTo(0, -125);
        ctx.lineTo(0, -105);
        ctx.stroke();

        ctx.restore();
    }

    // 初次渲染
    render();

    // 监听画布的点击事件，如果点击了旋转圆圈，开始设置起始旋转向量
    $app.addEventListener("mousedown", (e) => {
        // 在渲染的过程中会判断是否点击了旋转圆圈，如果是，那么rotating会被设置为true
        render(e);
        if (!rotating) {
            return;
        }
        const { offsetX, offsetY } = e;
        aVector = [offsetX - origin[0], offsetY - origin[1]];
    });

    // 监听页面鼠标移动事件，如果处于旋转状态中，就计算出旋转矩阵，重新渲染
    document.addEventListener("mousemove", (e) => {
        // 如果不处于旋转状态，直接返回，避免不必要的无意义渲染
        if (!rotating) {
            return;
        }
        // 给画布添加旋转样式
        $app.classList.add("rotating");

        // 计算出当前坐标点与原点之间的向量
        const { offsetX, offsetY } = e;
        bVector = [offsetX - origin[0], offsetY - origin[1]];
        // 根据2个向量计算出旋转的弧度
        const angle = computedIncludedAngle(aVector, bVector);

        // 旋转矩阵
        const rotateMatrix = new Float32Array([
            Math.cos(angle), Math.sin(angle), 0, 0,
            -Math.sin(angle), Math.cos(angle), 0, 0,
            0, 0, 1, 0,
            0, 0, 0, 1
        ]);
        // 把当前渲染矩阵根据旋转矩阵，进行矩阵变换，得到画布的新渲染矩阵
        currentMatrix = glMatrix.mat4.multiply(
            glMatrix.mat4.create(),
            currentMatrix,
            rotateMatrix,
        );
        render(e);
        aVector = bVector;
    });

    // 鼠标弹起后，移除旋转状态
    document.addEventListener("mouseup", () => {    
        rotating = false;
        $app.classList.remove("rotating");
    });
});