Curve V1数学模型

curve，uniswap是Defi Developer的必学协议。在亮神的指导下我把白皮书和源码都过了一遍，但私底下还是要把最重要的部分整理一下。

背景

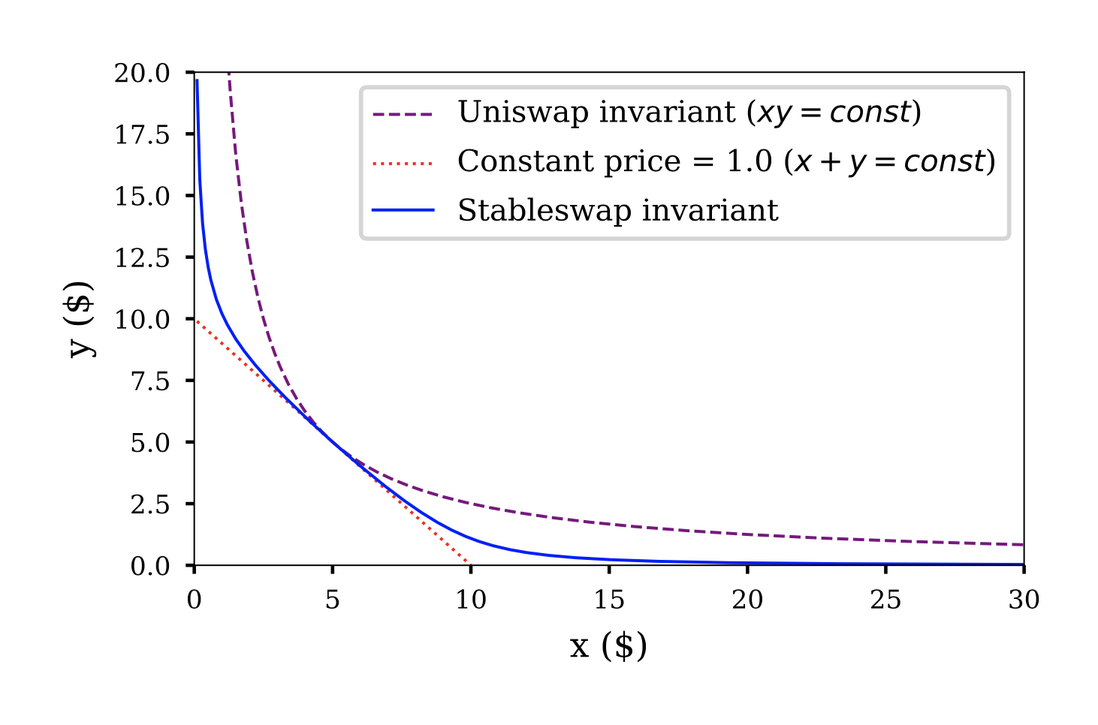
Curve V1要解决的问题就是稳定兑换问题。Uniswap V2的AMM公式xy=k的滑点太高了。Curve V1其实希望可以没有滑点1:1兑换。但是这个明显不太现实。如下图，红色虚线的 Constant Price是 x + y = const。紫色虚线就是 uniswap的AMM公式，xy=const。我们可以看到，红色线的兑换的价格滑点比紫色的小得多。所以，curve希望构建一个蓝色的曲线，“尽可能贴合”红色虚线。这就是curve的最核心的思想。

公式推导

假设在有n个组合的交易池中进行交易，考虑极端无滑点情况即永远1:1兑换,即存在守恒量

$$ \sum{x_i} = D $$

其中xi为第i个代币数量，所有代币数量和为常量。方便起见假设xi = D/n，考虑uniswap中存在滑点的常量积公式为
$$\prod{x_i} = (\frac{D}{n})^n$$

公式1是一种考虑极端无滑点的情况，可以理解为无穷杠杠；公式2是一种考虑了滑点的情况，等价于0杠杠。我们要去思考在两种极端的情况下取平衡。所以，设置了杠杠率X，让公式1和公式2进行线性加权。将以上两个极端情况进行线性组合成为适合稳定币的报价函数，组合系数选取为$$\chi{D^{n-1}}$$以满足量纲要求。最终得到
$$\chi{D^{n-1}}\sum{x_i} + \prod{x_i} = \chi{D^n} + (\frac{D}{n})^n$$

同时，如果上式始终成立，公式会依赖参数杠杠率X进行交易。 但是，参数X不支持远离理想价格 1.0 的价格。（上面的公式只支持当价格为$1的流动性支持）为了保证在任意价格都能提供流动性，这里取组合系数为变量，适当增加了交易数量对价格的影响。curve工程师们对参数X进行了函数定义：

$$ \chi = \frac{A\prod{x_i}}{{(D/n)}^n} $$

这里A为常数。由公式可知当每个代币数量均相等时$$\chi=A$$为常数，当不相等时$$\chi$$变小产生更多滑点，公式趋向amm形式。最终得到

$$ An^n\sum{x_i} + D = ADn^n + \frac{D^{n+1}}{n^n\prod{x_i}} $$

把上面的公式移项目就可以得到AMM的最终求根公式：

$$ y^{2}+\left(\frac{D}{A n^{n}}+\sum_{j \neq \text { out }} x_{j}^{\prime}-D\right) y-\frac{D^{n+1}}{A n^{2 n} \prod_{j \neq \text { out }} x_{j}^{\prime}}=0 $$

求解方法

虽然我们得到了上面的求根公式，但是实际代码里是用牛顿法来求解的：

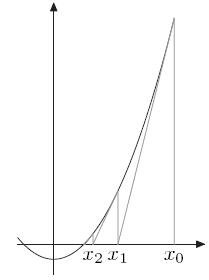
如图所示，不断在xi点做切线，其与横轴交点横坐标得x{i+1},通过这种不断迭代的方式逼近函数零点。迭代公式为
$$x_{i+1} = x_i-\frac{f(x_i)}{f'(x_i)}$$

最后

vyper这个语言跟python好像～～～