go算法实现：快排 quick sort

一、介绍

快排排序是由东尼·霍尔所发展的一种排序算法。在平均情况下，它的时间复杂度是Ο(nlogn)，在最坏的情况下是Ο(n2),不过这种情况不常见。
事实上，快速排序通常明显比其他 Ο(nlogn) 算法更快，因为它的内部循环（inner loop）可以在大部分的架构上很有效率地被实现出来，快排是最快的排序算法之一。
快速排序使用分治法（Divide and conquer）策略来把一个串行（list）分为两个子串行（sub-lists）。

二、算法步骤

1. 从数列中挑出一个元素，称为 "基准"（pivot）;
2. 重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区退出之后，该基准就处于数列的中间位置。这个称为分区（partition）操作；
3. 递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序；

三、算法代码实践

1.从数列中挑出一个元素，称为 "基准"（pivot）;
2.左边为小于"基准"的数据，右边为大于"基准"的数据，其中用到了分治的思想。
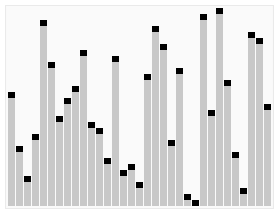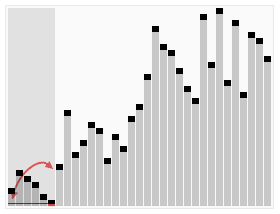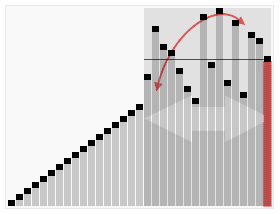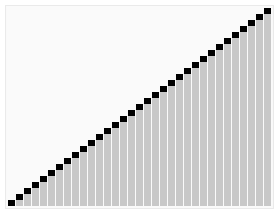
算法如下图所示：

其实从这张图我们也可以看出，快排的核心思路是：分治算法

//分治算法
func partition(n []int, left, right int) ([]int, int) {
    //1.基准点值，取最右边的值
    pivot := n[right]
    //2.新的基准点索引
    p := left
    for i := left; i < right; i++ {
        if n[i] < pivot {
            n[i], n[p] = n[p], n[i]
            p++
        }
    }
    //把pivot基准值，移动到新的 pivot基准点索引p上
    n[p], n[right] = n[right], n[p]
    return n, p
}

3.把每一个分治出来的数据，再进行递归

func quickSort(n []int, left, right int) []int {
    if left < right {
        var p int
        n, p = partition(n, left, right)
        quickSort(n, left, p-1)  //新基准版点p，左边再分区
        quickSort(n, p+1, right) //新基准版点p，右边再分区
    }
    return n
}

最后完整的quicSort快排，其实就是分治和递归的结合，如下面的动图。

写一个测试函数

func TestQuickSort(t *testing.T) {
    i := []int{6, 14, 37, 22, 8, 11, 45, 21, 9, 18, 30, 15, 19}
    t.Log(quickSort(i, 0, len(i)-1))
}

输出如下：

[6 8 9 11 14 15 18 19 21 22 30 37 45]

谢谢您的观看，欢迎关注我的公众号。