双指针的妙用——leetcode11盛最多水的容器

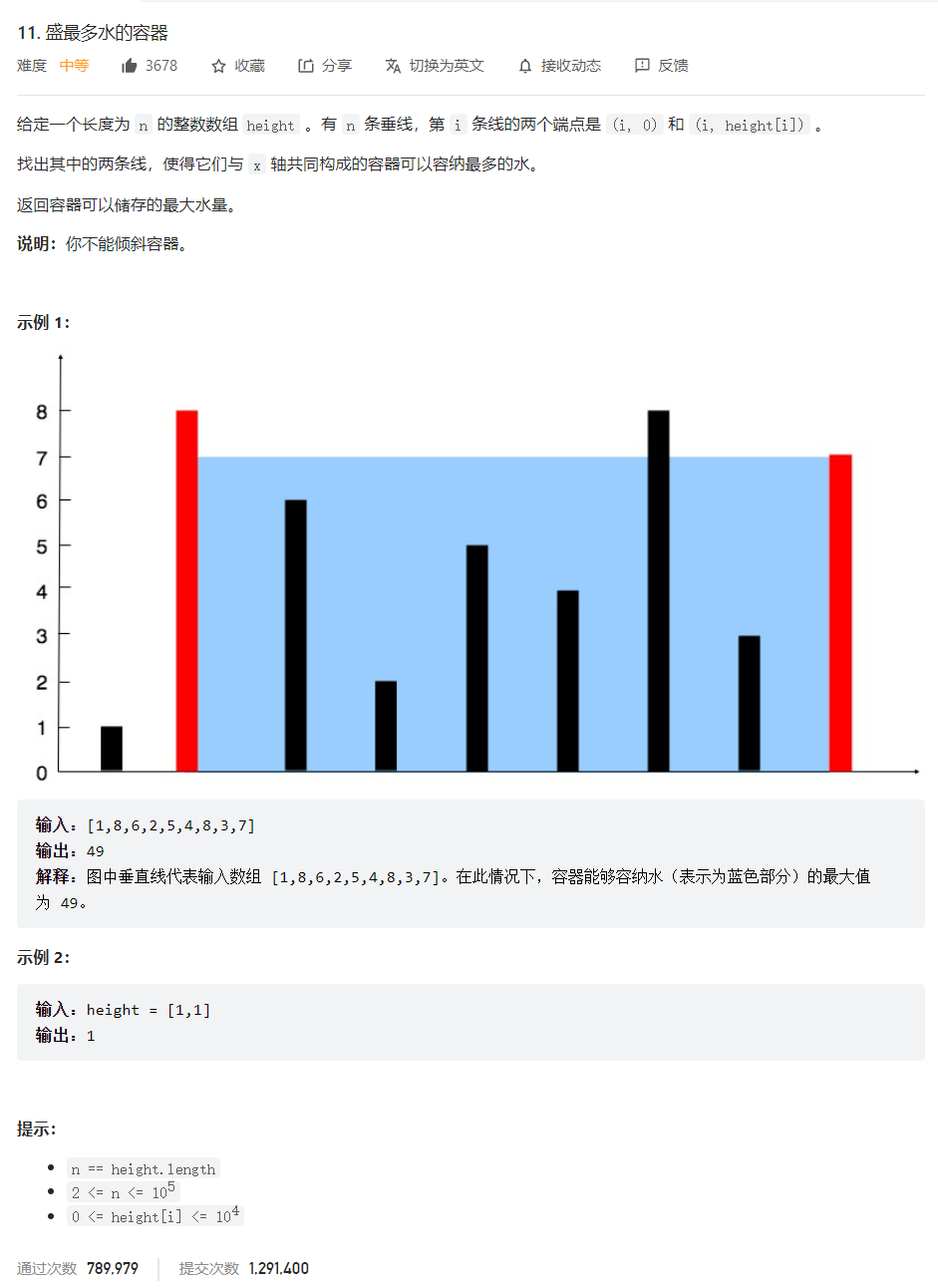
题目描述如下

要找到最大容量
首先确定公式
area=（右左标点-左坐标点）*min（height[左],height[右]）

首先能想到的当然是简单粗暴的暴力解法

func maxArea(height []int) int {
    max:=0
    for i:=1;i<len(height);i++{
        for j:=0;j<i;j++{
            area:=(i-j)*minNum(height[i],height[j])
            max=maxNum(max,area)
        }
    }
    return max
}
func minNum(a int,b int)int{
    if(a<b){return a}
    return b
}
func maxNum(a int,b int)int{
    if(a>b){return a}
    return b
}

让我们看看提交结果

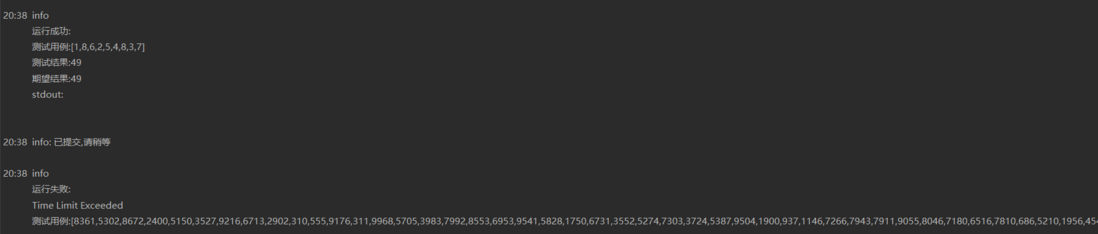
虽然通过了样例，但在提交时由于超出事件限制，不予通过
显然，这道中等难度的题不允许我们用O（n^2）这样辣鸡的算法来解决

要将其优化，我思考过动态规划，分治法，然而显然实现难度都较大
而，双指针，这个神奇的工具，
再一次展示出了他神奇的魅力

上代码

func maxArea(height []int) int {
    max:=0
    left,right:=0,len(height)-1
    for left<right{
        area:=(right-left)*minNum(height[left],height[right])
        max=maxNum(max,area)
        if height[left]<height[right]{
            left++
        }else {
            right--
        }
    }
    return max
}
func minNum(a int,b int)int{
    if(a<b){return a}
    return b
}
func maxNum(a int,b int)int{
    if(a>b){return a}
    return b
}

首先，先将初始状态设置为容器底部最大的状态，同时双指针开始移动，底部逐渐缩小，寻找最大容积

对于边界的移动，每次选择一边木板向内移动，两边的木板按高度分为长板和短板

若向内移动短板 ，水槽的短板 可能变大，因此下个水槽的面积可能增大 。
若向内移动长板 ，水槽的短板 不变或变小，因此下个水槽的面积 一定变小 。

因此，数字较小的这一边不可能再成为边界，可以直接将其排除

每次移动边界一次，便将问题的规模缩小了1，这样直到两个指针重合，我们就把所有的情况考虑了一遍，全局变量max便是最终的结果

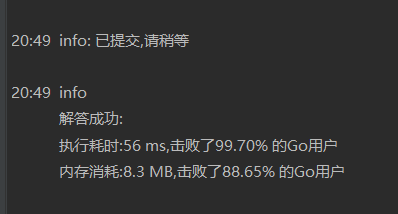
这里只移动了指针n次，算法的复杂度降到了O（n），通过提交便是轻而易举