动态规划的几个前提条件:
最优子结构性质
无后向性
子问题的重叠性
显然这道题是满足动态规划的解题条件的
每个路径的长度取决于之前路径的值
求解最大路径的过程中需要多次用到之前求出的子路径的长度
易得状态转移方程为
当 i>0 且 j>0 时,
当i或j有一个等于0时,则无需考虑子路径的选择,即为
代码
func minPathSum(grid [][]int) int {
//构建一个二维数组
m,n:=len(grid),len(grid[0])
order:=make([][]int,m)
for i:=range order{
order[i]=make([]int,n)
}
//计算路径长度
order[0][0]=grid[0][0]
for i:=1;i<n;i++{
order[0][i]=order[0][i-1]+grid[0][i]
}
for i:=1;i<m;i++{
order[i][0]=order[i-1][0]+grid[i][0]
}
for i:=1;i<m;i++{
for j:=1;j<n;j++{
order[i][j]=grid[i][j]+min(order[i-1][j],order[i][j-1])
}
}
return order[m-1][n-1]
}
func min(a int,b int)int{
if a<b {return a}
return b
}
效果
此时
时间复杂度:O(mn),其中 m 和 n 分别是网格的行数和列数。需要对整个网格遍历一次,计算 dp 的每个元素的值。
空间复杂度:O(mn),其中 m 和 n 分别是网格的行数和列数。创建一个二维数组 dp,和网格大小相同。
空间复杂度可以优化,例如每次只存储上一行的 \textit{dp}dp 值,则可以将空间复杂度优化到 O(n)O(n)
代码
func minPathSum(grid [][]int) int {
//构建一个二维数组
m,n:=len(grid),len(grid[0])
last:=make([]int,n)
now:=make([]int,n)
last[0]=grid[0][0]
for i:=1;i<n;i++{
last[i]=last[i-1]+grid[0][i]
}
now=last
for i:=1;i<m;i++{
now[0]=last[0]+grid[i][0]
for j:=1;j<n;j++{
now[j]=grid[i][j]+min(last[j],now[j-1])
}
last=now
}
return now[n-1]
}
func min(a int,b int)int{
if a<b {return a}
return b
}效果

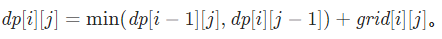



**粗体** _斜体_ [链接](http://example.com) `代码` - 列表 > 引用。你还可以使用@来通知其他用户。