Introduction
This method is mentioned in the Fielded Play: Introduction , and I checked the information to understand it.
Related concepts
limit
Sometimes it is not possible to calculate a value directly, but you can look at the situation as it gets closer, see the following example:
When x = 1 , the result is found to be 0/0 , which is indeterminate in mathematics. Then look at the close situation:
| x | f(x) |
|---|---|
| 0.5 | 1.5 |
| 0.9 | 1.9 |
| 0.99 | 1.99 |
| 0.9999 | 1.9999 |
| 0.999999 | 1.999999 |
It is found that when x is close to 1, f(x) is getting closer and closer to 2, which is the limit .
We can say that when x approaches 1, the limit of f(x) is 2, which is expressed in symbols:
See here for a more formal definition.
Derivative
Let the function f(x) be defined at x 0 if the following limit exists:
Then f(x) is said to be derivable at x 0 , and the above limit is the derivative of f(x) at x 0 , denoted as f ' (x 0 ) .
Derivatives describe the rate of change of a function, and in geometry the slope of the tangent to a point can be calculated through derivatives.
See the derivation rule here .
differential
Let the function y=f(x) be continuous at x 0 , if there is a real number A such that:
Where △x -> 0 , then f(x) is said to be differentiable at x 0 , and the linear part A△x is the differential of f(x) at x 0 , denoted as dy .
The geometric meaning of differential is linear substitution, and the idea of linear substitution can be extended to higher-order substitution.
See here for a more detailed introduction.
Differential equations
Differential equations are equations that contain functions and their derivatives. Some differential equations have infinitely many solutions, some have no solutions, and some have only finite solutions.
The order of a differential equation depends on the order of the highest derivative occurring in the equation.
- Ordinary Differential Equation: A differential equation with only one independent variable.
- Partial Differential Equation: A function that contains two or more independent variables.
- Particular solution: A solution that satisfies a differential equation.
- General solution: A set of solutions that satisfy a differential equation.
- Initial value problem: The solution of an ordinary differential equation that satisfies the initial value condition.
- Single-step method: Computing the value y n+1 of the next point only needs to use the value yn of the previous point.
- Multi-step method: The value y m of the previous m points is needed to calculate the value y n+1 of the next point.
See here and here for more information.
Runge-Kutta
The Runge-Kutta method is a one-step algorithm for solving numerical solutions of ordinary differential equations. One of them is widely used in engineering, called RK4.
For the initial value problem of a first-order differential equation:
where t 0 is the initial time (a known constant), y 0 is the initial state (a known vector), and f(t,y) is a function of time t and state y (a known function).
The RK4 solution algorithm is:
in:
h is the time step.






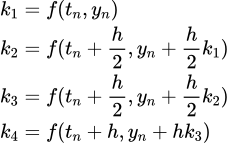
**粗体** _斜体_ [链接](http://example.com) `代码` - 列表 > 引用。你还可以使用@来通知其他用户。