OT扩展协议
首先假设Alice是发送方,Bob是接收方,Bob的𝑚比特长的选择比特串为𝑟,\( 𝑟_𝑗 \)表示选择比特串𝑟的第𝑗比特。Bob产生两个𝑚 × 𝑘的随机矩阵A和B:
用\( 𝑎^𝑖,𝑏^𝑖 \)分别表示矩阵𝐴和𝐵的第𝑖列向量,用\( 𝑎_𝑗,𝑏_𝑗 \)分别表示矩阵𝐴和𝐵的第𝑗行向量。矩阵𝐴和𝐵满足\( 𝑎_𝑗⊕𝑏_𝑗=𝑟_𝑗.1^k \),即若\( 𝑟_𝑗= 1 \),则\( 𝑎_𝑗⊕𝑏_𝑗=1^k \);若\( 𝑟_𝑗=0 \),则\( 𝑎_𝑗 ⊕𝑏_𝑗=0^k \),其中\( 1^k \)表示𝑘比特长的1组成的比特串,\( 0^k \)表示𝑘比特长的0组成的比特串。
发送方Alice随机产生一个𝑘比特长的串𝑠。Alice和Bob之间利用2选1不经意传输协议,根据比特串𝑠的各个比特\( 𝑠_1,…,𝑠_𝑘 \)的值,Bob向Alice发送不同的值。若\( 𝑠_𝑖=0 \),则Bob发送\( 𝑎^𝑖 \);若\( 𝑠_𝑖=1 \),则Bob发送\( 𝑏^𝑖 \)。
当Bob发送完后,Alice获得了一个𝑚×𝑘的矩阵,记为𝐶,
记\( 𝑐^𝑖 \)表示矩阵𝐶的第𝑖列向量,\( 𝑐_𝑗 \)表示矩阵𝐶的第𝑗列向量。那么有结论:\( 𝑐_𝑗=𝑎_𝑗\oplus[𝑟_𝑗.𝑠] \),即若\( 𝑟_𝑗=0 \),则\( 𝑐_𝑗=𝑎_𝑗\oplus[𝑟_𝑗.𝑠]=𝑎_𝑗 \);若\( 𝑟_𝑗=1 \),则\( 𝑐_𝑗=𝑎_𝑗\oplus[𝑟_𝑗.𝑠]=𝑎_𝑗\oplus𝑠 \)。
假设有一个哈希函数𝐻,则Bob可以计算\( 𝐻(𝑐_𝑗) \)和\( 𝐻(𝑐_𝑗\oplus𝑠) \),对于每一个\( 𝑐_𝑗 \),都等于\( 𝑎_𝑗 \)或者\( 𝑎_𝑗\oplus𝑠 \)。Alice 分别使用\( 𝐻(𝑐_𝑗) \)和\( 𝐻(𝑐_𝑗\oplus𝑠) \)来加密秘密\( 𝑥_0 \)和\( 𝑥_1 \),得到\( 𝑒_0=𝐻(𝑐_𝑗)\oplus𝑥_0,𝑒_1= 𝐻(𝑐_𝑗\oplus𝑠)\oplus𝑥_1 \)。
加密之后Alice将\( 𝑒_0 \)和\( 𝑒_1 \)发送给Bob。由于\( 𝑐_𝑗 \)的值为\( 𝑎_𝑗 \)或\( 𝑎_𝑗\oplus𝑠 \),而\( 𝑐_𝑗\oplus𝑠 \)的值为\( 𝑎_𝑗\oplus𝑠 \)或\( 𝑎_𝑗 \),根据\( 𝑟_𝑗 \)的值而定,若\( 𝑐_𝑗 \)为\( 𝑎_𝑗 \)则\( 𝑐_𝑗\oplus𝑠 \)为\( 𝑎_𝑗\oplus𝑠 \);若\( 𝑐_𝑗 \)为\( 𝑎_𝑗\oplus𝑠 \)则\( 𝑐_𝑗\oplus𝑠 \)为\( 𝑎_𝑗 \),二者中必有一个是\( 𝑎_𝑗 \)。
Bob只掌握\( 𝑟_𝑗 \)而不知道\( 𝑠_𝑗 \),Bob又掌握着\( 𝑎_𝑗 \),因此对于Alice发送过来的\( 𝐻(𝑐_𝑗)\oplus𝑥_0 \)和\( 𝐻(𝑐_𝑗\oplus𝑠)\oplus𝑥_1 \),Bob可以本地计算\( 𝐻(𝑎_𝑗) \)来解密\( 𝐻(𝑐_𝑗)\oplus𝑥_0 \)或者\( 𝐻(𝑐_𝑗\oplus𝑠)\oplus𝑥_1 \)中的一个,具体解密哪个取决于\( 𝑟_𝑗 \)的值。矩阵C的每一列都可用来进行一次OT协议,因此可进行𝑘次𝑚比特的OT协议。
假设Bob的选择比特串为𝑟=101,Bob产生两个3×3的随机矩阵A和B,且矩阵A和矩阵B符合\( 𝑎_𝑗\oplus𝑏_𝑗=𝑟_𝑗.1^k \):
可以看到,\( 𝑎_1\oplus𝑏_1= 1.1^k =[1 1 1]^T,𝑎_2\oplus𝑏_2=0.1^k=[0 0 0]^T,𝑎_3\oplus𝑏_3= 1.1^k =[1 1 1]^T \)。
结合具体例子来看:发送方Alice随机产生一个𝑘=3比特长的选择比特串𝑠=[0 0 1],Alice和Bob间利用二选一的不经意传输协议,如之前介绍过的Naor-Pinkas协议,接收根据比特串𝑠的各个比特\( 𝑠_1,𝑠_2,𝑠_3 \)的值,Bob向 Alice发送矩阵A和B的不同列。若\( 𝑠_𝑖=0 \),则Bob发送\( 𝑎^𝑖 \);若\( 𝑠_𝑖=1 \),则Bob发送\( 𝑏^𝑖 \) 。则Alice将收到\( 𝑎^1={[1 0 0]}^T, 𝑎^2={[1 0 0]}^T,𝑏^3={[1 1 1]}^T \)。
将最后Alice收到的矩阵记为𝐶:
可以看到矩阵𝐶满足\( 𝑐_𝑗=𝑎_𝑗\oplus[𝑟_𝑗.𝑠] \),如\( 𝑐_1=𝑎_1\oplus[𝑟_𝑗.𝑠]=𝑎_1\oplus[1.𝑠]= [1 1 0]\oplus[0 0 1]=[1 1 1],𝑐_2= 𝑎_2\oplus[𝑟_2.𝑠]=𝑎_2\oplus[0.𝑠]=𝑎_2=[0 0 1],𝑐_3=𝑎_3\oplus[𝑟_3.𝑠]=𝑎_3 \oplus 𝑠 = [0 1 0]\oplus [0 0 1]=[0 1 1] \)。可以看到矩阵𝐶的各行都满足关系式\( 𝑐_𝑗=𝑎_𝑗 \oplus [𝑟_𝑗.𝑠] \)。
Alice使用矩阵哈希函数H和矩阵C对秘密进行加密,Alice使用\( 𝐻(𝑐_1) \)来加密Alice的秘密\( 𝑥_0 \),使用\( 𝐻(𝑐_1 \oplus 𝑠) \)来加密秘密\( 𝑥_1 \),得到加密后的密文\( 𝑒_0=𝐻(𝑐_1) \oplus 𝑥_0,𝑒_1=𝐻(𝑐_1 \oplus 𝑠) \oplus 𝑥_1 \),之后Alice将\( 𝑒_0 \)和\( 𝑒_1 \)发送给Bob。
注意此时\( 𝐻(𝑐_1)= 𝐻([1 1 1])=𝐻(𝑎_1 \oplus 𝑠),𝐻(𝑐_1 \oplus 𝑠) = 𝐻(𝑎_1 \oplus 𝑠 \oplus 𝑠)=𝐻(𝑎_1) \),Bob是不知道𝑠的,Bob只知道\( 𝑎_1 \) ,当\( 𝑟_1=1 \)时,由于\( 𝐻(𝑐_1 \oplus 𝑠)=𝐻(𝑎_1) \),Bob又掌握\( 𝑎_1 \),因此Bob可以直接计算𝐻(𝑎),由此通过计算\( 𝐻(𝑐_1 \oplus 𝑠) \oplus 𝑥_1 \oplus 𝐻(𝑎_1)=𝑥_1 \),可以解密出\( 𝑥_1 \)。而Bob不知道𝑠,因此Bob无法计算\( 𝐻(𝑎_1 \oplus 𝑠) \),也就无法计算出\( 𝑥_2 \)。
Alice接着又使用\( 𝐻(𝑐_2) \)来加密秘密\( 𝑥_0′ \),使用\( 𝐻(𝑐_2 \oplus 𝑠) \)来加密秘密\( 𝑥_1′ \),得到加密后的密文\( 𝑒_2=𝐻(𝑐_2) \oplus 𝑥_0′, 𝑒_3= 𝐻(𝑐_2 \oplus 𝑠) \oplus 𝑥_1′ \),之后Alice将\( 𝑒_2 \)和\( 𝑒_3 \)发送给Bob。
因为\( 𝑟_2=0 \),因此\( 𝐻(𝑐_2)=𝐻([0 0 1])=𝐻(𝑎_2 \oplus 𝑠) \)
\( 𝐻(𝑐_2 \oplus 𝑠)=𝐻(𝑎_2 \oplus 𝑠 \oplus 𝑠)=𝐻(𝑎_2) \),Bob又掌握\( 𝑎_2 \),因此 Bob可以直接计算\( 𝐻(𝑎_2) \),由此通过计算\( 𝐻(𝑐_2) \oplus 𝑥_0′ \oplus 𝐻(𝑎_2)=𝑥_0′ \),可以解密出\( 𝑥_0 \)。而Bob不知道𝑠,因此 Bob无法计算\( 𝐻(𝑎_2 \oplus 𝑠) \),也就无法计算出\( 𝑥_2 \)。Bob能解密哪个取决于Bob的选择比特串𝑟的各比特值,正如上面的例子,\( 𝑟_0=1 \)时Bob可解密\( 𝑥_1 \);\( 𝑟_1=0 \)时Bob可解密\( 𝑥_0′ \),由此实现不经意传输。
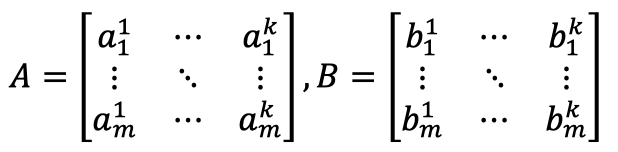

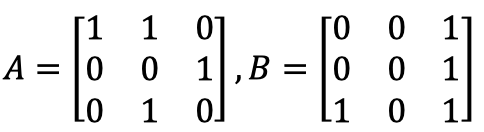





**粗体** _斜体_ [链接](http://example.com) `代码` - 列表 > 引用。你还可以使用@来通知其他用户。