《Lua-in-ConTeXt》02：ConTeXt 计算机

上一篇：Hello world

倘若计算机里有个 ConTeXt 可以用，就可以认为它也是一台计算机，是计算机里的计算机。

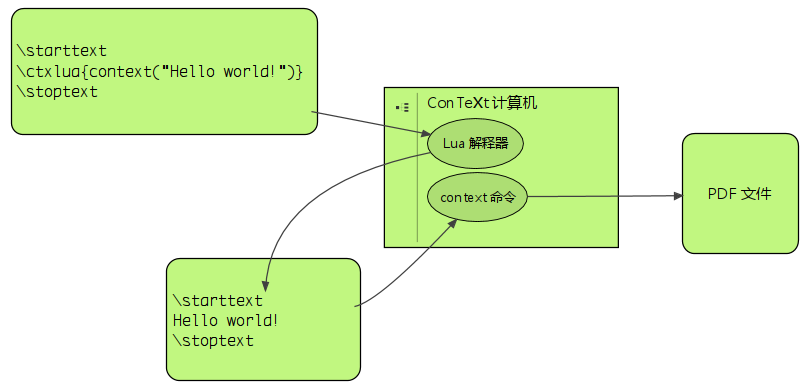
用于编写 TeX 源文件（例如 hello.tex）的任何一种文本编辑器，都可视为「ConTeXt 计算机」的终端。context 命令可将 TeX 源文件里的内容输出到 PDF 文件，于是可将 PDF 文件视为 ConTeXt 计算机的显示器。

单有输入和输出的机器，还称不上计算机，但是倘若在输入里能够编程，那这个机器就肯定是计算机。我们可以在 TeX 源文件里编程，所用的编程语言最早是 TeX 语言。我以前写过一篇没打算写完的文章「TeX 编程」（见本文附录），其中的任何示例代码皆能基于以下格式的 TeX 源文件由 context 命令解释并执行

\starttext
这里可以放任何示例代码
\stoptext

需要说明的是，含有 \starttext ... \stoptext 的 TeX 源文件应当称为 ConTeXt 源文件。TeX 和 ConTeXt 的关系，类似于马和马车的关系。直接骑马也是可以的，但是坐马车会舒服很多。TeX 是 ConTeXt 的内核。像 ConTeXt 这样的马车还有一个，叫 LaTeX，也许听说过它的人要比听说过 ConTeXt 的人更多。

21 世纪了，现代人可以在 TeX 文档里用 Lua 语言编程。Lua 语言本身并不依赖 ConTeXt，使用它可以为我们所熟悉的由一堆硬件组成的计算机编写程序。当 ConTeXt 的开发者将 Lua 语言解释器/编译器嵌入到了 ConTeXt 计算机之后，使用 Lua 语言编写程序时，可以使用 ConTeXt 计算机里大量的资源，这意味着 Lua 语言得到了显著强化。

例如，倘若使用 Lua 编写一个可以生成 PDF 文件的 Hello world 程序，在硬件架构的计算机里，这样的程序可能需要成百甚至上千行代码，而在 ConTeXt 计算机里，只需要三行代码，例如：

\starttext
\ctxlua{context("Hello world!")}
\stoptext

这个程序与上一章里的

\starttext
Hello world!
\stoptext

等价，但是前者出现了真正的 Lua 代码

context("Hello world!")

这行代码调用了 ConTeXt 计算机里的 Lua 函数 context（注意，它不是 context 命令，二者仅仅是恰好同名而已），该函数将字符串 "Hello world!" 输出到了 TeX 文件，然后 ConTeXt 计算机将 ConTeXt 源文件的内容输出至 PDF 文件。

也许通过以下图示，能够理解上述的一切：

现在，可以忘记 ConTeXt 是计算机了，它只是一个程序。我们与它的任何交互，就是通过一条非常简单的 context 命令：

$ context 你的 ConTeXt 源文件

不过，在一个使用着硬件体系的计算机用户看来，Hardware the parts of a computer that can be kicked.（硬件，计算机中可剔除的部分。）

---

附录：TeX 编程

此文大概写于 2018 年 11 月 8 日。我已经忘记了当初为什么没有写下去。以后可能也不会再写下去。不过，有一个好消息，我偶尔发现有人和我有同样的想法，他写了一份比下文更完善的 TeX 编程笔记。

TeX 是一种面向文档排版的计算机编程语言，适用于处理科技文献的排版任务，但本文几乎不关心 TeX 的排版功能，仅从一门完备的编程语言应当具备的要素的角度去认识它。

常量

最基本的常量是单个字符，TeX 解释器会照实对其予以解释。例如

Hello world!

TeX 解释器逐字照实输出。输出到何处？现代的 TeX 解释器，诸如 pdftex、xetex、luatex 等，会将其输出至 PDF 格式的文档。

常量之间只有一种运算，即连接。我们在输入文本时，便已经实施了该运算——将一组字符连成文本。若将一组字符合成为一个常量，可以用 {...}，例如

{Hello world!}

变量

变量可通过无参数的宏予以构造，例如通过 \def 构造一个变量并赋值：

\def\myvar{Hello world!}

\myvar 便是一个变量，它的值为 Hello world!。在 TeX 中，变量只有一种类型，即文本类型。

函数

函数即有参数的宏。我知道它应该叫作宏，但是不要改正我，在这篇文章里我喜欢叫它函数。

函数与变量并没有本质上的区别。所以，在数学中，变量也会被称为常函数。

函数可以吸收常量或变量，将它们与其他常量或变量进行组合。例如，

\def\myfunc#1{#1 world!}

若 \myfunc 吸收了常量 Hello，

\myfunc{Hello}

之后，就会将 Hello 与 world! 连接为 Hello world!。{...} 可将一组字符常量合并为一个常量。在上例中，若不用 {...}，而是直接

\myfunc Hello

结果得到的是「H world!ello」，因此 \myfunc 此时只吸收常量 H，剩下的 ello 只能等待与 \myfunc 的结果连接。

若将 Hello 作为值赋予一个变量，\myfunc 也能吸收这个变量：

\def\hello{Hello}
\myfunc\hello

由于函数与变量并没有本质区别，所以函数也能吸收函数，例如：

\def\foobar#1{#1 {Hello}}
\foobar\myfunc

结果为「Hello world!」。

若一个函数将吸收到的量与这个函数自身进行组合，结果会导致 TeX 解释器陷入到不停地解释这个函数的过程，直至崩溃。例如

\def\foobar#1{#1\foobar{#1}}
\foobar{Hello world!}

在现实世界，类似这种形式的机器叫永动机。与 TeX 世界一样，现实世界也造不出永动机。换言之，若现实世界能造出永动机，那么在 TeX 世界一定也能。

若 \foobar 不吸收任何量，也不与任何量组合，即

\def\foobar{\foobar}
\foobar

在 TeX 的世界里，它可以永动，然而它却什么都不能做了。像 \foobar 这样的宏，在 TeX 中称为递归宏……不是说好了吗不叫宏的吗？递归函数。

寄存器和条件

永动机虽然造不出来，让一个函数自身与其所吸收的量进行组合，这种形式可以产生循环形式的动力。在现实世界，利用这种动力所取得的上天入地效果，我们都有所见识。在 TeX 世界里也能如此，否则就不会有 LaTeX 和 ConTeXt 的出现。但是，要利用这种动力，就需要通过一些开关对其进行控制，否则这种动力便会摧毁整个 TeX 世界。

最简单的开关是控制循环的次数，即控制一个函数自身与其所吸收的量进行组合的次数。这需要使用 TeX 的计数器。使用 \newcount 可以向 TeX 申请一个计数寄存器作为计数器，例如

\newcount\mycount

若让这个计数器从 0 开始，只需

\mycount=0

若要控制函数自身与其所吸收的量进行组合的次数不大于 10 次，只需在该过程中增加控制语句

\ifnum\mycount=10
\else 函数自身与其所吸收的量的组合\advance\mycount by 1
\fi

例如

\def\foobar#1{
  \ifnum\number\mycount=10
  \else #1\advance\mycount by 1\foobar{#1}
  \fi
}

\newcount\mycount
\mycount=0
\foobar{Hello world!}

可将 Hello world! 分段输出十次。

\newcount 的作用是分配一个未使用的计数寄存器，并赋予它一个名字。通过这个名字便可以使用这个计数寄存器中存储的数值。Knuth 的 TeX 最多支持 256 个计数寄存器，现代的 TeX 对此进行了扩展，例如 LuaTeX 可支持 65536 个。可直接以数字为后缀的 \count 使用计数寄存器，例如

\def\foobar#1{
  \ifnum\number\count65534=10
  \else #1\par\advance\count65535 by 1\foobar{#1}
  \fi
}

\count65535=0
\foobar{Hello world!}

但是这样做，很容易引起混乱。例如，倘若某种 TeX 格式将 \count65535 用于存储某个重要的排版数据，这里使用了这个寄存器，那么这个寄存器中原有的值就会被覆盖，可能会导致排版结果出现难以预测的结果。因此，通常推荐使用 \newcount 申请一个尚未被使用的寄存器。这里需要纠正一下前文中的一个说法——TeX 的变量的类型仅有文本类型。事实上，通过 \newcount 构造的计数寄存器本质上是整数类型的变量。

\advance 用于整型变量的加减运算，例如对一个整型变量加 10,再减 30，再增加 1 倍：

\newcount\abc
\abc=0
\advance\abc by 10
\advance\abc by -30
\advance\abc by\abc
\the\abc

结果为 -40。\the 用于攫取整型变量的值。

事实上，TeX 变量的类型还有更多。除了计数寄存器，还有盒子（box）寄存器、维度（dimen）寄存器、skip 寄存器、musikip 寄存器以及 toks 寄存器，这些变量的值皆能用 \the 获取。

\ifnum 用于比较两个数值的关系，即大于、小于和等于。类似的条件语句还有

• \iftrue 永远为真，\iffalse 永远为假；
• \if：测试两个字符是否相同；
• \ifx：测试两个记号（Token）是否相同；
• \ifcat：测试两个记号的类别码是否相同；
• \ifdim：比较两个尺寸的关系；
• \ifodd：测试一个数值是否为奇数；
• ……更多的，见《The TeXbook》第 20 章 ……

这些条件语句，待需要使用它们之时再作细究。

尾递归

利用递归函数可以制作通用的循环语句，例如若制作类似于 TeX 的 \loop ...\repeat 的结构，只需

\def\myloop#1\repeat{\def\body{#1}\myiterate}
\def\myiterate{\body\myiterate\else\relax\fi}

\relax 是个什么都不做的控制序列，将其删除，对 \myloop 毫无影响，但是使用它可以让 \myiterate 的定义更清晰。

现在，用 \myloop ...\repeat 结构将 Hello world! 输出 10 次：

\newcount\mycount
\mycount=0
\myloop Hello world!\advance\mycount by 1\ifnum\mycount<9\repeat

现在来看 \myiterate 的定义……

未完……

另附

在 TeX 编程中，类别码（Category Code）和记号（Token）是非常基础的两个概念。可通过 TeX 的作者 Donald Knuth 所写的《The TeXbook》的第 7 章了解它们。

TeX 按行读取文档中的字符。在该过程中，TeX 会对读入的字符进行分类。在 TeX 看来，字符可分为 16 类，类的编号从 0 到 15。经 TeX 分类后的每个字符构成记号。此外，TeX 的控制序列也构成记号。因此，TeX 读取文档的过程便是生成记号序列的过程，记号序列由字符记号和控制序列记号构成。

字符记号所属的类别决定了 TeX 在读入文档如何理解它们。例如，当 TeX 读入字符 { 时，会将它归为类 1，属于这一类别的字符记号，TeX 会将其视为一个编组的开始符号。当 TeX 读入字符 } 时，会将它归为类 2，属于这一类别的字符记号，TeX 会将其视为一个编组的结束符号。因此，当 TeX 读入类似 {天地一指也，万物一马也。} 这样的字符序列之后，会将 天地一指也，万物一马也。 视为一个编组。

对于一个字符，TeX 本身并不知道它应当归于哪个类别。字符所属类别需要由 TeX 的使用者通过控制序列 \catcode 予以设定，这个控制序列是 TeX 的原始控制序列。不过，在使用某种 TeX 格式排版时，该格式会对字符进行归类，用户只需承认这些归类的合理性，然而心安理得地使用这种 TeX 格式完成排版任务。

TeX 的使用者有时也需要临时地修改某些字符的类别。例如，现在有许多网站支持 TeX 数学公式，但是对于行内公式，这些网站往往会将公式文本放入 \( 和 \) 之间，而不是放入 TeX 所沿袭的一对 $ 之间。若让 TeX 也支持这种形式，只需将 ( 和 ) 的类别编码修改为 11（字母类别），然后便可以定义 \( 和 \) 宏`，之后再复原它们的类别编码：

\catcode`(=11
\catcode`)=11
\def\({$}
\def\){$}
\catcode`(=12
\catcode`)=12

之后，在 TeX 文档里便可以像下面这样写数学公式：

行内公式：\(E=mc^2\)

在 Markdown 中，\( 和 \) 需要写成 \\( 和 \\)。不过，在几乎所有的 TeX 格式中，\ 用作控制序列的开始记号，这样就很难定义 \\(。对于这种情况，不妨先以 \( 和 \) 代替 $，在此基础上，利用文本编辑器的替换功能将 \( 和 \) 替换为 \\( 和 \\)。例如

$ sed -i 's/\\(/\\\\(/g; s/\\)/\\\\)/g' foo.tex

若将文档中的 \\( 和 \\) 再复原为 \( 和 \)，只需

$ sed -i 's/\\\\(/\\\(/g; s/\\\\)/\\\)/g' foo.tex

下一篇：两个世界