编者按
本文系东北大学李俊虎所著,也是「 OceanBase 学术加油站」系列第九篇内容。
「李俊虎:东北大学计算机科学与工程学院在读硕士生,课题方向为数据库查询优化,致力于应用 AI 技术改进传统基数估计器,令数据库选择最优查询计划。」
今天分享的主题是 《HIST,面向海量数据的学习型多维直方图》,从学习型索引方法的 RMI 模型借鉴了结构设计,并在此之上提出了学习型多维直方图,即 LHIST (Learned Histogram) 模型,用于基数估计的学习型数据概要方法。希望阅读完本文,你可以对这个话题有新的收获,有不同看法也欢迎在底部留言探讨。
*原文"LHist : Towards Learning Multi-dimensional Histogram for Massive Spatial Data",发表于 ICDE 2021,可点击文末“阅读全文”下载全篇论文查看。
多维直方图 (Multi-dimensional histogram, MH) 技术被广泛用于查询的基数估计,空间数据分片,空间数据挖掘等方向。然而,目前的 MH 方法存在以下缺陷:
- 不合理的假设: 为了减少空间代价,MH 和其它的数据摘要方法一样需要随机采样过程,这极度依赖 dimension-wise independence 或者 intra-bucket uniform distribution 两个理想化的假设。
- 不稳定的性能: 目前已有的 MH 方法的估计效果很容易受不同数据集的影响,参数设置,查询负载等。已经有研究证明了 MH 的高准确率需要更高的存储代价。
受最近提出的学习型索引模型的启发,比如 RMI 模型 [1]通过集成简单的机器学习模型改进广泛使用的 B-tree 索引结构。本文从学习型索引方法的 RMI 模型借鉴了结构设计,并在此之上提出了能解决上述两种缺陷的学习型多维直方图,即 LHIST (Learned Histogram) 模型,它是一个完全由数据驱动的,可用于基数估计的学习型数据概要方法。LHIST 模型的设计有两方面:
第一,可描述复杂多维直方图的累计密度函数 CDF。
第二,能很好地平衡内存和准确率两项指标。
实验证明 LHIST 在存储成本,查询处理效率和精度方面都要优于传统的数据概要方法。
问题定义
数据点 Point:一个向量 x = (x(1), x(2),..., x(d)) 是一个欧几里得空间,其中 x(i)表示向量 x 的第 i 维元素。
超矩形 Hyper-rectangle:一个超矩形可被符号化定义,如下
公式 1 超矩形定义
超矩形解析自查询语句,每个数组表示了谓词的覆盖区间,比如 age > 18 AND age < 24 可以被解析为 [18, 24]。使用 X 表示空间数据集,则 X ∩ R 表示某个查询所覆盖到的数据空间,| X ∩ R | 则表示该查询的 COUNT 结果 (或者称之基数)。
学习型空间概要 Learned Spatial Synopsis:定义一个函数 f ,它接受 R 作为输入,并输出 |X ∩ R|。
学习型索引RMI
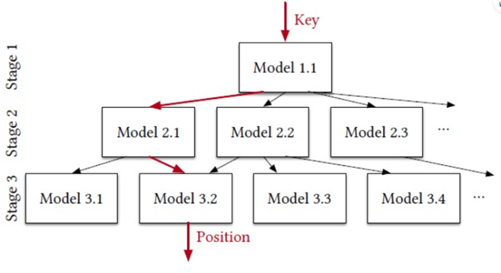
本文的模型结构借鉴于[1]提出的 RMI ( Recursive Model Index ),它是一个学习型索引模型,用于挖掘键值 key 以及排序索引位置 idx(key) 的关系。RMI 是一个层次结构 (而非树形结构),当输入 key 值时,模型会依据自身结构自上而下地进行搜索,并在叶子节点返回预测的索引位置 idx(key)。
更具体来讲,每一层 stage 的模型会预测 key 值的索引位置范围,并据此决定继续传递给下一层 stage 的哪个模型。越靠近底层的模型越能给出更加精确的预测,缩小搜索范围。显然,RMI 模型本身由多个小型的模型组成,相比于单个的大型模型,这些小型模型的组合更易于训练,节省空间和算力。
图 1 RMI 模型的层次结构
简而言之,RMI 的核心思想是将整个 key 空间分解成更小的空间,这样索引位置分布的累计密度函数 CDF 就更容易使用多个小型的线性模型去拟合。根据[1]的实验表明,相比于 B-tree 结构,该架构的学习型索引能够将存储代价降低 99%。
RMI 可以用作一维数据概要,因为它本质上表示主键分布函数 CDF,这类似于一维直方图等其他统计概要结构。然而,要将这个想法扩展到多维数据具有挑战性,因为与一维数据不同,多维数据点之间没有明确的排序顺序。
有一种解决方案是借助空间填充曲线,将 k 维空间数据映射成 1 维,随后使用降维的数据训练 RMI 模型。诸如 z-order 曲线或者是 Hilbert 曲线都是可行的降维方案,但问题在于,在数据降维的过程中存在信息丢失,因此基于这种方案的拓展 RMI 方法会损失部分估计的精确度。
另一种方案则是直接用模型学习空间数据的联合分布函数,最近提出的 Naru [2]和 DeepSPACE [3]就是典型的,通过自回归模型拟合多维数据联合分布的例子。这些研究均宣称它们的模型显著改善了基数估计的准确性,然而这些模型仍然不能很好地实现准确率与存储空间的平衡。
本文则基于 RMI 的架构之上提出了对 MEH 的改进方案。
LUIST结构
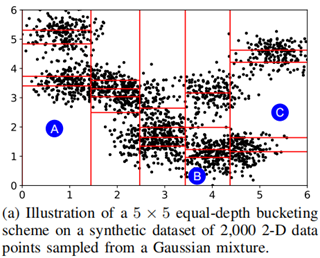
图 2 MEH 对 2D 数据的切分演示
首先以二维 (d = 2) 多维等深直方图 MEH 为例子,设 bucket = 5。首先在 "纵向" 按照等深策略分割空间数据 X,即 5 个数据域内的样本点数量保持相同;其次,按照同样的策略对每个数据域再进行 "横向" 切割,并最终得到 5 × 5 = 25 个等深区域。
本文提出的 LHIST 模型可以被概括为学习型 MEH。即,相较于上述的等深 "硬分割" 策略,本文使用简单的线性模型对每一维度的数据边界进行 "软分割",每个数据区域称之为桶 bucket。
图 3 LHSIT 结构展示
LHIST 则仿照 RMI 的层次结构构建了一个完全 k 叉树回归模型,如图 3 所示,其中 k 为每一个数据维度的划分数量。设数据点 x 是一个 d 维向量,则回归模型将沿着自上而下的 stage 依次对这 d 维数据列进行分割。
LHIST 在前 d - 1 的 stage 将整个 d 维数据集分解成小桶,然后在最后一层 stage 训练模型来近似桶内分布 CDF。与之前简单地将直方图与拟合曲线相结合的研究不同 [4],本文 LHIST 模型的桶分区策略和桶内分布 CDF 估计都是由简单机器学习模型实现得到,它们很容易被优化。为此,LHIST 可以生成一个完全数据驱动的分桶方案,同时避免不切实际的假设,最终构建出一个高效,低存储的多维直方图。
LHIST 的结构能以递归的形式进行定义。在 LHIST 的第一个 stage 定义根节点 R,它代表了整个数据集。fR 表示了回归模型,它接受输入向量 x,并首先输出 x 在第 1 个维度的索引位置 idx(1)(x) ,即:
公式 2 根节点在第 1 维对数据划分
在 LHIST 中,可以使用任何一个以非递减作为约束条件的回归模型。在训练 fR 之后,整个数据集 X 将被划分成 k 个桶。从 R 节点划分出的第 i 个桶可以符号化表示为:
公式 3 节点的数据分片记作 Buckets
每个桶 Bj(R) 将沿着第 2 个维度继续搜寻索引位置 idx(2)(x),即:
公式 4 基于 Buckets 在第 2 维继续对数据划分
推广到更一般的情形,对于第 i 个层级 ( i = 2,..., d - 1 ) 的任意一个节点 A,令 XA 表示 A 节点覆盖的数据空间,记 NA = |XA|。
在构建 LHIST 之后,模型将在前 d - 1 个 stage 中把整个数据空间 X 分成 k d-1个桶,每个桶最终都将关联一个叶子节点。最后第 d 层的叶子节点将负责构造第 d 维数据的桶内分布。
对于给定分为查询所对应的超矩形 R,其基数估计可以符号化表示为:
公式 5 将基数估计问题转换为节点求和问题
其中,超矩形 R 所覆盖的叶子节点 A 构成了一个集合。对于被覆盖的每个节点 A,模型通过 x(d) 谓词的范围计算出当前节点的基数估计结果。比如,给定一个谓词 [20, 40],基数 = |fA(40) - fA(20)|。而又由于每个叶子节点之间是相互独立的,因此将所有被覆盖节点的结果做加和即可求得某范围查询 R 对应的 COUNT 基数。
与 RMI 相比,LHIST 是一个严谨的树形结构,而 RMI 结构中的一个子节点可以存在多个父节点,这会导致 RMI 模型需要更多的空间来存储参数,维持层次结构。
函数选择
前文曾提及 fA 可以是任意一个非递减的回归模型。但实际上,模型的选择对 LHIST 的精度和存储运算产生深刻的影响。
作为最简单的模型,线性回归模型 (比如 f(x) = ax + b) 非常容易存储和训练。然而,仅使用线性函数很难描述现实数据中复杂的 CDF。另一方面,虽然模型的层次越深,就越能描述复杂的 CDF,但是这会导致参数调优变得异常困难,这样的模型不符合 LHIST 的性能要求。
作为性能和存储的最佳权衡,本文选取了单变量多项式函数,它能够灵活地控制模型的复杂度,即 ploy(x) = w0 + w1·x + ... + wp · xp,p 作为多项式的度数。用户可以通过设置 p 来决定更高的精度,或者是更低的存储空间。
假定 {(xi, yi)}i=1,...n 是一组容量为 n 的样本点,其中 yi∈{ 1, ... , n } 是 xi 对应的索引次序,紧接着,一组 poly(xi) 的拟合函数可以如下表示:
公式 6 权值 W 即模型的优化目标
令 y = [y1, ... , yn]T 是参考值向量,p 是预测值向量。本文的建模问题可以转换为最小二乘问题:
公式 7 将基数估计转换为最小二乘问题
此处设置条件约束 ploy'(x)≥0 的目的是保证 ploy(x) 是非递减函数,这满足 CDF 的语义。进一步,本文通过数学方法将非递减作为约束的最小二乘问题转化成了半正定规划:
公式 8 将公式 7 转换为半正定规划问题
最终,模型通过该规划的约束条件学习 W = [w0, w1, ... wp] T,并使得模型的误差最小。
与MEH方法的比较
和单纯的 MEH 方法相比,LHIST 对存储预算的利用率更高。本质上,每一条 MEH entry 都需要一个整数存储频率,并且使用一个浮点数存储桶的边界。给定同等的存储空间,经过训练的紧凑型回归模型可以在不作任何理想假设的前提下编码更多的局部分布信息。
在相同的存储预算下,本文的 LHIST 在精度方面比 MEH 高出 24 倍,运行效率方面则比 MEH 高出 1.8 倍。
▋实验部分
一、数据集及其参数设置
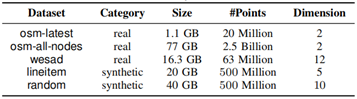
本实验中使用的数据集如下:
表 1 实验用空间数据集
作为对比实验,本实验对以下超参数进行了不同的设置:
表 2 对内存,多项式度,选择率的设置
参与比较的方法有:
表 3 参与对比的多种模型
随机采样法。随机采样法有两种策略,即简单随机采样 (RS) 以及分层采样 (SS)。
多维直方图。和 [5]类似,本文实现了两种直方图作为对比,即均匀直方图 (UH) 以及多维等深直方图 (MEH)。
RMI。如前文所述,当前的方法结合了 z-order 方法实现了 1-D RMI 线性回归模型,以构建数据概要。
深度无监督学习。这里使用了具有代表性的 Naru 模型,本文按照由小到大的次序创建了三个不同规模的模型实例:Naru-s (small),Naru-m (middle),Naru-l (large)。
LHIST。本文实现了三种 LHIST 结构:LHIST + 线性回归 (l-LHIST),LHIST + 分段线性回归 (plr-LHIST),LHIST + 多项式回归 (p-LHIST)。
为了评估基数估计器的准确度,这里选取公式 9 作为评估标准:
公式 9 模型衡量指标
二、准确度评估
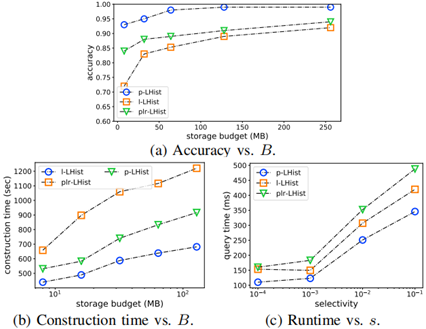
图 4 不同模型在不同选择率下的准确率性能
图 4 绘制了范围查询的基数估计模型在不同内存预算下的准确率表现。通常情况下,给定更多的预算 B 能够提高以上方法的准确率。除了 RMI 方法之外,其它方法在预算足够 (budget = 128 MB) 且查询选择度足够高的情形下 (Selectivity = 10 -1) 能够达到超过 95% 的准确率,这验证了前文的观点:应用 z-order 等降维手段会影响 RMI 模型估计的准确率。
与 Naru 相比,LHIST 能够在选择度 >10 -3的情况下达到相近的性能。然而 LHIST 在低选择度查询的表现则更加稳定。在低选择度下,增加 Naru 的神经元数量反而会降低准确率,因为 DL 模型学习联合分布的过程是不可解释的;而 LHIST 则可以用很小的内存预算保留多维数据的完整信息。
三、构建代价
传统数据概要方法的构建代价显然要更小,因此这里重点观察并对比学习型的方法:Naru,RMI,以及 LHIST。结果对比见图 5:
图 5 不同模型基于不同数据集的构建代价
在学习型数据概要方法中,LHIST 的构建时间总体最短,仅比非学习型的 MEH 方法稍微耗时一些。值得注意的是,Naru 总是需要最多的模型构建时间。尤其是在最大的数据集 osm-all-nodes 上,Naru-m 需要将近 8 小时的时间进行训练,这主要是受到了 GPU 内存限制的影响。
四、推理时延
图 6 不同模型在不同内存预算下的推理时延
图 6 展示了 osm-all-nodes 数据集上,不同模型对范围 COUNT 查询的处理时延。本文使用了前缀和技巧优化了均匀直方图 UH,因此在当前的实验中,它只需要常数量级的代价。
RMI 的处理效率接近于常量,因为它只需要计算R 的下边界 R.xH 和上边界 R.xL;Naru 的处理效率接近于常量,这主要取决于模型的复杂度。
本文通过实验观察到,LIHIST 模型要比 MEH 的效率高出 1.1 ~ 1.9 倍。这是因为 MEH 的桶分区是非均匀的,因此该方法需要多轮二分查找才可以定位到某个区域,尤其是分桶变得十分复杂时,MEH 的查找将消耗显著的时间。相比之下,LHIST 只需要经过固定的 d 层 stage,且每一层模型都是简单的多项式。
五、不同子模型的选择
本文比较了 LHIST 下的几个不同子模型,并且在 wesad 数据集上做了实验,实验结果如图 7。
图 7 不同函数选择对推理效率的影响
总体来说,使用多项式作为 fA 能够在效率和准确率当中达到一个最佳的平衡。与 l-LHIST 方法相比,p-LHIST 只需要更少的桶数量,因此它可以更快地遍历 HLIST 树。不仅如此,p-LHIST 可以在非常有限的内存预算中达到更高的准确率。
六、多项式度 p 的影响
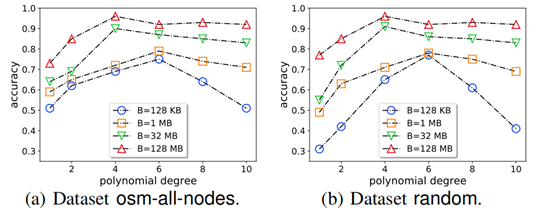
为了测试不同 p 对 p-LHIST 性能的影响,本文分别在 osm-all-nodes 和 random 两个数据集下做了两个实验,这里将测试查询的选择度固定为 10 -3。
图 8 p 值对准确率的影响呈单峰函数
可以观察到图像接近单峰函数,当 p ∈ [4, 6] 时,模型的准确率接近达到最高值。除此之外,研究还表明,当模型需要处理高维数据时,选取最佳的度数 p 将变得至关重要。这是因为维度 d 越大,则数据空间越稀疏。此时需要更加细粒度的数据划分,从而保证桶内的数据分布 CDF 更加容易学习。
相关工作
本文首先讨论并比较已有的数据概要以及学习型索引。
- 直方图。 多维直方图可以联合数据分布的近似。STHoles [6]是一种查询驱动的直方图方法,根据查询负载来对数据进行分区。本文的方法则是完全数据驱动的方法,并将未来的负载感知优化作为未来的工作。
- 学习型索引。 已有的研究已证明了 B-tree 的索引结构可以被简单的机器学习模型所替代,比如 RMI [1]。目前还有很多学者开始了对学习型索引的研究。比如 Ding 等人提出了名为 ALEX [7]的,可适应动态负载的学习型 B-tree。
如本文所述,想要将 1-D 学习型索引拓展到多维数据库是一个具有挑战的任务,因为数据点通常没有明确的排序关系。
- AI in DB。 除了学习型索引之外,机器学习还广泛地应用到了连接代价估计, [8], [9],查询优化器 [10], [11],和 DBMS 自调参 [12], [13]。
本文的工作可被归类为学习型基数估计以及近似查询处理,如 DeepSPACE 和 Naru 模型。然而,目前的学习型估计器的通用性较差,主要是无法实现存储和精度之间的权衡。
写在最后
本文提出的 LHIST 属于空间数据概要框架,它可被看作是 MEH 的学习型版本。LHIST 完全由数据驱动,并且不依赖专家经验调整模型参数。经过实验表明,LHIST 在效率和准确率方面均优于传统的数据摘要方法。
*参考文献:
[1] T. Kraska, A. Beutel, E. H. Chi, J. Dean, and N. Polyzotis, “The case for learned index structures,” in SIGMOD Conference. ACM, 2018, pp. 489–504.
[2] Z. Yang, E. Liang, A. Kamsetty, C. Wu, Y. Duan, P. Chen, P. Abbeel, J. M. Hellerstein, S. Krishnan, and I. Stoica, “Deep unsupervised cardinality estimation,” PVLDB, vol. 13, no. 3, pp. 279–292, 2019.
[3] D. Vorona, A. Kipf, T. Neumann, and A. Kemper, “DeepSPACE: Approximate geospatial query processing with deep learning,” in SIGSPATIAL/GIS. ACM, 2019, pp. 500–503.
[4] A. C. König and G. Weikum, “Combining histograms and parametric curve fitting for feedback-driven query result-size estimation,” in VLDB. Morgan Kaufmann, 1999, pp. 423–434.
[5] A. B. Siddique, A. Eldawy, and V. Hristidis, “Comparing synopsis techniques for approximate spatial data analysis,” Proc. VLDB Endow., vol. 12, no. 11, pp. 1583–1596, 2019.
[6] N. Bruno, S. Chaudhuri, and L. Gravano, “STHoles: A multidimensional workload-aware histogram,” in SIGMOD Conference. ACM, 2001, pp. 211–222.
[7] J. Ding, U. F. Minhas, J. Yu, C. Wang, J. Do, Y. Li, H. Zhang, B. Chandramouli, J. Gehrke, D. Kossmann, D. B. Lomet, and T. Kraska, “ALEX: an updatable adaptive learned index,” in SIGMOD Conference. ACM, 2020, pp. 969–984.
[8] J. Sun and G. Li, “An end-to-end learning-based cost estimator,” PVLDB, vol. 13, no. 3, pp. 307–319, 2019.
[9] B. Hilprecht, A. Schmidt, M. Kulessa, A. Molina, K. Kersting, and C. Binnig, “DeepDB: Learn from data, not from queries!” Proc. VLDB Endow., vol. 13, no. 7, pp. 992–1005, 2020.
[10] R. C. Marcus, P. Negi, H. Mao, C. Zhang, M. Alizadeh, T. Kraska, O. Papaemmanouil, and N. Tatbul, “Neo: A learned query optimizer,” PVLDB, vol. 12, no. 11, pp. 1705–1718, 2019.
[11] C. Wu, A. Jindal, S. Amizadeh, H. Patel, W. Le, S. Qiao, and S. Rao, “Towards a learning optimizer for shared clouds,” PVLDB, vol. 12, no. 3, pp. 210–222, 2018.
[12] T. Kraska, M. Alizadeh, A. Beutel, E. H. Chi, A. Kristo, G. Leclerc, S. Madden, H. Mao, and V. Nathan, “SageDB: A learned database system,” in CIDR. www.cidrdb.org, 2019.
[13] S. Idreos, N. Dayan, W. Qin, M. Akmanalp, S. Hilgard, A. Ross, J. Lennon, V. Jain, H. Gupta, D. Li, and Z. Zhu, “Design continuums and the path toward self-designing key-value stores that know and learn,” in CIDR. www.cidrdb.org, 2019.



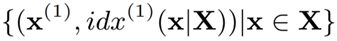
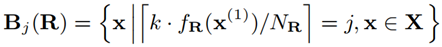
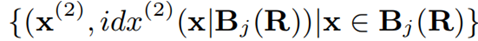
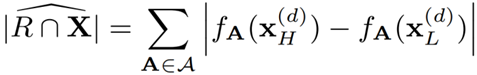
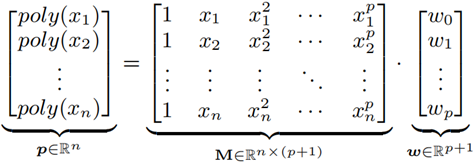
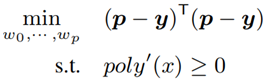
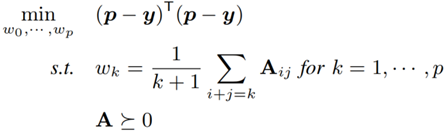


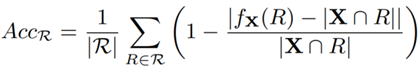



**粗体** _斜体_ [链接](http://example.com) `代码` - 列表 > 引用。你还可以使用@来通知其他用户。