三方复制秘密共享(二)
上次科普介绍了在布尔电路下的三方复制秘密共享方案,这次科普介绍把它扩展到环 \( 2^n \) 下的方式。
首先是在环\( 2^n \)下生成三个随机数 \( 𝑎_1,𝑎_2,𝑎_3 \) ,并且满足 \( 𝑎_1+𝑎_2+𝑎_3=0 \) 。上次科普已经介绍过满足条件 \( 𝑎_1⊕𝑎_2⊕𝑎_3=0 \) 的随机数生成方式,满足条件满足 \( 𝑎_1+𝑎_2+𝑎_3=0 \) 的只需对上次的方式进行一些小更改:
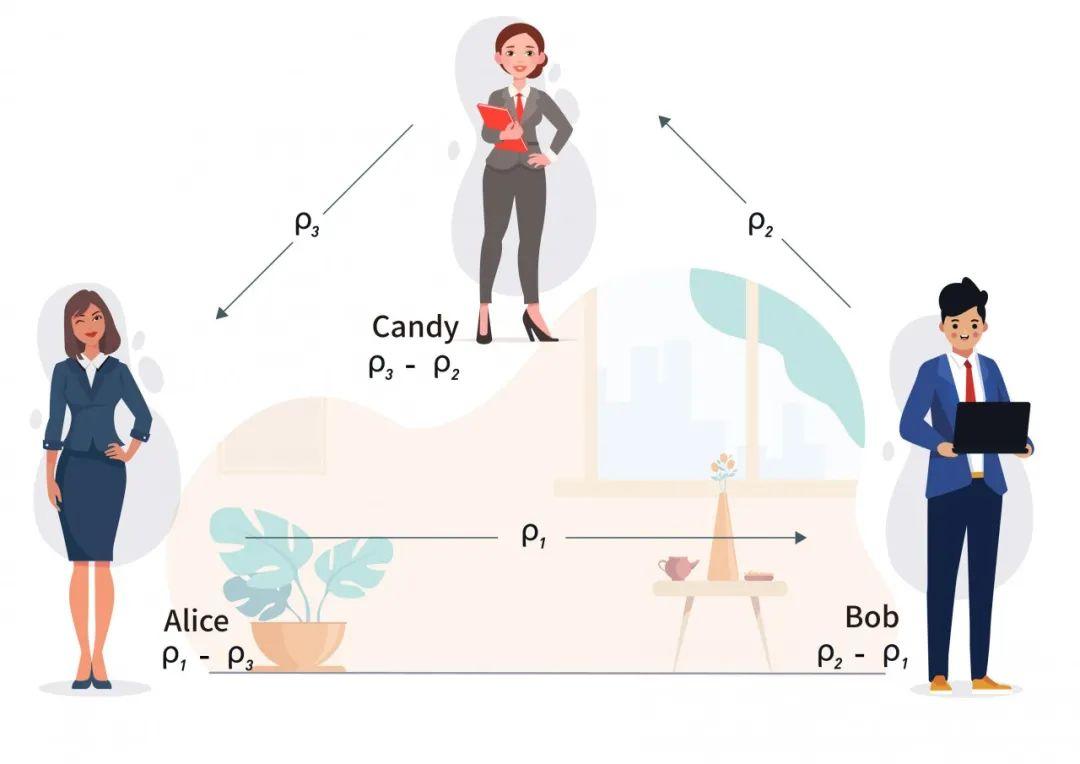
Alice、Bob、Candy分别生成随机数𝜌1,𝜌2,𝜌3,Alice将𝜌1发送给Bob,Bob将𝜌2发送给Candy,Candy将𝜌3发送给Alice。接着Alice计算𝑎1=𝜌1−𝜌3,Bob计算𝑎2=𝜌2−𝜌1,Candy计算𝑎3=𝜌3−𝜌2。
显然,\( 𝑎_1+𝑎_2+𝑎_3 \)= 𝜌1−𝜌3+𝜌2−𝜌1+𝜌3−𝜌2=0。
--三方产生满足𝑎1+𝑎2+𝑎3=0的随机数--
假设秘密为𝑥, 𝑦,则\( 𝑥_1=𝑎_3−𝑥,𝑥_2=𝑎_1−𝑥,𝑥_3=𝑎_2−𝑥;𝑦_1=𝑏_3−𝑦,𝑦_2=𝑏_1−𝑦,𝑦_3=𝑏_2−𝑦 \)。Alice持有\( (𝑥_1,𝑎_1), (𝑦_1,𝑏_1) \),Bob持有\( (𝑥_2,𝑎_2), (𝑦_2,𝑏_2) \),Candy持有\( (𝑥_3, 𝑎_3), (𝑦_3, 𝑏_3) \)。
加法的实现方式为:布尔电路上的加法原理相同,Alice、Bob和Candy在模下直接本地计算\( 𝑥_𝑖+𝑦_𝑖 \)即可。如Alice计算
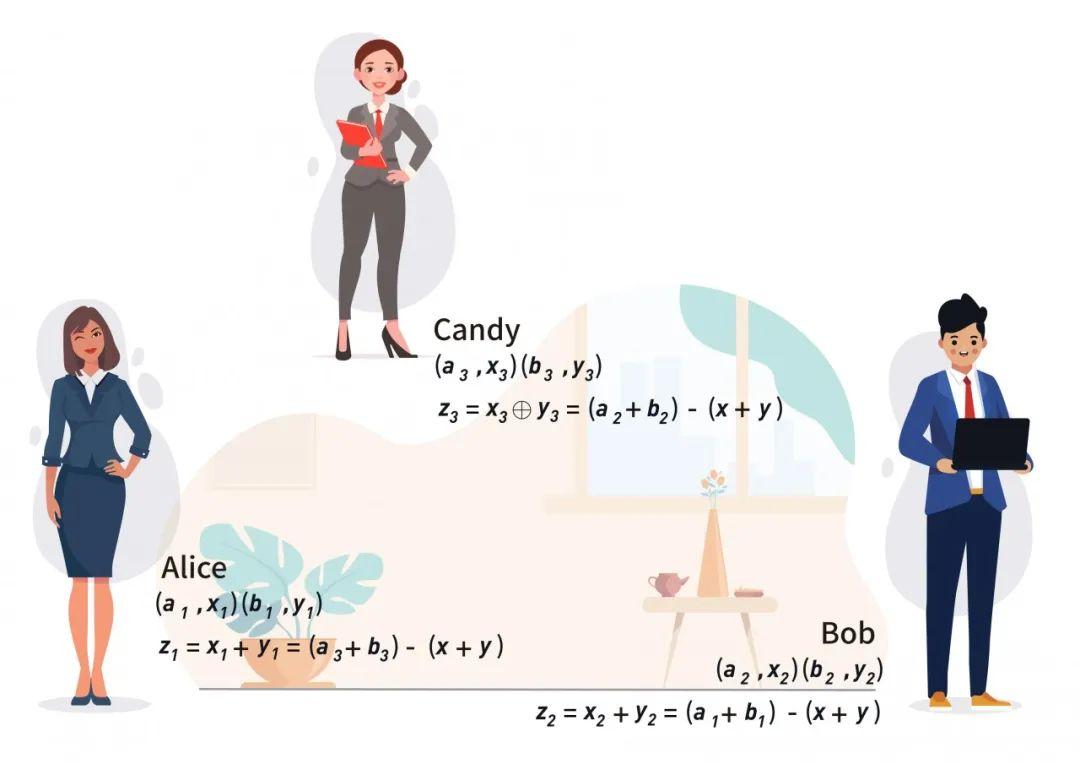
\( 𝑧_1=𝑥_1+𝑦_1=𝑎_3−𝑥+𝑏_3−𝑦=(𝑎_3+𝑏_3)−(𝑥+𝑦),𝑐_1=𝑎_1+𝑏_1 \)。同理Bob计算\( 𝑧_2=𝑥_2+𝑦_2=𝑎_1−𝑥+𝑏_1−𝑦=(𝑎_1+𝑏_1)−(𝑥+𝑦),𝑐_2=𝑎_2+𝑏_2 \);Candy计算
\( 𝑧_3=(𝑥_3+𝑦_3)=𝑎_2−𝑥+𝑏_2−𝑦=(𝑎_2+𝑏_2)−(𝑥+𝑦),𝑐_3=𝑎_3+𝑏_3 \)。可以验证:
--三方加法实现方式--
乘法的实现方式为:
Alice、Bob和Candy利用上述的随机数生成方式,生成满足𝛼+𝛽+𝛾=0,条件随机数𝛼, 𝛽, 𝛾。Alice计算\( r_{1}=\frac{x_{1} y_{1}-a_{1} b_{1}+\alpha}{3} \),并且把𝑟1发送给Bob;Bob计算\( r_{2}=\frac{x_{2} y_{2}-a_{2} b_{2}+\beta}{3} \),并且把𝑟2发送给Candy;Candy计算\( r_{3}=\frac{x_{3} y_{3}-a_{3} b_{3}+\gamma}{3} \),并且把𝑟3发送给Alice。
Alice让\( 𝑧_1=−2𝑟_3−𝑟_1,𝑐1=𝑟_3−𝑟_1 \);
Bob让\( 𝑧_2=−2𝑟_1−𝑟_2,𝑐2=𝑟_1−𝑟_2 \);
Candy让\( 𝑧_3=−2𝑟_2−𝑟_3,𝑐_3=𝑟_2−𝑟_3 \)。
显然:\( 𝑐_1+𝑐_2+𝑐_3=𝑟_3−𝑟_1+𝑟_1−𝑟_2+𝑟_2−𝑟_3=0 \),可以验证:
因此有:
同理可推导出,\( 𝑧_2=𝑐_1−𝑥𝑦,𝑧_3=𝑐_2−𝑥𝑦 \),正确性得证
--三方乘法实现方式--

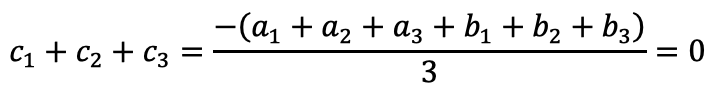

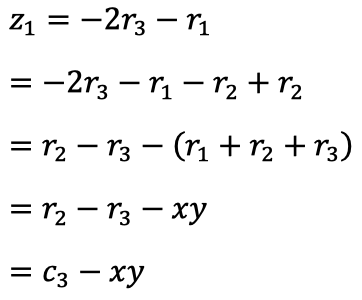

**粗体** _斜体_ [链接](http://example.com) `代码` - 列表 > 引用。你还可以使用@来通知其他用户。