文章和代码已经归档至【Github仓库:algorithms-notes】或者公众号【AIShareLab】回复 算法笔记 也可获取。
树状数组
注意:树状数组的坐标一定要从1开始!
树状数组的应用主要是:快速(在O(logn)的复杂度内):
- 在某个位置上加上一个数(单点修改)
- 求某一个的前缀和(区间查询)
其他的变式都是由这两个基本功能转换而来,例如单点查询,区间修改等等。
它与纯前缀和的区别在于可以单点修改。假如直接用前缀和进行单点修改,则它每次都会更新修改值后面的前缀和,因此会导致每个都更新一遍,复杂度为O(n)了。
简单的比较:
| 单点修改 | 区间查询 | 综合 | |
|---|---|---|---|
| 前缀和 | O(n) | O(1) | (O(n) + O(1)) / 2 = O(n) |
| 线段数组 | O(logn) | O(logn) | O(logn) |
基本思想
其中原数组为A,树状数组为C。每一层的关系如上所示,可以发现,相同个数的后缀0的数在同一层,比如2--->10, 6 ---> 110。
其中:
- C[1] = A[1]
- C[2] = A[2] + C[1] = A[2] + A[1]
- C[3] = A[3]
- C[4] = A[4] + C[3] + C[2] = A[4] + A[3] + A[2] + A[1]
- ...
核心:C[x] = (x - lowbit(x), x]
lowbit = x & -x = $2 ^ k$ 作用是统计二进制数字中后缀0的个数。
模板
在某个位置上加上一个数(单点修改)
// a[x] + v
// x 的父节点是 x + lowbit(x)
for(int i = x; i <= n; i += lowbit(x))
c[x] += v;求某一个的前缀和(区间查询)
int res = 0;
for(int i = x; i > 0; i -= lowbit(i))
res += c[i];
return res核心函数
// lowbit函数
int lowbit(int x)
{
return x & -x;
}void add(int x, int v)
{
// i节点的父节点是 i + lowbit(i),每个父节点都要进行修改
for (int i = x; i <= n; i += lowbit(i)) tr[i] += v;
}int query(int x)
{
int res = 0;
// 递归的方式
for (int i = x; i; i -= lowbit(i)) res += tr[i];
return res;
}模板题:动态求连续区间和
给定 n 个数组成的一个数列,规定有两种操作,一是修改某个元素,二是求子数列 [a,b] 的连续和。
输入格式
第一行包含两个整数 n 和 m,分别表示数的个数和操作次数。第二行包含 n 个整数,表示完整数列。
接下来 m 行,每行包含三个整数 k, a, b (k=0,表示求子数列[a,b]的和;k=1,表示第 a 个数加 b)。数列从 1 开始计数。
输出格式
输出若干行数字,表示 k=0 时,对应的子数列 [a,b] 的连续和。
数据范围
$1≤n≤100000$,
$1≤m≤100000$,
$1≤a≤b≤n$,
数据保证在任何时候,数列中所有元素之和均在 int 范围内。
输入样例:
10 5
1 2 3 4 5 6 7 8 9 10
1 1 5
0 1 3
0 4 8
1 7 5
0 4 8输出样例:
11
30
35code:
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 100010;
int n, m;
int a[N], tr[N];
// 核心操作
int lowbit(int x)
{
return x & -x;
}
void add(int x, int v)
{
// i节点的父节点是 i + lowbit(i),每个父节点都要进行修改
for (int i = x; i <= n; i += lowbit(i)) tr[i] += v;
}
int query(int x)
{
int res = 0;
// 递归的方式
for (int i = x; i; i -= lowbit(i)) res += tr[i];
return res;
}
int main()
{
scanf("%d%d", &n, &m);
// 初始化原数组
for (int i = 1; i <= n; i ++ ) scanf("%d", &a[i]);
// 初始化树状数组
for (int i = 1; i <= n; i ++ ) add(i, a[i]);
while (m -- )
{
int k, x, y;
scanf("%d%d%d", &k, &x, &y);
if (k == 0) printf("%d\n", query(y) - query(x - 1));
else add(x, y);
}
return 0;
}数星星
天空中有一些星星,这些星星都在不同的位置,每个星星有个坐标。
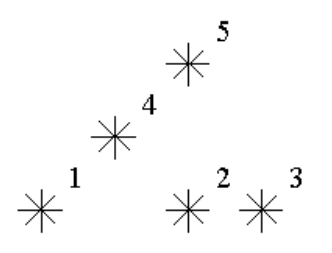
如果一个星星的左下方(包含正左和正下)有 k 颗星星,就说这颗星星是 k 级的。
例如,上图中星星 5 是 3 级的(1,2,4 在它左下),星星 2,4 是 1 级的。
例图中有 1 个 0 级,2 个 1 级,1 个 2 级,1 个 3 级的星星。给定星星的位置,输出各级星星的数目。
换句话说,给定 N 个点,定义每个点的等级是在该点左下方(含正左、正下)的点的数目,试统计每个等级有多少个点。
输入格式
第一行一个整数 N,表示星星的数目;
接下来 N 行给出每颗星星的坐标,坐标用两个整数 x,y 表示;
不会有星星重叠。星星按 y 坐标增序给出,y 坐标相同的按 x 坐标增序给出。
输出格式
N 行,每行一个整数,分别是 0 级,1 级,2 级,……,N−1 级的星星的数目。
数据范围
$1≤N≤15000$,
$0≤x,y≤32000$
输入样例:
5
1 1
5 1
7 1
3 3
5 5输出样例:
1
2
1
1
0code:
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 32010;
int n;
// tr[i]统计x坐标为i的个数
int tr[N], level[N];
int lowbit(int x)
{
return x & -x;
}
void add(int x)
{
for (int i = x; i < N; i += lowbit(i)) tr[i] ++ ;
}
// 查询x≤i的坐标的数,即当前星星的等级
int sum(int x)
{
int res = 0;
for (int i = x; i; i -= lowbit(i)) res += tr[i];
return res;
}
int main()
{
scanf("%d", &n);
for (int i = 0; i < n; i ++ )
{
int x, y;
scanf("%d%d", &x, &y);
// 树状数组的下标必须从1开始,因此需要先执行x ++,把所有坐标同一向右平移1即可
x ++ ;
// 为了避免查到自己,在 add 之前就先查询一下
level[sum(x)] ++ ;
// 然后再添加自己即可
add(x);
}
for (int i = 0; i < n; i ++ ) printf("%d\n", level[i]);
return 0;
}
**粗体** _斜体_ [链接](http://example.com) `代码` - 列表 > 引用。你还可以使用@来通知其他用户。