地图投影

地图投影

为了更好地展示地球上的数据，需要将地球投影到一个平面上。地图投影是一个数学问题，按照一定的几何关系，将地球上的经纬度坐标映射到一个平面上的坐标。地球投影有很多种，每种投影都有自己的优缺点。本文介绍一些常用的地球投影。

什么是地图投影

投影，在数学上的含义是建立两个面之间点与点、线与线的对应关系。同样地，地图投影的定义是：建立地球椭球面(或球体表面)与地图平面之间点与点或线与线的一一对应关系。

地图投影的变形通常有长度变形、面积变形和角度变形。在实际应用中，根据地图的使用目的，通常会限定某种变形。

地球是一个球体，而我们的屏幕是一个平面，所以我们需要将地球投影到一个平面上，这样才能在屏幕上显示地球的数据。

目的

• 方便看图或者展示地理信息；
• 制作平面地图；
• 建立投影坐标系；
• 气象学分析；

种类

把球形的地球投影到平面上，一定会有形变或者扭曲，这种形变有很多种，不同的投影方式会有不同的形变。根据变形性质，常见的地图投影有：

• 等角投影(正形投影)：保持线和线的夹角不变，这是关注的的重点；
• 等面积投影：保持面积不变；
• 等距投影：保持距离不变；
• 等形状投影：保持形状不变；

等角投影保证了角度不变，也就保证了方向不变，使用该投影可以保证地图上的方向是正确的，这种地图投影适合用于航海、飞行等需要方向准确的领域。是我们关注的重点。

等角投影的分类

• 极地投影
• 兰伯特投影
• 墨卡托投影

重点介绍墨卡托投影，因为它是日常开发中遇到最多的投影方式。

墨卡托投影

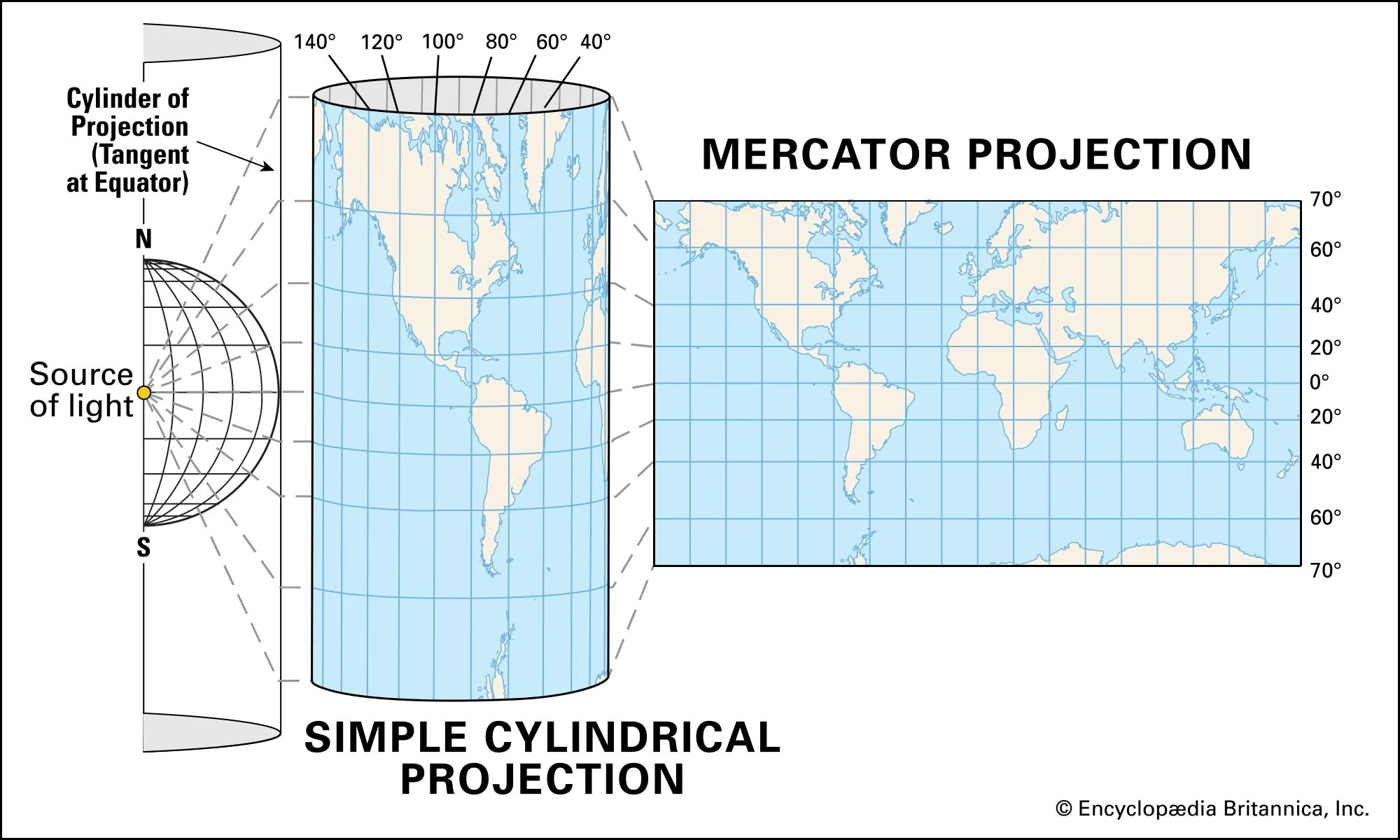
1569年，由比利时数学家墨卡托（Gerardus Mercator）提出的一种地图投影方法，是最常用的地图投影方法之一。墨卡托投影是一种等角圆柱投影，它将地球表面投影到一个圆柱体上，然后再展开到一个平面上。

一个圆柱体套住地球，光线从球心射出。

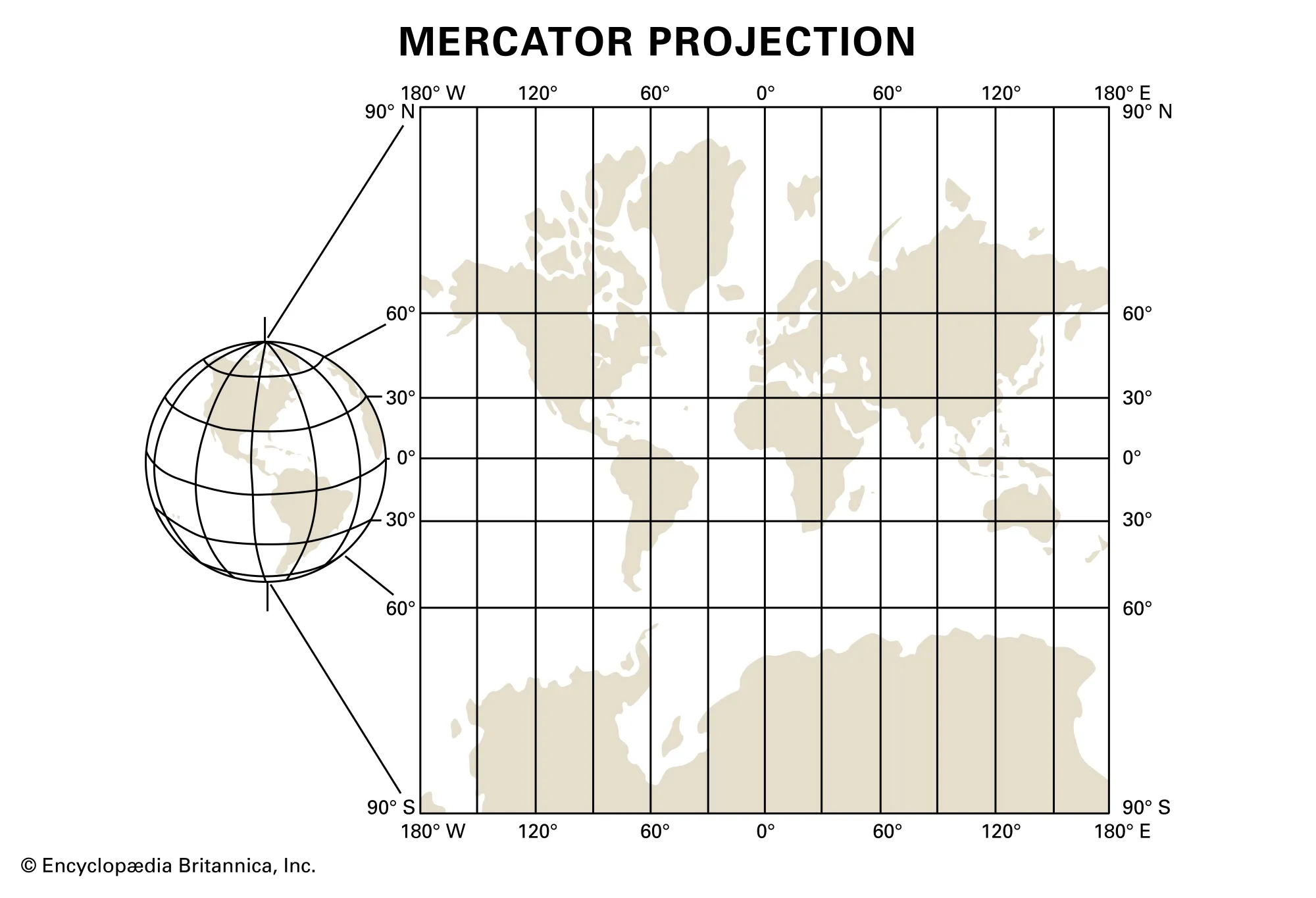
墨卡托投影的特点是保持角度不变，是一种等角投影，地球上两直线的夹角，投影到平面上，角度不变，但是会有面积变形，即在地图的高纬度地区，面积会被放大。由于等角不变的特点，保证了投影后方向和相对位置不变，因此墨卡托投影在航海、飞行等需要方向准确的领域中应用广泛。

Web 墨卡托投影

2005年，Google Maps 推出，使用 Web 墨卡托投影，这种投影方式在 web 地图中得到了广泛应用，已经是 web 地图的事实标准。

EPSG 投影编码为 3857，即 EPSG:3857 。

地球是一个两极扁赤道略长的椭球体，而 Web 墨卡托投影把地球简化成一个正球体，两极半径和赤道半径相等了。

web 墨卡托水平方向(经度方向)没有变形，但是竖直方向(维度方向)随着维度的变大，长度被拉伸了，维度越高，拉伸越大。

经过 web 墨卡托投影以后，以赤道为标准纬线，本初子午线为中央经线，两者的交点为原点，向东、向北为正，向西、向南为负。

赤道半径R = 6378137米, PI = 3.14159265359, 则

X 轴范围：[-20037508.342789244, 20037508.342789244], 而 Y 轴，从投影上看，越靠近极点，会被拉伸到无穷远，google 的工程师干脆就取和 X 一样的范围，因此世界地图是一个正方形。

最小坐标为[-20037508.342789244, -20037508.342789244]，最大坐标 [-20037508.342789244, 20037508.342789244]。

合法的经纬度范围为： [-180, -85.06, 180, 85.06] 。

为何是 85.05 呢？

我计算出来是 71.57 。

计算方法是：

tanX = PI*R/R = PI = 3.14159265359
X = 71.57

后在网上查询资料，发现是 85.06 ，原因是：

y = ln(tan(π/4 + φ/2)) # 当 φ = 85.06 时，tan(π/4 + φ/2) = ∞

不太明白这个公式，但是可以理解，因为墨卡托投影在极点处会无限拉伸，所以不能显示。

参考

陈志强同学-b站课程 - 投影

墨卡托投影是怎么把一个“球”变成一张“图纸”的呢？

Web Mercator 公开的小秘密

投影、坐标与瓦片

小结

• 地图投影是将地球投影到一个平面上，以便展示地球上的数据；
• 地图投影有很多种，每种投影都有自己的优缺点；
• 墨卡托投影是一种等角投影，保持角度不变，适合航海、飞行等需要方向准确的领域；
• Web 墨卡托投影是一种等角投影，保持角度不变，但是会有面积变形，纬度越高变形越严重，适合 web 地图展示。