算数编码原理解析

上一篇讲了LZW编码，本篇讨论另一种不同的编码算法，算数编码。和哈夫曼编码一样，算数编码是熵编码的一种，是基于数据中字符出现的概率，给不同字符以不同的编码。本文也会对这两种编码方式的相似和不同点进行比较。

编码原理

算数编码的原理我个人感觉其实并不太容易用三言两语直观地表达出来，其背后的数学思想则更是深刻。当然在这里我还是尽可能地将它表述，并着重结合例子来详细讲解它的原理。

简单来说，算数编码做了这样一件事情：

1. 假设有一段数据需要编码，统计里面所有的字符和出现的次数。
2. 将区间 [0,1) 连续划分成多个子区间，每个子区间代表一个上述字符， 区间的大小正比于这个字符在文中出现的概率 p。概率越大，则区间越大。所有的子区间加起来正好是 [0,1)。
3. 编码从一个初始区间 [0,1) 开始，设置:$$low = 0，high = 1$$
4. 不断读入原始数据的字符，找到这个字符所在的区间，比如 [ L, H )，更新:

$$low = low + (high - low) * L \\\ high = low + (high - low) * H$$

1. 最后将得到的区间 [low, high)中任意一个小数以二进制形式输出即得到编码的数据。

乍一看这些数学和公式很难给人直观理解，所以我们还是看例子。例如有一段非常简单的原始数据：

ARBER

统计它们出现的次数和概率：

Symbol	Times	P
A	1	0.2
B	1	0.2
E	1	0.2
R	2	0.4

将这几个字符的区间在 [0，1) 上按照概率大小连续一字排开，我们得到一个划分好的 [0，1)区间：

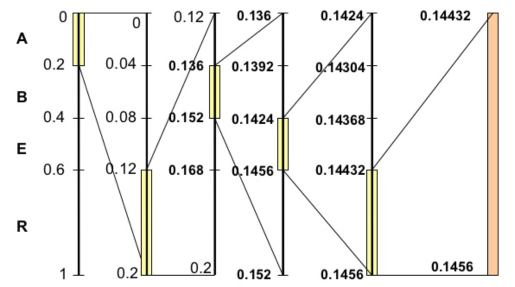
开始编码，初始区间是 [0，1)。注意这里又用了区间这个词，不过这个区间不同于上面代表各个字符的概率区间 [0，1)。这里我们可以称之为编码区间，这个区间是会变化的，确切来说是不断变小。我们将编码过程用下图完整地表示出来：

拆解开来一步一步看：

1. 刚开始编码区间是 [0，1)，即$$low = 0\\\ high = 1$$
2. 第一个字符A的概率区间是 [0，0.2)，则 L = 0，H = 0.2，更新

$$low = low + （high - low）* L=0\\\quad high = low + （high - low）* H=0.2$$

1. 第二个字符R的概率区间是 [0.6，1)，则 L = 0.6，H = 1，更新

$$low = low + （high - low）* L=0.12\\high = low + （high - low）* H=0.2$$

1. 第三个字符B的概率区间是 [0.2，0.4)，则 L = 0.2，H = 0.4，更新

$$low = low + （high - low）* L=0.136\\\ \ high = low + （high - low）* H=0.152$$

1. ......

上面的图已经非常清楚地展现了算数编码的思想，我们可以看到一个不断变化的小数编码区间。每次编码一个字符，就在现有的编码区间上，按照概率比例取出这个字符对应的子区间。例如一开始A落在0到0.2上，因此编码区间缩小为 [0，0.2)，第二个字符是R，则在 [0，0.2)上按比例取出R对应的子区间 [0.12，0.2)，以此类推。每次得到的新的区间都能精确无误地确定当前字符，并且保留了之前所有字符的信息，因为新的编码区间永远是在之前的子区间。最后我们会得到一个长长的小数，这个小数即神奇地包含了所有的原始数据，不得不说这真是一种非常精彩的思想。

解码

如果你理解了编码的原理，则解码的方法显而易见，就是编码过程的逆推。从编码得到的小数开始，不断地寻找小数落在了哪个概率区间，就能将原来的字符一个个地找出来。例如得到的小数是0.14432，则第一个字符显然是A，因为它落在了 [0，0.2)上，接下来再看0.14432落在了 [0，0.2)区间的哪一个相对子区间，发现是 [0.6，1)， 就能找到第二个字符是R，依此类推。在这里就不赘述解码的具体步骤了。

编程实现

算数编码的原理简洁而又精致，理解起来也不很困难，但具体的编程实现其实并不是想象的那么容易，主要是因为小数的问题。虽然我们在讲解原理时非常容易地不断计算，但如果真的用编程实现，例如C++，并且不借助第三方数学库，我们不可能简单地用一个double类型去表示和计算这个小数，因为数据和编码可以任意长，小数也会到达小数点后成千上万位。

怎么办？其实也很容易，小数点是可以挪动的。给定一个编码区间，例如从上面例子里最后的区间 [0.14432，0.1456)开始，假定还有新的数据进来要继续编码。现有区间小数点后的高位0.14其实是确定的，那么实际上14已经可以输出了，小数点可以向后移动两位，区间变成 [0.432，0.56)，在这个区间上继续计算后面的子区间。这样编码区间永远保持在一个有限的精度要求上。

上述是基于十进制的，实际数字是用二进制表示的，当然原理是一样的，用十进制只是为了表述方便。算数编码／解码的编程实现其实还有很多tricky的东西和corner case，我当时写的时候debug了好久，因此我也建议读者自己动手写一遍，相信会有收获。

算数编码 vs 哈夫曼编码

这其实是我想重点探讨的一个部分。在这里默认你已经懂哈夫曼编码，因为这是一种最基本的压缩编码，算法课都会讲。哈夫曼编码和算数编码都属于熵编码，仔细分析它们的原理，这两种编码是十分类似的，但也有微妙的不同之处，这也导致算数编码的压缩率通常比哈夫曼编码略高，这些我们都会加以探讨。

不过我们首先要了解什么是熵编码，熵是借用了物理上的一个概念，简单来说表示的是物质的无序度，混乱度。信息学里的熵表示数据的无序度，熵越高，则包含的信息越多。其实这个概念还是很抽象，举个最简单的例子，假如一段文字全是字母A，则它的熵就是0，因为根本没有任何变化。如果有一半A一半B，则它可以包含的信息就多了，熵也就高。如果有90%的A和10%的B，则熵比刚才的一半A一半B要低，因为大多数字母都是A。

熵编码就是根据数据中不同字符出现的概率，用不同长度的编码来表示不同字符。出现概率越高的字符，则用越短的编码表示；出现概率地的字符，可以用比较长的编码表示。这种思想在哈夫曼编码中其实已经很清晰地体现出来了。那么给定一段数据，用二进制表示，最少需要多少bit才能编码呢？或者说平均每个字符需要几个bit表示？其实这就是信息熵的概念，如果从数学上理论分析，香农天才地给出了如下公式：
$$ H(x) = -\sum_{i=1}^{n}p(x_{i})\log_{2}p(x_{i})$$
其中 p (xi) 表示每个字符出现的概率。log对数计算的是每一个字符需要多少bit表示，对它们进行概率加权求和，可以理解为是求数学期望值，最后的结果即表示最少平均每个字符需要多少bit表示，即信息熵，它给出了编码率的极限。

算数编码和哈夫曼编码的比较

在这里我们不对信息熵和背后的理论做过多分析，只是为了帮助理解算数编码和哈夫曼编码的本质思想。为了比较这两种编码的异同点，我们首先回顾哈夫曼编码，例如给定一段数据，统计里面字符的出现次数，生成哈夫曼树，我们可以得到字符编码集：

Symbol	Times	Encoding
a	3	00
b	3	01
c	2	10
d	1	110
e	2	111

仔细观察编码所表示的小数，从0.0到0.111，其实就是构成了算数编码中的各个概率区间，并且概率越大，所用的bit数越少，区间则反而越大。如果用哈夫曼编码一段数据abcde，则得到：

00 01 10 110 111

如果点上小数点，把它也看成一个小数，其实和算数编码的形式很类似，不断地读入字符，找到它应该落在当前区间的哪一个子区间，整个编码过程形成一个不断收拢变小的区间。

由此我们可以看到这两种编码，或者说熵编码的本质。概率越小的字符，用更多的bit去表示，这反映到概率区间上就是，概率小的字符所对应的区间也小，因此这个区间的上下边际值的差值越小，为了唯一确定当前这个区间，则需要更多的数字去表示它。我们仍以十进制来说明，例如大区间0.2到0.3，我们需要0.2来确定，一位足以表示；但如果是小的区间0.11112到0.11113，则需要0.11112才能确定这个区间，编码时就需要5位才能将这个字符确定。其实编码一个字符需要的bit数就等于 -log ( p )，这里是十进制，所以log应以10为底，在二进制下以2为底，也就是香农公式里的形式。

-------
哈夫曼编码的不同之处就在于，它所划分出来的子区间并不是严格按照概率的大小等比例划分的。例如上面的d和e，概率其实是不同的，但却得到了相同的子区间大小0.125；再例如c，和d，e构成的子树，c应该比d，e的区间之和要小，但实际上它们是一样的都是0.25。我们可以将哈夫曼编码和算术编码在这个例子里的概率区间做个对比：

这说明哈夫曼编码可以看作是对算数编码的一种近似，它并不是完美地呈现原始数据中字符的概率分布。也正是因为这一点微小的偏差，使得哈夫曼编码的压缩率通常比算数编码略低一些。或者说，算数编码能更逼近香农给出的理论熵值。

为了更好地理解这一点，我们举一个最简单的例子，比如有一段数据，A出现的概率是0.8，B出现的概率是0.2，现在要编码数据：

AAA...........AAABBB...BBB  (800个A，200个B)

如果用哈夫曼编码，显然A会被编成0，B会被编成1，如果表示在概率区间上，则A是 [0, 0.5)，B是 [0.5, 1)。为了编码800个A和200个B，哈夫曼会用到800个0，然后跟200个1：

0.000......000111...111  (800个0，200个1)

在编码800个A的过程中，如果我们试图去观察编码区间的变化，它是不断地以0.5进行指数递减，最后形成一个 [0, 0.5^800) 的编码区间，然后开始B的编码。

但是如果是算数编码呢？因为A的概率是0.8，所以算数编码会使用区间 [0, 0.8) 来编码A，800个A则会形成一个区间 [0, 0.8^800)，显然这个区间比 [0, 0.5^800) 大得多，也就是说800个A，哈夫曼编码用了整整800个0，而算数编码只需要不到800个0，更少的bit数就能表示。

当然对B而言，哈夫曼编码的区间大小是0.5，算数编码是0.2，算数编码会用到更多的bit数，但因为B的出现概率比A小得多，总体而言，算术编码”牺牲“B而“照顾”A，最终平均需要的bit数就会比哈夫曼编码少。而哈夫曼编码，由于其算法的特点，只能“不合理”地使用0.5和0.5的概率分布。这样的结果是，出现概率很高的A，和出现概率低的B使用了相同的编码长度1。两者相比，显然算术编码能更好地实现熵编码的思想。

---
从另外一个角度来看，在哈夫曼编码下，整个bit流可以清晰地分割出原始字符串：

而在算数编码下，每一个字符并不是严格地对应整数个bit的，有些字符与字符之间的边界可能是模糊的，或者说是重叠的，所以它的压缩率会略高：

当然这样的解释并不完全严格，如果一定要究其原因，那必须从数学上进行证明，算数编码的区间分割是更接近于信息熵的结果的，这就不在本文的讨论范围了。在这里我只是试图用更直观地方式解释算数编码和哈夫曼编码之间微妙的区别，以及它们同属于熵编码的本质性原理。

总结

算数编码的讲解就到这里。说实话我非常喜欢这种编码以及它所蕴含的思想，那种触及了数学本质的美感。如果说哈夫曼编码只是直观地基于概率，优化了字符编码长度实现压缩，那么算术编码是真正地从信息熵的本质，展现了信息究竟是以怎样的形式进行无损压缩，以及它的极限是什么。在讨论算术编码时，总是要提及哈夫曼编码，并与之进行比较，我们必须认识到它们之间的关系，才能对熵编码有一个完整的理解。