随机森林简易教程

简介

基于树的学习算法被认为是最优秀的，也是使用最广泛的监督型学习方法。基于树的算法赋予预测模型高精度、稳定性和易解释性。与线性模型不同，它们能很好地映射非线性关系。它们善于解决手头上的任何问题，包括分类和回归。

例如Decision Trees，Random Forest，Gradient Boosting等方法，在各种数据科学问题中得到了广泛的应用。因此，对于每一个分析师来说，学会这些算法并使用它们进行建模是很重要的。

目录

1. 什么是决策树，以及它是如何工作的？
2. 回归树Vs分类树
3. 决策树是如何决定分割点的？
4. 模型建立的关键参数是什么？如何避免决策树的过拟合？
5. 基于树的模型优于线性模型吗？
6. 在R和Python中使用决策树。
7. 基于树的模型的集成方法（Ensemble Methods）是什么？
8. 什么是装袋（Bagging）？它是如何工作的？
9. 什么是随机森林？它是如何工作的？
10. 什么是Boosting？它是如何工作的？
11. GBM和Xgboost哪个更强大？
12. 在R和Python中使用GBM。
13. 在R和Python中使用Xgboost。

1. 什么是决策树，以及它是如何工作的？

决策树是在分类问题中经常使用到的一种监督型学习算法。它适用于分类型以及连续性输入和输出变量。在这个方法中，我们根据输入变量中最显著的分裂点将总体或样本划分为两类或多类。

例子：

假如有30个同学，已知他们的性别（Gender：Boy／Girl），班级（Class：IX／X）和身高（Hight：5-6 ft）。其中15个同学在业余时间打板球（cricket）。现在，我想建立一个模型预测谁在业余时间打板球？在这个问题中，我们需要根据高度显著的输入变量来区分在业余时间中打板球的同学。

决策树能够帮助我们，它根据三个变量的所有值划分学生，并识别哪个变量的划分效果最好。在下图中，你可以看到与其它两个变量相比，性别（Gender）的划分效果最好。

如上所述，决策树识别出最显著的变量以及取值，并给出效果最好的划分结果。那么，现在的问题是：它如何识别最显著的变量，以及如何进行分裂？为此，决策树使用了各种算法，我们将在下面的章节中讨论。

决策树类型

决策树的类型取决于我们的目标变量的类型。共分为两类：

1. 分类型变量决策树：目标变量为分类型的决策树，称为分类型变量决策树。例如上面的“学生是否在业余时间打板球”。
2. 连续型变量决策树：目标变量为连续型的决策树，称为连续型变量决策树。

例子：假如我们要预测一个客户是否会向保险公司支付续期保险费（是／否）。在这里，我们知道客户的收入是一个显著性变量，但保险公司没有所有客户的收入情况。可是，我们可以基于客户的职业，所买产品以及其它变量建立一个决策树模型去预测客户的收入。在这个例子中，我们预测的是连续变量的值。

决策树相关重要术语

让我们看看与决策树相关的一些基本术语：

1. 根节点（Root Node）：代表整个总体或样本。
2. 分裂（Splitting）：将一个节点分成两个或多个子节点的过程。
3. 决策节点（Decision Node）：当一个子节点（sub-node）进一步分成子节点时，我们称这个节点为决策节点。
4. 叶子/终端节点（Leaf/Terminal Node）：不再分裂的节点称为叶子或终端节点。

1. 剪枝（Pruning）：我们把移除一个决策节点的子节点的过程称为剪枝。也可以称之为和分裂相反的处理过程。
2. 分支/子树（Branch/Sub-Tree）：整棵树的一个子部分叫做分支或子树。
3. 父节点和子节点（Parent and Child Node）：被分裂为sub-nodes的节点称为sub-nodes的父节点，而这些sub-nodes称为这个节点的子节点。

这些是决策树常用的术语。我们知道每种算法都有优缺点，下面是我们应该了解的关于决策树的一些优缺点：

优点

1. 易于理解：决策树的输出易于理解，即使是没有分析背景的人也很容易解释。它不需要任何统计知识来阅读和解释它们。它的图形表示非常直观，用户可以很容易地将它们的假设联系起来。
2. 在数据探索过程中很有用：决策树是识别最显著变量以及两个或多个变量之间关系的最快速的方法之一。在决策树的帮助下，我们可以创建新的变量/特征，以便能够更好地预测目标变量。它也可以在数据探索阶段发挥作用。例如：现在我们有100个变量的信息，决策树可以帮助我们识别出最显著的变量。
3. 需要少量的数据清洗工作：与其它模型相比，决策树只需要少量的数据清洗工作。它不受离群值和缺失值对公平度的影响。
4. 数据类型没有限制：它可以处理数值型以及分类型变量。
5. 无参方法：决策树是一种无参方法。这意味着决策树对空间分布以及分类器结构没有任何假设。

缺点

1. 过拟合：过拟合是决策树模型中最为困难的问题之一。可以通过设置模型参数和修剪来解决这个问题。
2. 不适合连续性变量：处理连续数值型变量问题上，当决策树将变量划分为不同类别时，将会导致信息的丢失。

2.回归树Vs分类树

我们知道终端节点（叶子节点）位于决策树的最底部。这意味着决策树是一棵颠倒的树，叶子在下面，根在上面，如下图所示：

这两种树的工作原理几乎相同，让我们看看分类和回归树之间的主要区别和相似之处：

1. 当因变量为连续型变量时，使用回归树；当因变量为分类型变量时，使用分类树。
2. 在回归树中，训练数据中叶子节点得到的值是该区域内观测值的平均响应值。因此，如果一个数据观测值落在那个区域（叶子节点），我们将用这个区域内所有观测值的平均值作为它的预测值。
3. 在分类树中，训练数据中叶子节点得到的值（类别）是该区域内的观测模式。因此，如果一个数据观测落在那个区域，我们将用这个区域内的模型作为它的预测类别。
4. 这两种树将预测空间（自变量）分成不同的和不重叠的区域。为了简单起见，可以将这些区域视为高维空间中的一个个不重叠的空间。
5. 两种树都遵循一种自上而下的称为递归二进制分裂的贪婪方法。之所以称之为“自上而下”是因为：它从树顶开始，并不断地将预测空间分割为两个新的分支。之所以称之为“贪婪”是因为：该算法每次都寻找最佳分割变量，只考虑当前的最优分裂，并不关心如何在整体上得到一个最好的分裂。
6. 分裂过程一直持续进行，直到用户定义停止条件为止。例如：当节点的观察数小于50时，我们可以告诉算法停止分裂。
7. 这两种情况下，持续地分裂将会导致完全成熟的树，直到达到停止条件。但是，完全长大的树极有可能导致过拟合，使得模型的泛化能力较弱。这就产生了“剪枝”的概念。剪枝是一种解决过拟合的技术。我们将在下面的章节中进一步了解它。

3.决策树是如何决定分割点的？

分割的方式严重影响着树的准确性。分类树和回归树的分割判定准则有所不同。

决策树使用多种算法来决定把一个节点分裂成两个或更多的子节点。子节点的生成使得分裂后的各个子节点的纯度增加。决策树在所有可用变量上进行分裂，然后选择使得分裂后节点的纯度最高的分裂方式。

算法的选择基于目标变量的数据类型。让我们来看一下决策树中最常用的四种算法：

基尼系数（Gini Index）

基尼系数指出：我们从总体中随机挑选两个样本，如果总体是纯的，那么这两个样本是同类别的概率为1。

1. 用于处理分类型目标变量“Success”或者“Failure”。
2. 它只作用于二进制分裂。
3. 基尼系数越大，纯度越高。
4. CART（分类和回归树）使用Gini方法创建二进制分裂。

如何计算一个分裂的基尼系数？

1. 计算各个子节点的基尼系数：计算Success和Failure的概率的平方和：$p^2 + q^2$。
2. 计算分裂的基尼系数：计算各个子节点基尼系数的加权平均值。

例子：引用上面的例子，我们想要根据目标变量（是否打板球），对学生进行划分。如下图：我们使用两个输入变量Gender和Class对总体进行分割。现在，我想用基尼系数来确定哪个分裂能够产生更均匀（纯）的子节点。

基于Gender进行分裂：

1. 计算子节点Female的基尼系数：(0.2)×(0.2)+(0.8)×(0.8)=0.68
2. 计算子节点Male的基尼系数：(0.65)×(0.65)+(0.35)×(0.35)=0.55
3. 计算Gender分裂的基尼系数：(10/30)×0.68+(20/30)×0.55=0.59

基于Class进行分裂：

1. 计算子节点Class IX的基尼系数：(0.43)×(0.43)+(0.57)×(0.57)=0.51
2. 计算子节点Class X的基尼系数：(0.56)×(0.56)+(0.44)×(0.44)=0.51
3. 计算Class分裂的基尼系数：(14/30)×0.51+(16/30)×0.51=0.51

可以看出，基于Gender分裂的基尼系数要高于基于Class分裂的基尼系数。因此，节点将基于Gender进行分裂。

卡方（Chi-Square）

它可以用来衡量子节点和父节点之间是否存在显著性差异。我们用目标变量的观测频率和期望频率之间的标准离差的平方和来计算卡方值。

1. 它用于处理分类型目标变量“Success”或“Failure”。
2. 它可以计算两个或多个分裂。
3. 卡方越高，子节点与父节点之间的差异越显著。
4. Chi-square = ((Actual – Expected)^2 / Expected)^1/2
5. 它生成的树称为：CHAID (Chi-square Automatic Interaction Detector)

如何计算一个分裂的卡方：

1. 通过计算Success和Failure的偏差来计算单个节点的卡方。
2. 通过计算每个节点的Success和Failure的所有卡方总和计算一个分裂的卡方。

例子：仍然采用上述的例子。

基于Gender分裂：

1. 首先，我们统计节点Female中“Play Cricket"和”Not Play Cricket“的学生数，分别为2和8。
2. 计算“Play Cricket"和”Not Play Cricket“的期望值，都是10 × 50% = 5。因为父节点中“Play Cricket"和”Not Play Cricket“的比例都是50%。
3. 计算离差值Actual - Expected。“Play Cricket”：2-5=-3；“Not Play Cricket”：8-5=3。
4. 计算节点“Play Cricket"和”Not Play Cricket“的卡方值：Chi-square = ((Actual – Expected)^2 / Expected)^1/2。都是1.34。
5. 和上述同样的方法计算Male节点的卡方值。
6. 将所有节点的卡方值求和，计算一个分割的卡方值。

基于Class分裂：

和上述计算过程相似，计算结果如下：

可以看出，基于Gender的分裂比基于Class的分裂更显著。

信息增益（Information Gain）

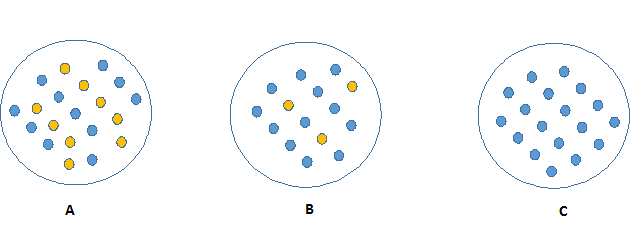
观察下面的图像，想一下哪个节点描述起来更加容易。答案一定是C，因为C图中的所有的值都是相似的，需要较少的信息去解释。相比较，B和A需要更多的信息去描述。用纯度描述，就是：Pure(C) > Pure(B) > Pure(A)。

纯度越高的节点，就会需要更少的信息去描述它；相反，不纯度越高，就会需要更多的信息。信息论用熵来定义系统的混乱程度。如果样本中的个体是完全相同类别的，那么系统的熵为0；如果样本是等划分的（50%-50%），那么系统的熵为1。

熵的计算公式为：Entropy = -p×log(p) - q×log(q), 其中log以2为底。如下图，当p=0.5时，熵最大，为1。

这里的p和q分别是节点中Success和Failure的概率。熵也用于分类型目标变量。它选择与父节点和其他分裂相比，拥有最低熵的分裂。熵越小越好。

如何计算一个分裂的熵？

1. 计算父节点的熵。
2. 计算分裂的每一个节点的熵，然后计算分裂下的所有子节点的加权平均熵。

例子：用信息熵的方法在学生打板球案例中挑选出最好的分裂。

1. 父节点的熵 = -(15/30)log2(15／30)-(15/30)log2(15/30) = 1。这里的1表示它是一个非纯节点。
2. Female节点的熵 = -(2/10)log2(2/10)-(8/10)log2(8/10)=0.72；Male节点的熵 = -(13/20)log2(13/20)-(7/20)log2(7/20)=0.93。
3. 基于Gender的分裂熵 = 所有子节点熵的加权平均 = (10/30)×0.72+(20/30)×0.93=0.86。
4. CLass IX节点的熵 = -(6/14)log2(6/14)-(8/14)log2(8/14)=0.99；Class X节点的熵 = -(9/16)log2(9/16)-(7/16)log2(7/16)=0.99。
5. 基于Class的分裂熵 = (14/30)×0.99+(16/30)×0.99=0.99。

可以看出，基于Gender分裂的熵更小。所以树将基于Gender进行分裂。我们可以计算信息增益为：1-Entropy。

方差削减（Reduction in Variance）

至此，我们已经讨论了很多关于分类型目标变量的算法。方差削减是用于连续型目标变量的算法（回归问题）。它使用方差公式去挑选最优分裂。方差最小的分裂将会作为分割总体的准则。

如何计算方差？

1. 计算每一个节点的方差。
2. 计算每一个节点方差的加权平均，作为一个分裂的方差。

例子：仍然使用打板球的例子。这里，我们将“Play Cricket”标记为1，“Not Play Cricket”标记为0。下面，利用方差的算法挑选出最优的分裂：

1. 根节点的方差。这里均值为：(15×1 + 15×0)/30 = 0.5。方差为：(15×(1-0.5)^2 + 15×(0-0.5)^2)/30=0.25。
2. Female节点的均值为：(2×1+8×0)/10=0.2。方差为：(2×(1-0.2)^2+8×(0-0.2)^2)/10=0.16。
3. Male节点的均值为：(13×1+7×0)/20=0.65。方差为：(13×(1-0.65)^2+7×(0-0.65)^2)/20=0.23。
4. 基于Gender分裂的方差为：(10/30)×0.16+(20/30)×0.23=0.21。
5. Class IX节点的均值为：(6×1+8×0)/14=0.43。方差为：(6×(1-0.43)^2+8×(0-0.43)^2)/14=0.24。
6. Class X节点的均值为；(9×1+7×0)/16=0.56。方差为：(9×(1-0.56)^2+7×(0-0.56)^2)/16=0.25。
7. 基于Class分裂的方差为：(14/30)×0.24+(16/30)×0.25=0.25。

可以看出，基于Gender分裂的方差更低，所以树将会选择Gender变量进行分裂。

至此，我们已经了解了决策树的一些基础知识，以及决策树如何选择最优变量进行分裂，建立树模型的。决策树可以处理回归以及分类问题，下面让我们详细了解这些方面。

4.模型建立的关键参数是什么？如何避免决策树的过拟合？

过拟合是建立决策树模型时面临的重要挑战之一。如果一个决策树没有限制条件，那么它会在训练集上给你100%的准确率。因为在决策树底部，每一个观察值都将会成为一个叶子节点。因此，建立决策树模型的时候防止过拟合至关重要。我们可以通过一下2种方式防止过拟合：

1. 限制树的大小。
2. 剪枝。

限制树的大小

可以通过定义树的各种参数，限制树的大小。首先，让我们看下决策树的一般结构：

用于定义树的参数在下面进一步解释。下面描述的参数与工具无关。理解参数在建立树模型中的作用是很重要的。当然，这些参数在R和Python中都可以设置。

1. 节点分裂的最小样本（Minimum samples for a node split）

   • 定义一个节点进行分裂要满足的最小样本量。
   • 用于控制过拟合。较高的值可以组织模型继续学习关系，这些关系可能只存在于一些特定的样本中。
   • 如果最小样本设置的过高，可能导致欠拟合。需要用CV进行调整。

2. 叶子节点的最小样本（Minimum samples for a terminal node (leaf)）

   • 定义叶子节点中，最小的样本量。
   • 和节点分裂的最小样本类似，用于控制过拟合。
   • 一般来说，在不平衡分类问题中应该选择较低的值，因为少类别的点落入的区域样本数将会更少。

3. 树的最大深度（Maximum depth of tree）

   • 一棵树的最大深度。
   • 用于控制过拟合。因为决策树越深就会导致模型学习与特定样本具有强相关的关系，使得泛化能力变弱。
   • 需要用CV进行调整。

4. 叶子结点的最大数量（Maximum number of terminal nodes）

   • 决策树中，叶子节点数量的最大值。
   • 可以代替树的最大深度（max_depth）。因为二叉树中，深度为'n'的树将最多生成2^n个叶子。

5. 分裂所考虑的最大特征数（Maximum features to consider for split）

   • 搜索最优分裂时所考虑的最大特征数。这些特征变量都是随机挑选的。
   • 根据经验法则，总特征数的平方根效果最佳。但是，我们应该检查高达30%-40%的总特征。
   • 较高的值可能导致过拟合，但是取决于实际案例。

剪枝（Tree Pruning）

如前所述，设置约束的技术是一种贪婪方法。换句话说，它将检查目前状态下的最优分裂并继续分裂，直到达到指定的终止条件。让我们考虑一下下面“当你正在开车的时候”的场景：

有两个车道：

1. 一个车道上的汽车以80km/h行驶。
2. 另一个车道上的卡车以30km/h行驶。

此时，你是黄色的车，你想超过前面两辆汽车，你将会有2个选择：

1. 从左侧迅速超过前面两辆汽车。
2. 继续在当前车道上行驶。

让我们来分析一下上面两种选择。在第一种选择中，你将会立即超过前面的两辆汽车到达卡车的后方，接下来以30km/h的速度行驶，然后等待机会回到右侧车道。但此时，原本在你后面的车将会你前方行驶。在第二种选择中，你将保持当前速度继续行驶，先超过卡车，然后视情况超越前面的车。

这正是正常决策树与剪枝之间的区别。带有约束的决策树不会看到前方的卡车，而是选择贪婪的方式，直接从左侧超车。相反，如果我们采取剪枝，将会先看看前面的几步，然后再进行有效的选择。

因此，我们知道了剪枝的效果将会更好。但是如何在决策树中实现剪枝呢？其实思想很简单。

1. 首先，我们先生成一个比较深的决策树。
2. 然后，从树的底部开始，移除和顶部相比增益为负的叶子。
3. 假如一个分裂的增益为-10，然后下一步分裂的增益为20。普通的决策树将会在步骤1时停止分裂。但是在剪枝中，将会保留这两个分裂，因为在整体上实现了+10的增益。

注意，sklearn中的决策树分类器目前不支持剪枝。比较先进的包，例如xgboost中采用了剪枝算法。但是在R的rpart包中，提供了剪枝的函数。恭喜R的用户们！

5.基于树的模型优于线性模型吗？

“如果我能够用逻辑回归处理分类问题，用线性回归处理回归问题，还有必要使用树模型吗？”我们中的很多人都会有这样的疑问。

事实上，你可以使用任何算法。它取决于你所处理的问题类型。让我们看看一些关键因素，这些因素将帮助您决定使用哪种算法：

1. 如果自变量和因变量能够很好地用线性模型近似，那么线性回归的性能将优于基于树的模型。
2. 如果自变量与因变量之间存在高度的非线性以及复杂的关系，那么基于树的模型性能将优于传统的回归算法。
3. 如果你想建立一个结果易于解释的模型，那么决策树将会做得更好。决策树模型比线性回归模型更易于解释。

6.在R和Python中使用决策树

对于R以及Pythn用户来说，很容易实现一个决策树模型。为了便于使用，我已经共享了标准代码，您只需要替换您的数据集名称和变量就可以使用了。

对于R用户，你可以使用很多包来实现决策树算法，例如ctree, rpart, tree等。

library(rpart)
x <- bind(x_train, y_train)

# 生成树
fit <- rpart(y_train ~ ., data = x, method='class')
summary(fit)
# 预测
predicted <- predict(fit, x_test)

在上面的代码中：

• y_train - 表示因变量。
• x_train - 表示自变量。
• x - 表示训练数据。

对Python用户，代码如下：

# 加载你能够用到的包，例如pandas, bumpy
from sklearn import tree
# 假设你已经准备好了X，y，以及x_test
# 创建树对象
model = tree.DecisionTreeClassifier(criterion='gini') #分类
# model = tree.DecisionTreeRegressor() #回归
# 训练模型
model.fit(X, y)
model.score(X, y)
# 预测
predicted = model.predict(x_test)

7.基于树的模型的集成方法（Ensemble Methods）是什么？

"集成“的就是”群“，”组“，”集合“的意思。集成算法将一组预测模型组合起来，以达到更精确，更稳定的预测效果。集成算法可以显著提高基于树模型的性能。
与其他模型一样，基于树的模型也遭受着偏倚和方差的困扰。偏倚是指：预测值和观测值的平均差异。方差是指：