问题引入
1.
.box1{
position: absolute;
top: 0;
left: 0;
width: 100px;
height: 50px;
background: black;
transform: rotate(45deg) translate(300px,300px) ;
}
.box2{
position: absolute;
top: 0;
left: 0;
width: 100px;
height: 50px;
background:black;
transform: translate(300px,300px) rotate(45deg) ;
}可以看到通过transform设置的translate和rotate,2个盒子由于先后顺序不同,但是差别却很大。
2.
.test{
width: 20px;
height: 140px;
background-color: salmon;
position: absolute;
top: 500px;
left: 500px;
transform: rotate(90deg);
transform: scale(0.5);
}
.test:hover
{
transform: rotate(45deg);
}
hover后:
可以看到 hover后transform: rotate(45deg); 使得一开始设置的scale恢复了初始值1。
由此可见,transform 是组件化的,其中的2D图像变化并不只是单纯的skew(),scale(),rotate(),translate()等
Matrix
matrix()
CSS 函数 matrix() 用六个指定的值来指定一个均匀的二维(2D)变换矩阵。这个矩形中的常量值是不作为参数进行传递的,其他的参数则在主要列的顺序中描述。
举个例子
transform: 'translate(tx,ty) rotate(a) skew(b) scale(sx.sy)'
代表将坐标系先 translate 然后 rotate 然后 skew 然后 scale 为新的坐标系。即新坐标系下的点先经过 scale 然后 skew 然后 rotate 然后 translate 后对应于老坐标系下的点。
那Matix是如何运算的呢?
引用文字
在笛卡尔坐标系中,每个 欧氏空间 里的点都由横坐标和纵坐标这两个值来确定。 在CSS(和大部分的计算机图形学)中,原点 (0, 0) 在元素的左上角。每个点都使用数学上的向量符号(x,y)来描述。
每个线性函数使用 2 × 2 矩阵描述,如:
[a c]
[b d]
将矩阵乘法用于上述坐标系中的每个点,一个变换就形成了:
可以在一行中进行多次矩阵乘法进行变换:
有了这种方法,就可以描述大部分常见的变换并因此可以将他们组合起来,如:旋转、缩放或拉伸。(事实上,所有线性函数的变换都可以被描述。)组合的变换是从右到左生效的。然而,有一种常见的变换并不是线性的,所以当这种变换要用这种方法来表示时,应该被单独列出来:位移。位移的向量 (tx, ty) 必须单独表示,作为两个附加参数。
而上面的例子可以写成
显而易见的
tranmsform的属性是由Matrix矩阵通过参数计算出来
计算方法
translate(tx,ty)
transform: matrix(1, 0, 0, 1, tx, tx)这两个是等价的 , 意味着translate的两个参数 ,被transform放到了第五个和第六个参数中计算。
同样的
scale(sx, sy)
matrix(sx, 0, 0, sy, 0, 0)这两个也是等价的
如果是旋转rotate(),则要用到三角函数
rotate(θ)
matrix(cosθ,sinθ,-sinθ,cosθ,0,0)
skew()则是使用tan()
skew(θ)
matrix(1,tan(θy),tan(θx),1,0,0)
再通过上面的矩阵相乘公式,可以算得Matrix函数参数值
问题1中,可以表达成
[1,0,300] [cos45°, -sin(45°) ,0]
[0,1,300] * [sin45°, cos45°, 0]
[0,0, 1 ] [ 0, 0 , 1]相反的 矩阵相乘不满足交换律, 当translate(300px,300px)和rotate(45deg)两个顺序互换的话,矩阵相乘算得结果参数不同, 所以对应的效果也会不同
问题2中
原本transform通过rotate和scale用2个矩阵相乘赋予了Matrix()函数参数
然而transform一旦再次设置rotate(),则会将Matrix()函数参数重置,
所以才会使得transform之前设置的属性荡然无存。
结语
原本CSS3的问题, 怎么就不知不觉变成线代问题了呢 - -



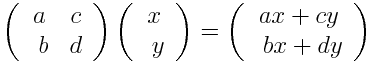


**粗体** _斜体_ [链接](http://example.com) `代码` - 列表 > 引用。你还可以使用@来通知其他用户。