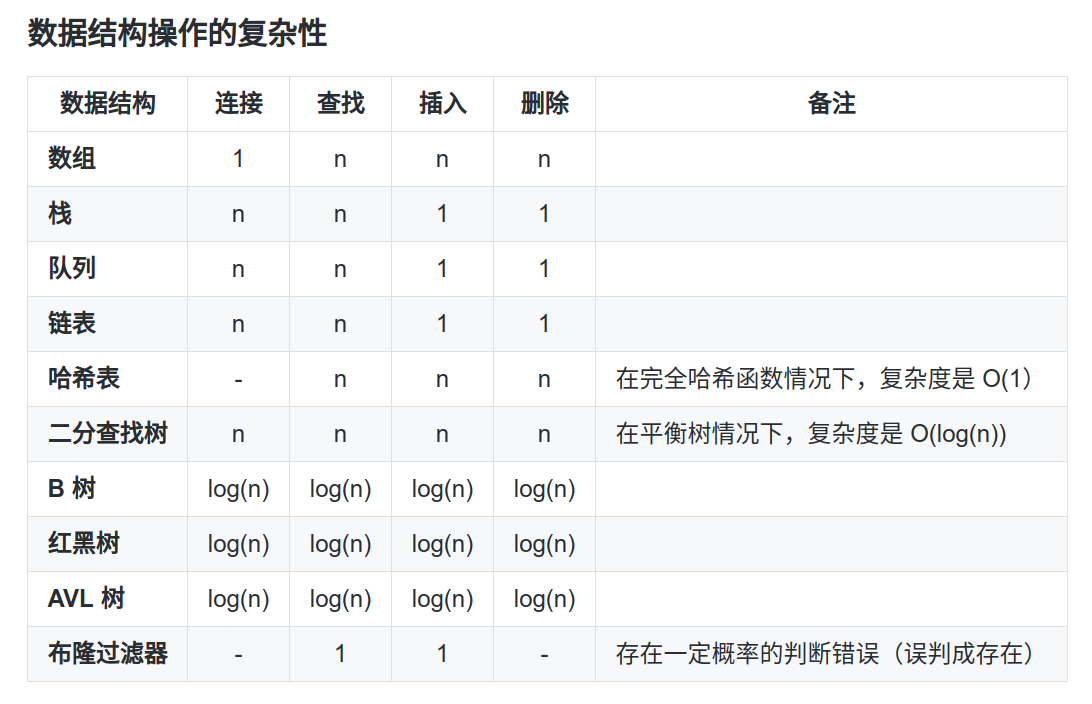
一、常见数据结构
简单数据结构(必须理解和掌握)
- 有序数据结构:栈、队列、链表。有序数据结构省空间(储存空间小)
- 无序数据结构:集合、字典、散列表,无序数据结构省时间(读取时间快)
复杂数据结构
- 树、 堆
- 图
二、本系列主要内容
数组和列表: 最常用的数据结构
- 与链表相比,数组具有更好的缓存位置。
- 数组具有随机访问的特点(
常用的二分查找算法需要用数组来存储数据。但如果我们选择链表这种数据结构,二分查找算法就无法工作了,因为链表并不支持随机访问。)
- 栈和队列: 与列表类似但是更复杂数据结构
链表: 如何通过它们克服数组的不足,
- 链表允许在迭代期间有效地从序列中的任何位置插入或删除元素。
- 链表的一个缺点是访问时间是线性的(而且难以管道化)。(更快的访问,如随机访问,是不可行的)
- 字典: 将数据以键-值对的的形式储存
- 散列(表): 适用于快速查找和检索
- 集合: 适用于存储只出现一次的元素
- 二叉树: 以层级的形式存储数据
- 图和图算法: 网络建模的理想选择
- 算法:包括排序、搜索、图形算法
- 高级算法: 动态规划、贪心算法、BF、分治、回溯等算法范式
- 加密算法:
有序数据结构
数组
列表
栈
队列
链表
数组与链表的对比
- 内存的分配方式不同: 由于数组具有连续性,需要开辟一段连续内存空间(前提是系统得有足够得连续内存供使用,因此要求比较高),而链表则可充分利用离散的内存,根据指针“串联”起来,灵活度更高,但相比数组更占内存空间;
时间复杂度不同:插入、删除等操作,数组为保证连续性,为 O(n),而链表则为 O(1),随机访问操作,数组只需 O(1),而链表需要 O(n)
无序列数据结构
集合
字典
散列(表)
简单算法 => 二分查找
二分查找是搜索算法中的一种,用来搜索有序数组
二分查找:是一种简单算法,其输入是一个有序的元素列表(必须有序的原因稍后解释)。如果要
查找的元素包含在列表中,二分查找返回其位置;否则返回null。
Javascript ES6实现
非递归的
/**
* 函数binarySearch接受一个有序数组和一个元素。 如果指定的元素包含在数组中, 这个
函数将返回其位置。 你将跟踪要在其中查找的数组部分—— 开始时为整个数组。
*/
const binarySearch = (list, item) => {
// 数组要查找的范围
// low、high用于跟踪要在其中查找的列表部分
let low = 0
let high = list.length - 1
while(low <= high) { // 只要范围没有缩小到只包含一个元素
const mid = Math.floor((low + high) / 2)
const guess = list[mid] // 找到中间的元素
if(guess === item) { // 找到元素
return mid
}
if(guess > item) { // 猜测的数大了
high = mid - 1
} else { // 猜测的数小了
low = mid + 1
}
}
return null
}
const myList = [1, 3, 5, 7, 9]
console.log(binarySearch(myList, 3))
console.log(binarySearch(myList, -1))递归的
const binarySearch = (list, item, low, hight) => {
let arrLength = list.length
while (low <= high) {
let mid = Math.floor((low + high) / 2)
let guess = list[mid]
if( guess === item ) {
return mid
} else if (guess > item) {
high = mid - 1
list = list.slice(0, mid)
return binarySearch(list, item, low, high)
} else {
low = mid + 1
list = list.slice(low, arrLength)
return binarySearch(list, item, low, high)
}
}
return null
}
const createArr = (n) => Array.from({length: n}, (v, k) => k + 1)
const myList = createArr(100)
let low = 0
let high = myList.length - 1
console.log(binarySearch(myList, 3, low, high))
console.log(binarySearch(myList, -1, low, high))找一个平衡二叉树最后一个节点
Python实现
四、运行时间(时间复杂度)
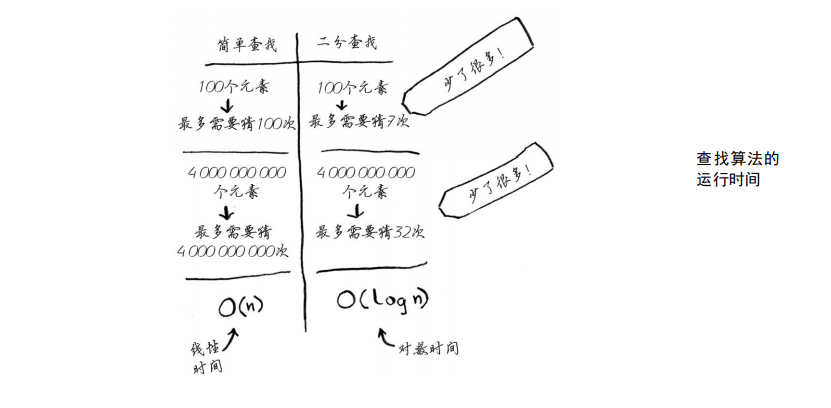
二分查找的运行时间为对数时间(或log时间)。
如果列表包含100个元素,最多要猜7次;如果列表包含40亿个数字,最多
需猜32次。
即: 2的7次方 = 100
简单查找时间是 y= ax 的线性方方程
所以很容易得出结论
随着元素数量的增加(x增加),二分查找需要的时间(y)并不多, 而简单查找需要的时间(y)却很多。
因此,随着列表的增长,二分查找的速度比简单查找快得多。
为检查长度为n的列表,二分查找需要执行log n次操作。使用大O表示法,
这个运行时间怎么表示呢?O(log n)。一般而言,简单算法的大O表示法像下面这样
三、什么是复杂度分析?
1.数据结构和算法解决是“如何让计算机更快时间、更省空间的解决问题”。
2.因此需从执行时间和占用空间两个维度来评估数据结构和算法的性能。
3.分别用时间复杂度和空间复杂度两个概念来描述性能问题,二者统称为复杂度。
四、为什么要进行复杂度分析?
1.和性能测试相比,复杂度分析有不依赖执行环境、成本低、效率高、易操作、指导性强的特点。
2.掌握复杂度分析,将能编写出性能更优的代码,有利于降低系统开发和维护成本。
五、如何进行复杂度分析?
1.大O表示法
1)来源
算法的执行时间与每行代码的执行次数成正比,用T(n) = O(f(n))表示,其中T(n)表示算法执行总时间,f(n)表示每行代码执行总次数,而n往往表示数据的规模。
2)特点
以时间复杂度为例,由于时间复杂度描述的是算法执行时间与数据规模的增长变化趋势,所以常量阶、低阶以及系数实际上对这种增长趋势不产决定性影响,所以在做时间复杂度分析时忽略这些项。
2.复杂度分析法则
1)单段代码看高频:比如循环。
2)多段代码取最大:比如一段代码中有单循环和多重循环,那么取多重循环的复杂度。
3)嵌套代码求乘积:比如递归、多重循环等
4)多个规模求加法:比如方法有两个参数控制两个循环的次数,那么这时就取二者复杂度相加。
5.1 大O符号
大O符号中指定的算法的增长顺序
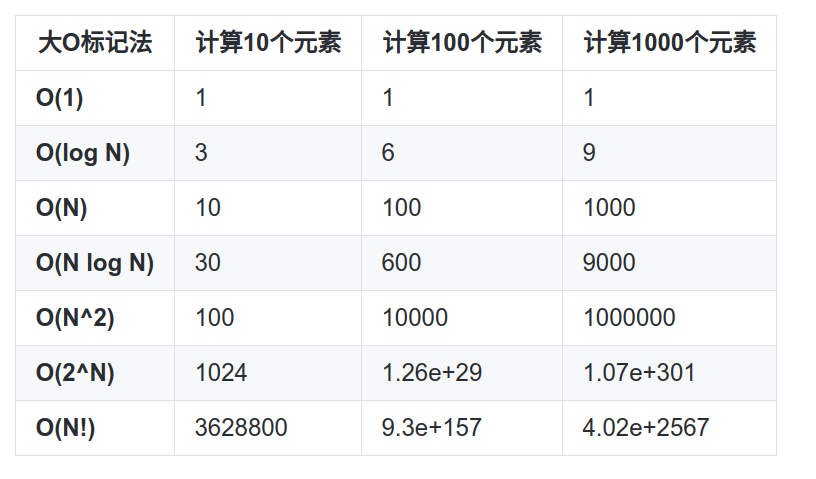
以下是一些最常用的 大O标记法 列表以及它们与不同大小输入数据的性能比较。
- O(log n),也叫对数时间,这样的算法包括二分查找
- O(n),也叫线性时间,这样的算法包括简单查找。
- O(n * log n),这样的算法包括
快速排序——一种速度较快的排序算法。 ,这样的算法包括
选择排序——一种速度较慢的排序算法- O(n!),这样的算法包括接下来将介绍的旅行商问题的解决方案——一种非常慢的算法
五、常用的复杂度级别?
多项式阶:随着数据规模的增长,算法的执行时间和空间占用,按照多项式的比例增长。包括,
O(1)(常数阶)、O(logn)(对数阶)、O(n)(线性阶)、O(nlogn)(线性对数阶)、O(n^2)(平方阶)、O(n^3)(立方阶)
非多项式阶:随着数据规模的增长,算法的执行时间和空间占用暴增,这类算法性能极差。包括,
O(2^n)(指数阶)、O(n!)(阶乘阶)
六、 空间复杂度分析
时间复杂度的全称是渐进时间复杂度,表示算法的执行时间与数据规模之间的增长关系。类比一下,空间复杂度全称就是渐进空间复杂度(asymptotic space complexity),表示算法的存储空间与数据规模之间的增长关系
六、小结
如何掌握好复杂度分析方法?
复杂度分析关键在于多练,所谓孰能生巧
- 算法的速度指的并非时间,而是操作数的增速。
- 谈论算法的速度时,我们说的是随着输入的增加,其运行时间将以什么样的速度增加。
- 算法的运行时间用大O表示法表示。
O(log n)比O(n)快,当需要搜索的元素越多时,前者比后者快得越多
快速排序
快排和二分查找都基于一种叫做「分治」的算法思想,通过对数据进行分类处理,不断降低数量级,实现
O(logN)(对数级别,比O(n)这种线性复杂度更低的一种,快排核心是二分法的O(logN),实际复杂度为O(N*logN))的复杂度。
快排大概的流程是:
- 随机选择数组中的一个数 A,以这个数为基准
- 其他数字跟这个数进行比较,比这个数小的放在其左边,大的放到其右边
- 经过一次循环之后,A 左边为小于 A 的,右边为大于 A 的
- 这时候将左边和右边的数再递归上面的过程
javascript实现
python 实现
def quicksort(array):
less = []; greater = []
if len(array) <= 1:
return array
pivot = array.pop()
for x in array:
if x < = pivot: less.append(x)
else: greater.append(x)
return quicksort(less) + [pivot] + quicksort(greater)旅行商问题--复杂度O(n!)的算法
简单的讲如果旅行者要去5个城市,先后顺序确定有5*4*3*2*1 = 120种排序。(这种排序想想高中时候学到过的排序知识)
推而广之,涉及n个城市时,需要执行n!(n的阶乘)次操作才能计算出结果。因此运行时间
为O(n!),即阶乘时间。除非涉及的城市数很少,否则需要执行非常多的操作。如果涉及的城市
数超过100,根本就不能在合理的时间内计算出结果——等你计算出结果,太阳都没了。
这种算法很糟糕!,可别无选择。这是计算机科学领域待解的问题之一。对于这个问题,目前还没有找到更快的算法,有些很聪明的人认为这个问题根本就没有更巧妙的算法。
面对这个问题,我们能做的只是去找出近似答案。
最后需要指出的一点是,高水平的读者可研究一下二叉树
关于二叉树,戳这里: 数据结构与算法:二叉树算法
七、常见练习
在一个二维数组中,每一行都按照从左到右递增的顺序排序,每一列都按照从上到下递增的顺序排序。请完成一个函数,输入这样的一个二维数组和一个整数,判断数组中是否含有该整数。
参考
算法图解
JavaScript 算法与数据结构
https://github.com/egonSchiel...
【算法】时间复杂度
【算法】空间复杂度
InterviewMap 时间复杂度
https://github.com/trekhleb/j...
每周一练 之 数据结构与算法(Stack)
All Algorithms implemented in Python



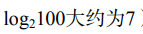







**粗体** _斜体_ [链接](http://example.com) `代码` - 列表 > 引用。你还可以使用@来通知其他用户。