【算法】算法图解笔记_快速排序

分而治之

分而治之(divide and conquer,D&C)是一种著名的递归式问题解决方法。
只能解决一种问题的算法毕竟用处有限,而D&C提供了解决问题的思路,是另一个可供你使用的工具。

D&C算法是递归的。使用D&C解决问题的过程包括两个步骤。
(1) 找出基线条件,这种条件必须尽可能简单。
(2) 不断将问题分解(或者说缩小规模),直到符合基线条件。

例1

假设你是农场主,有一小块土地。如何将一块地均匀地分成方块,并确保分出的方块是最大的呢?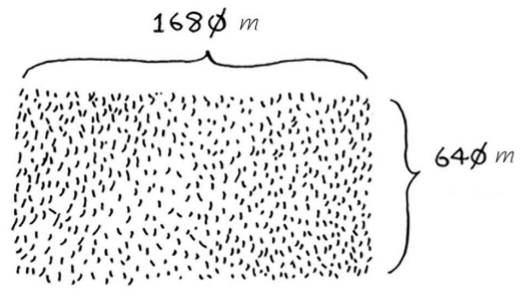

基线条件

最容易处理的情况是,一条边的长度是另一条边的整数倍。比如，25m x 50m的土地可以分成 2 个 25m x 25m 的方块。

递归条件

根据D&C的定义,每次递归调用都必须缩小问题的规模。首先找出这块地可容纳的最大方块。如，上图可以划出两个640 m × 640 m的方块,同时余下一小块400m x 640m 地。
我们下一步要做的就是对余下的那一小块地使用相同的算法。因为适用于这小块地的最大方块,也是适用于整块地的最大方块。换言之,你将均匀划分1680 m × 640 m土地的问题,简化成了均匀划分400m x 640 m土地的问题!

我们很容易实现上述过程。我们进一步抽象，这个过程实际上就是求两个整数的最大公倍数。

例2

给定一个数字数组，如，[2,4,6]，怎么返回这些数字相加后的结果。使用循环可以很容易实现。那使用递归怎么实现呢？

基线条件

最简单的数组不包含任何元素或只包含一个元素,这个可以认为是数组的基线条件。

递归条件

每次递归调用都必须离空数组更近一步。我们通过下面的等式缩小问题的规模。
sum [2,4,6] == 2 + sum [4,6]

使用Haskell可以很容易实现：

sum [] = 0
sum (x:xs) = x + (sum xs)

快速排序

快速排序是一种常用的排序算法,如，C语言标准库中的函数qsort实现的就是快速排序。

基线条件

数组为空或只包含一个元素。在这种情况下,只需原样返回数组。

递归条件

我们从数组中选择一个元素作为基准值（pivot），然后以该值为基准对数据分区（partitioning），这样数组划分成了三部分：

1. 一个由所有小于基准值的数字组成的子数组;
2. 基准值
3. 一个由所有大于基准值的数组组成的子数组。

这样问题缩小到了子数组规模。再分别对子数组应用以上过程，得到排序后的子数组，最终我们只要将这三部分拼接起来就能得到完全排序的数组。

注意：为了实现简单，基准值每次都取的数组首元素。

代码如下：

# python
def quicksort(array):
  if len(array) < 2:
    return array
  else:
    pivot = array[0]
    less = [i for i in array[1:] if i <= pivot]
    greater = [i for i in array[1:] if i > pivot]
    return quicksort(less) + [pivot] + quicksort(greater)

--haskell
import Data.List

quickSort :: Ord a => [a] -> [a]
quickSort [] = []
quickSort (x:xs) = quickSort lhs ++ [x] ++ quickSort rhs
  where
    (lhs, rhs) = partition (< x) xs

注意：上面的版本每次都新生成子数组，有些人认为正确的快速排序应该使用in-place交换，所以上面的算法不“正宗”。

再谈大 O 表示法

快速排序的独特之处在于,其速度取决于选择的基准值。在平均情况下,快速排序的运行时间为O(nlog n),在最糟情况下,退化为O(n2)。还有一种合并排序(merge sort)的排序算法，其运行时间为O(nlogn)。

大O表示法体现出的是对元素规模n的增速，但处理每个元素的速度是有差异的，比如，对每个元素执行(*2)和(+3).(*2)操作，明显是后者执行的时间长。
快速排序和合并排序的算法速度分别表示为c1 nlogn和c2 nlogn，c是算法所需的固定时间量,被称为常量。通常不考虑这个常量,因为如果两种算法的大O运行时间不同,这种常量将无关紧要。但有时候,常量的影响可能很大,对快速查找和合并查找来说就是如此。快速查找的常量比合并查找小,因此如果它们的运行时间都为O(n log n),快速查找的速度将更快。实际上,快速查找的速度确实更快,因为相对于遇上最糟情况,它遇上平均情况的可能性要大得多。