平衡二叉树——AVL

AVL

之前写过的二叉排序树（BST）在插入、删除和查找等基本操作的平均时间为O(logN)，但在最坏的情况下，这些基本运算的时间均会增至O(n)（因为退化成了链表）。为了避免这些情况发生，人们研究了许多种动态平衡的方法，使得在树中插入或删除元素时，通过调整树的形态来保持树的“平衡”，使之既保持BST的性质不变又保证树的高度在任何情况下均为O(logN)，从而确保树上的基本运算在最坏情况下的时间也均为O(logN)。下面的AVL就是这样的平衡树。

AVL 树是一种平衡二叉树，得名于其发明者的名字（ Adelson-Velskii 以及 Landis）。平衡二叉树递归定义如下：

1. 左右子树的高度差小于等于 1。
2. 其每一个子树均为平衡二叉树。

基于两点，我们就可以进行判断其一棵树是否为平衡二叉树了。

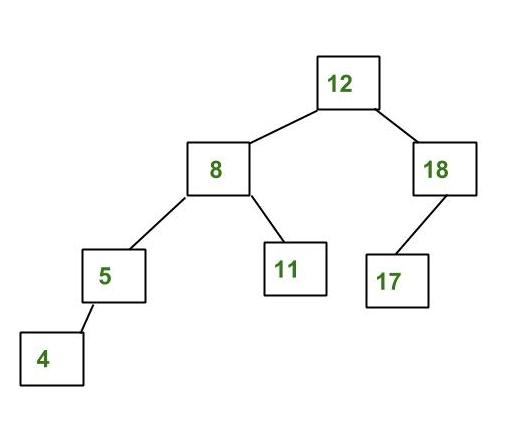
一个AVL树的例子

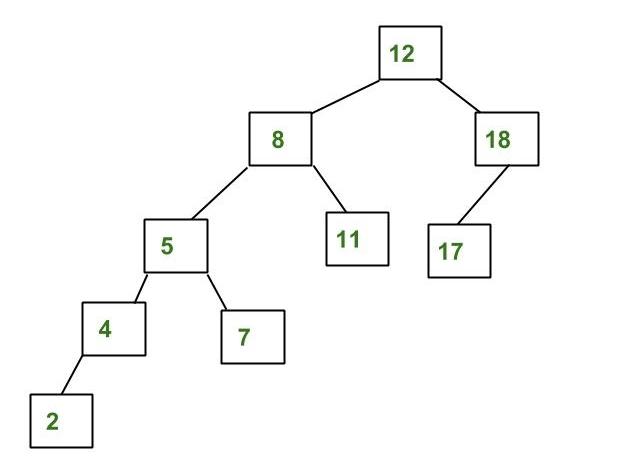
一个不是AVL树的例子

因为节点8的子树之差大于为2

实现原理

算法通过平衡因子（balaced factor，用bf表示）来具体实现上述平衡二叉树的定义。平衡因子的定义：平衡二叉树中每个节点有一个平衡因子，每个节点的平衡因子是该节点的左子树高度减去右子树的高度。从平衡因子的角度说，若一棵二叉树中所有节点的平衡因子的绝对值都小于等于1，即平衡因子取值为0、1或-1，则该二叉树为平衡二叉树。
用C语言定义该节点为：

typedef struct node
{
    KeyType key;
    int bf;   // 平衡因子
    InfoType data;
    struct node *lchild, *rchild;    
} BSTNode;

插入调整

若向平衡二叉树插入一个新节点后破坏了平衡二叉树的平衡性，首先从该新插入节点向根节点方向找到第一个失去平衡的节点，然后以该失衡节点和它相邻的刚查找过的两个节点构成调整子树，使之成为新的平衡子树。
失去平衡的最小子树是指以离插入节点最近，且平衡因子绝对值大于1的节点作为根节点的子树。调整该子树有以下四种情形：

(1) LL型调整

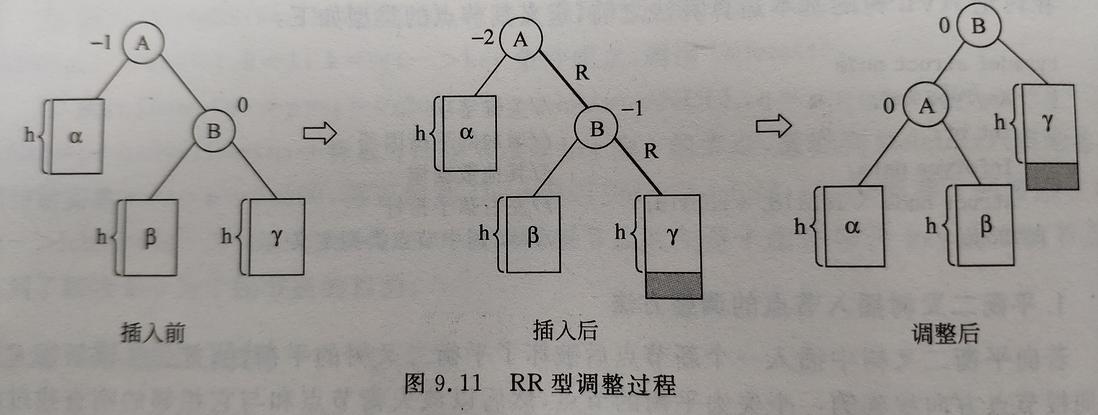
(2) RR型调整

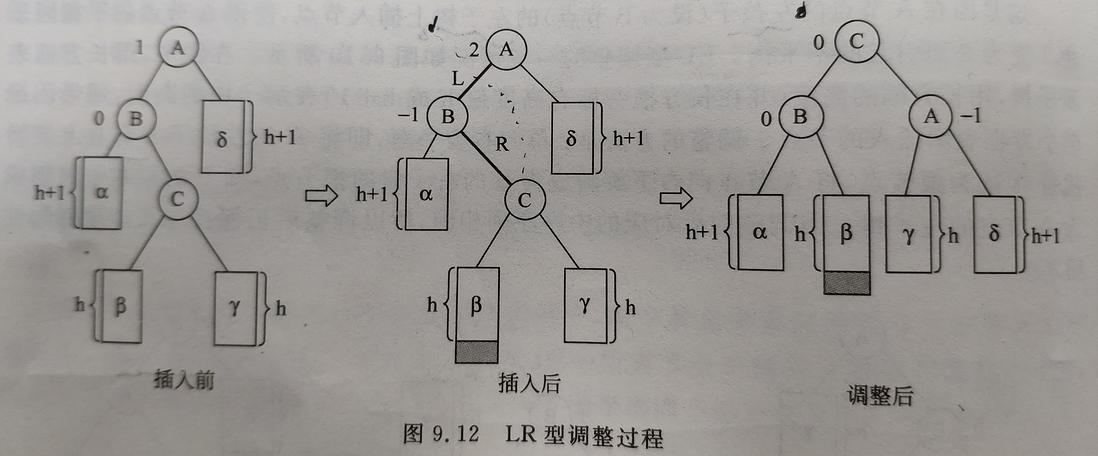
(3) LR型调整

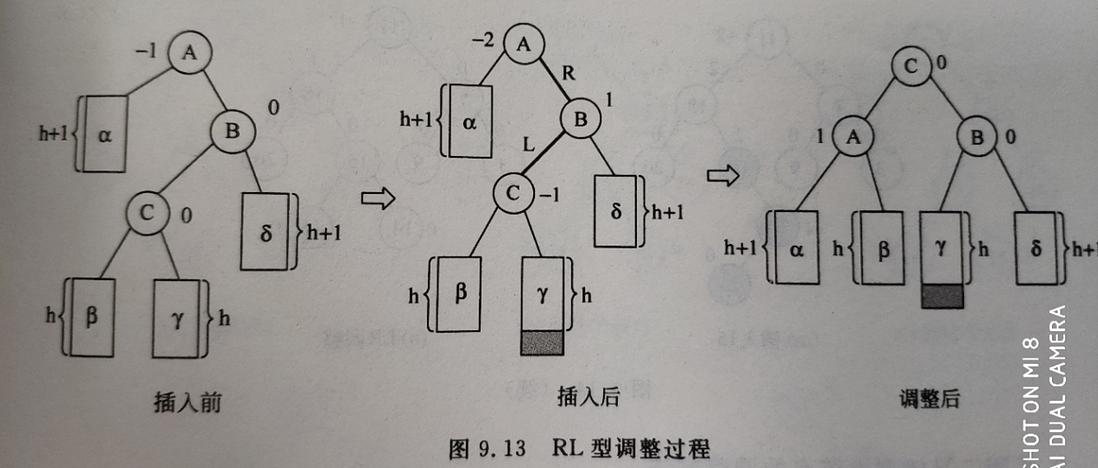
(4) RL型调整