前言
近几年时不时爆出养老保险空缺的新闻,搞得人心惶惶的。这不,把我1个挺要好在一线城市的异性朋友吓坏了。于是在微信上给我发了这样个截图,
并顺口问了我那么一句,它的收益真的有那么高吗?
对于这么好的机会,我怎么能轻易放过。于是耐心解答了一番,稍加整理后就有了这篇文章。
在这张截图中可以看到,如果每月投入500块,一直坚持到60岁,如果收益率为8%,那么到时累积的养老金大约就有83万。其中本金19.2万,而收益却高达63.5万,是本金的3.3倍。
现值与未来现值
实际上关于养老金这个问题,在金融学中只能算是个很简单的问题。当然它与我们的生活息息相关,毕竟没有人希望自己老无所依。
在金融数学模型中,通过用PV(Present Value)表示现值,而用FV表示未来现金的现值(Future Value)。换句话说,就是5年后的100块等价于当前的多少钱?
金融家们给出了这样1个数学公式(公式1):
如果觉得这个公式很陌生,那么我们将上述公式进行如下的修改或许你就会觉得挺眼熟的:
有没有发现它就是我们中学时代学过的存款的例子。比如,你在2015年存入余额宝1万块,假设每年年收益率为3%,那么2019年你的总收益是多少?
我们可以很容易通过计算器计算得到如下的结果:
>>> 10000 * (1+0.03) ** 4
11255.0881相比存入余额宝是正向的收益,由于通货膨胀的存在,你的财富开始逐渐贬值。因此,上述第1个公式中的R可以看作是每期的通货膨胀率,比如熟知的CPI。
如果我们假设每年的通货膨胀率是2%,那么当前的100块在5年后就相当于当前的90.57元:
>>> round(100 / (1+0.02) ** 5, 2)
90.57最近在招行APP上看到有篇《现在多少钱能和以前万元户持平?》的文章,不过作者是用CPI和M2进行计算。
年金
但是上述计算方法只适用于单次投入的情况,并不适用多次存入的情况。于是金融学家们又抛出了1个新的公式3:
这个公式看起来比之前第2个公式那个还复杂,实际上也只是个中学的水平。
在年金这个模型里,年金是指在未来n个时间段每期等额的现金支付。还是之前支付宝的例子,如果我每年初都存入1万块,那么2018年末我能拿到多少钱呢?接下来你就知道了。
在上述公式中,PMT是每期存入的定额现金,于是就有:
2015年末= 10000
2016末= 10000 + 10000 * 1.03
2017末= 10000 + 10000 * 1.0609 + 10000 * 1.03
2018末= 10000 + 10000 * 1.092727 + 10000 * 1.0609 + 10000 * 1.03
于是到2018年末我的支付宝里面将有41836.27元,当然代入上述公式就直接算出来了。
实际上,这里需要用到了中学学到的等比数列求和公式(公式4)
我们将第2个公式代入公式4中就可以很容易推算出公式3。
养老金中的收益
既然在上面我们已经知道了定投收益的计算公式,那么现在我们将其代入。假设你当前为28岁,那么到60岁退休还有32年,于是就有:
>>> PMT = 500
>>> R = 0.08 / 12
>>> n = (60-28) * 12由于我们是每月都投入500块,而年收益率假设为8%,那么月收益率自然就是8%/12=0.67%。
于是我们有:
>>> FV = (PMT / R) * ((1+R)**n-1)
>>> round(FV,2)
887758.98通过Python可以看到,等你退休的时候将有88.7万,而总投入是500×384=19.2万。
结语
经过一系列的计算,虽然计算结果与原来有所出入,但是由于存在一些额外的费用,如申购费等,实际的结果还比计算中的要少,对于上面的例子发现每年收益率为7.7%则与提供的内容基本一致。




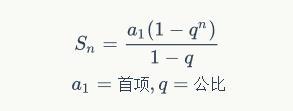
**粗体** _斜体_ [链接](http://example.com) `代码` - 列表 > 引用。你还可以使用@来通知其他用户。