【重学数据结构与算法(JS)】字符串匹配算法(二)——KMP算法

前言

在上一篇文章字符串匹配算法(一)——BF算法提到过，字符串匹配的思路是固定的：

1. 将模式串和主串进行比较

   • 从前往后比较
   • 从后往前比较
2. 匹配时，比较主串和模式串的下一个位置

3. 失配时,

   • 在模式串中寻找一个合适的位置

     • 如果找到，从这个位置开始与主串当前失配位置进行比较
     • 如果未找到，从模式串的头部与主串失配位置的下一个位置进行比较
   • 在主串中找到一个合适的位置，重新与模式串进行比较

优化在于其中的步骤，而KMP算法，就是优化第3步失配时寻找模式串合适位置的操作。

算法介绍和分析

那么如何寻找模式串中所谓合适的位置呢？可以先来看个栗子：

......

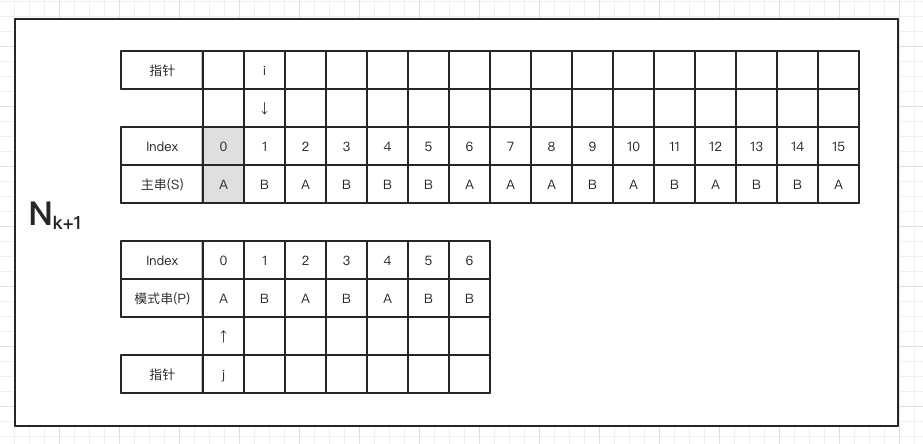
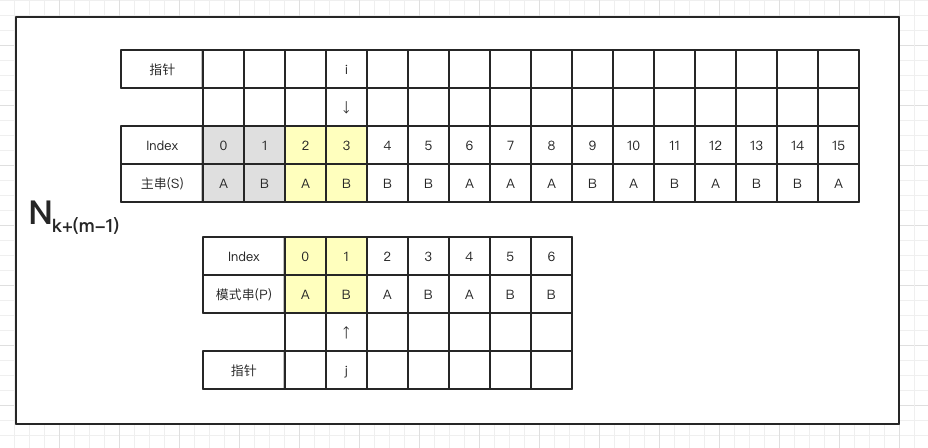
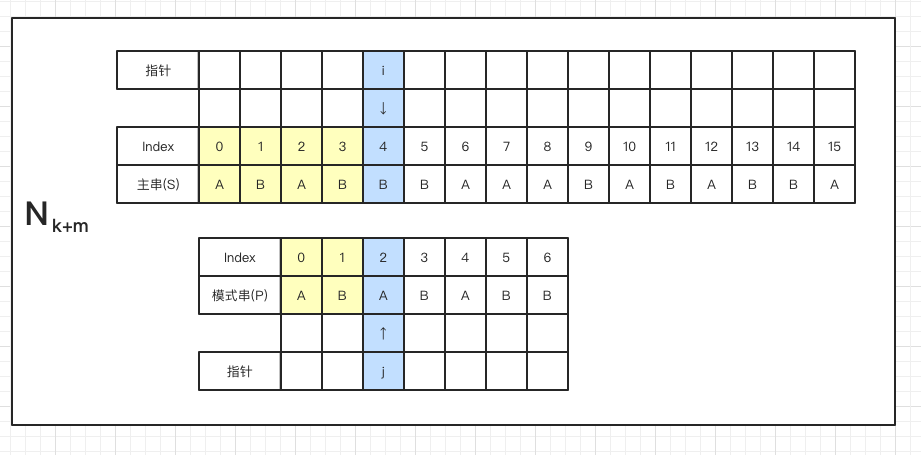
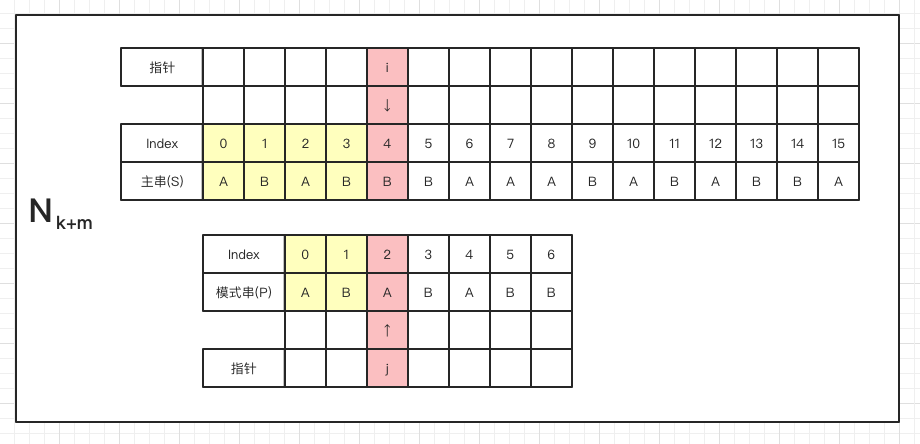
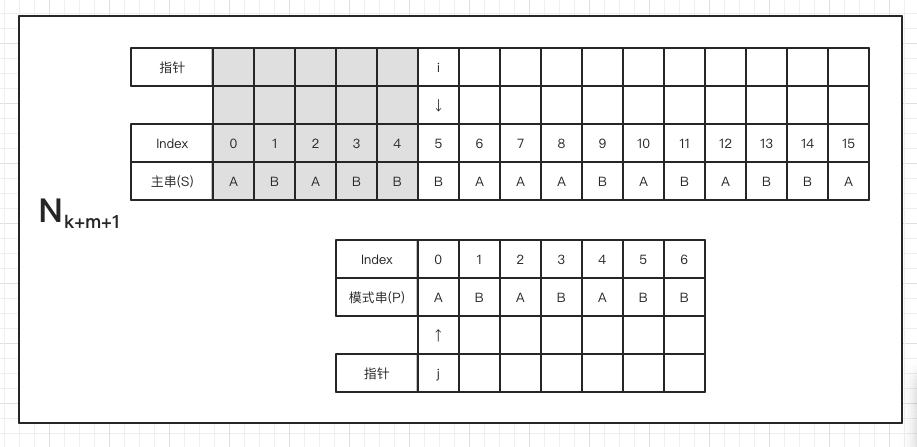
上面是 BF 匹配过程中从N_k到N_k+m的 m 次匹配过程，从中我们可以发现，从第 k 步到第 k+m 步时，指针 i 和 j 又回到了相同的位置，且 第 k+m 步 更具有匹配的可能性，所以我们思考一下，是不是可以由第 k 步直接跳到第 k+m 步呢？如果可以，就可以减少 m-1 次比较，大大提升效率。再进一步思考，如果将整个匹配过程再看作是重复地由N_k直接到N_k+m的推进，那么每次重复时，模式串开始比较的位置就是我们所要找的合适的位置。

如何寻找这些位置呢？我们可以把这个问题转化为求next数组的过程。

求 next 数组

我们再仔细观察下 N_k 和 N_k+m 两个状态

由于 N_k 状态下，模式串与主串具有完全匹配的部分，且要达到 N_k+m 状态所需移动到的位置信息也存在于匹配的部分，因此我们可以无视掉主串，只看模式串即可得到next数组。

再认真观察我们还能发现，N_k 状态不匹配时，N_k+m 状态本质上是将模式串中的另外一对 AB 和 主串 达成之前的已匹配状态。所以求next数组的问题又可以转化为当m位置不匹配时，求m位置之前的子串的最大相同前后缀的问题。

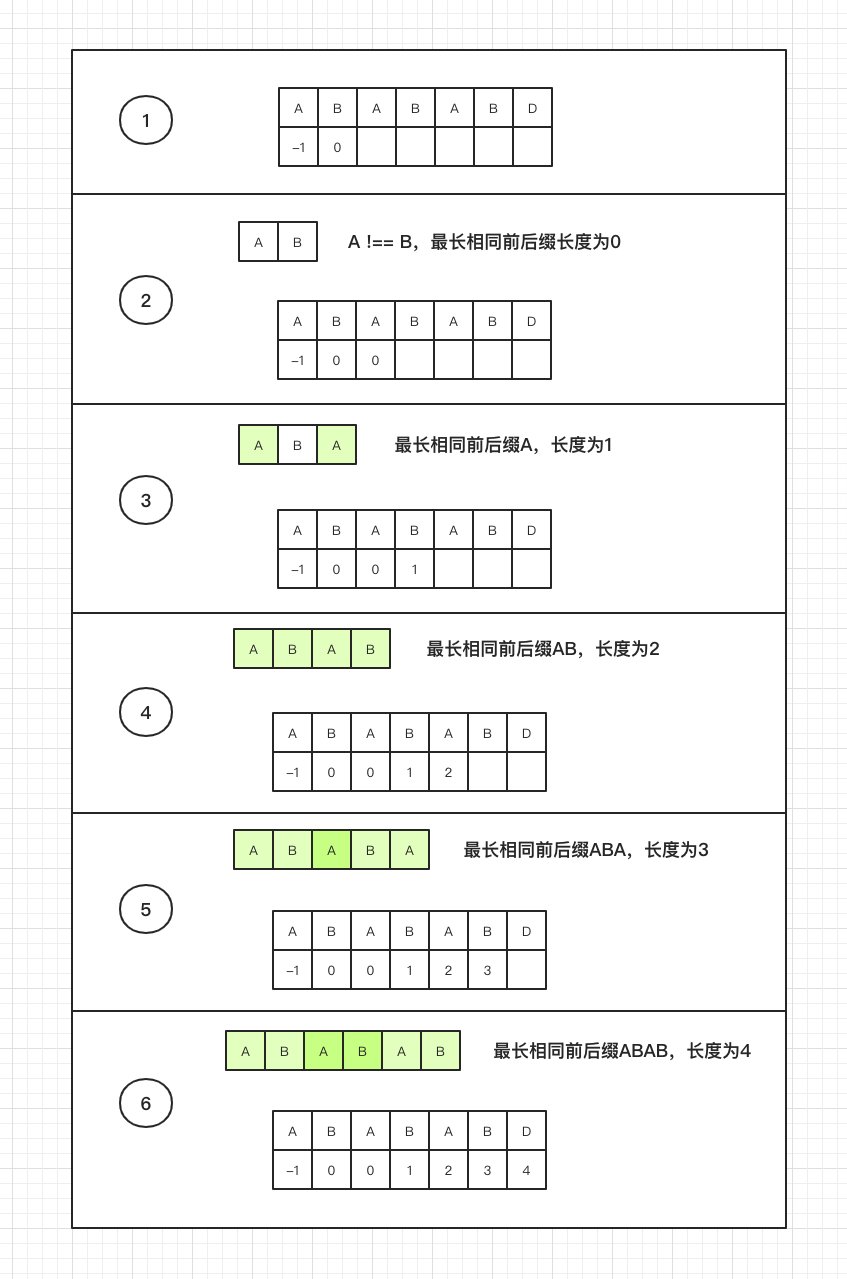
首先要建立一个规则，具有前后缀的字符串长度至少为2，所以我们定义如果长度为0，则对应next数组值为-1，如果长度为1，值为0。下面举个栗子：

ABABABD

手工求这么看其实没什么难度，自己多写几个串练一遍就会了。

代码

学会如何手工求next数组之后，整个KMP算法的代码如何写呢？
还记得最开始提到要记住的一点吗？匹配思路是一样的，只是优化了失配后的操作。根据这一点，我们可以把BF算法的框架先搬过来：

这样是不是可以接下来去补全 getNext() 方法就可以了呢？我们来看一个特殊情况：

当处在N_k+m状态时，发现失配位置前的 AB 没有最长公共前后缀，于是只能退回到BF算法的做法，也就是i++;j=0。但是这和我们上面的框架代码不符，需要进行改造：

• 每当 j = next[j] === -1 时，也需要进入第一个分支，使得 i++;j++(-1 + 1 = 0），变相达到效果。

得到最终的框架代码：

接下来就是进行对next数组的求解——完善 getNext()。这时候有的同学可能就会想对上述手工求法进行代码转化，可是万一模式串很长的话，那么这个时间复杂度就会变得相当的高，所以需要采用迭代法，利用每次所得的结果来求下一个结果，从而拼凑出next数组。

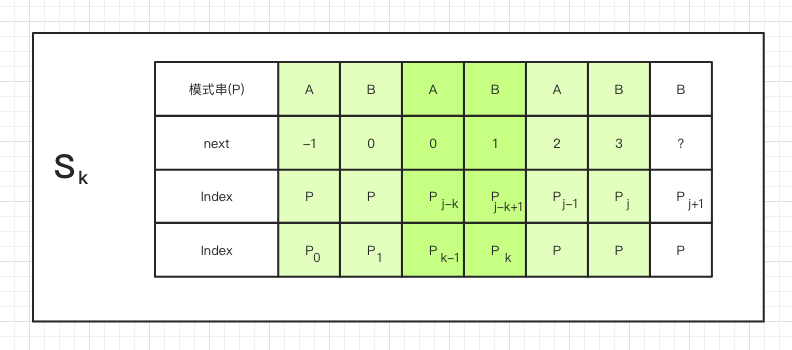
我们假设某一时刻有一个状态S_k

此时我们已经求完了next[j]的值，如何去求next[j+1]呢？仔细观察状态图，发现：

• 若P_k === P_j，则 P_j+1 前有next[j] + 1 = 4个相同的前后缀 P₀P₁P_k-jP_k 和 P_j-kP_j-k+1P_j-1P_j，也就是 next[j+1] = next[j] +1 = k + 1

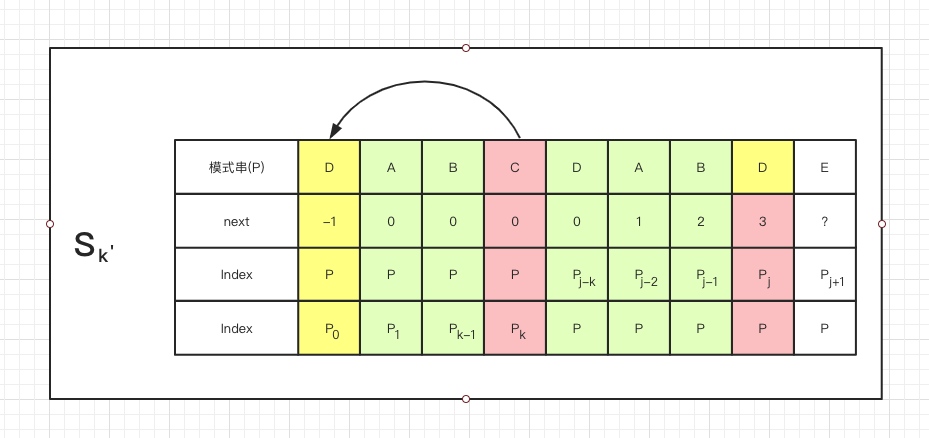
再来看一个状态

同样是求完了next[j]的值，

• 若P_k === P_j，对比 P_next[k] 是否 等于 P_j；如果 P_nextⁿ[k] === P_j，则next[j+1] = P_nextⁿ[k] + 1 = k + 1

如果 P_nextⁿ[k] !== P_j呢？

可以看到，

• 如果P_nextⁿ[k] !== P_j，则不断地递归前缀索引 k = next[k] 直到回到前缀第一个位置，则表示没有相同的前后缀，此时 j = -1，则 next[j+1] = P_nextⁿ[k] + 1 = k + 1 = 0

根据以上分析，我们可以补充完 getNext()

再优化一下写法

至此，一个完整的KMP算法就写好了。

思考是否还有优化的空间

我们来看一个特殊的例子：

这是一个前缀相同的一个模式串，且我们已经求得了next数组，接下来我们模拟一下上面写好的程序进行的操作：

1. j = 5，needle[5] !== haystack[i]；next[j] = 4，j = next[j];
2. j = 4，needle[4] !== haystack[i]；next[j] = 3，j = next[j];
3. j = 3，needle[3] !== haystack[i]；next[j] = 2，j = next[j];
4. j = 2，needle[2] !== haystack[i]；next[j] = 1，j = next[j];
5. j = 1，needle[1] !== haystack[i]；next[j] = 0，j = next[j];
6. j = 0，needle[0] !== haystack[i]；next[j] = -1，j = next[j];
7. j = -1, j++;i++;

我们发现由于前缀都是相等的，当第1步发现失配时，直接 j = -1 就可以了，也就是 next[5] = -1 即可。所以，优化点其实是体现在对next数组的优化，我们称之为nextVal数组

求nextVal数组

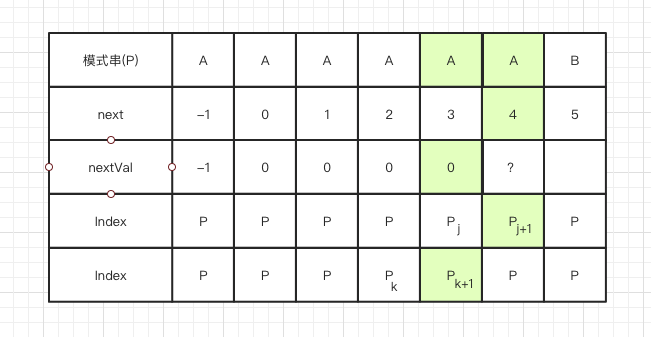
如何求nextVal数组呢？我们还是以上面的特殊情况为例，看两个状态：

此时我们已经求完了nextVal[j]的值，仔细观察状态图，发现：

• 根据求next数组的过程,next[j + 1] = k + 1

  • 若P_j+1 !== P_{next[j + 1]}，在P_{next[j + 1]}发生失配时，只要跳到P_j+1就有可能解决失配问题，则此时的 nextVal[j + 1] = next[j + 1]即可
  • 若P_j+1 === P_{next[j + 1]}，在P_{next[j + 1]}发生失配时，跳到P_j+1就并不能解决失配问题，则此时应该继续回溯nextVal的next[j + 1]的位置上（由于是迭代求法，此时nextVal[next[j + 1]]上的值一定是通过nextVal[next²[j + 1]]求得了），即 nextVal[j + 1] = nextVal[next[j + 1]]

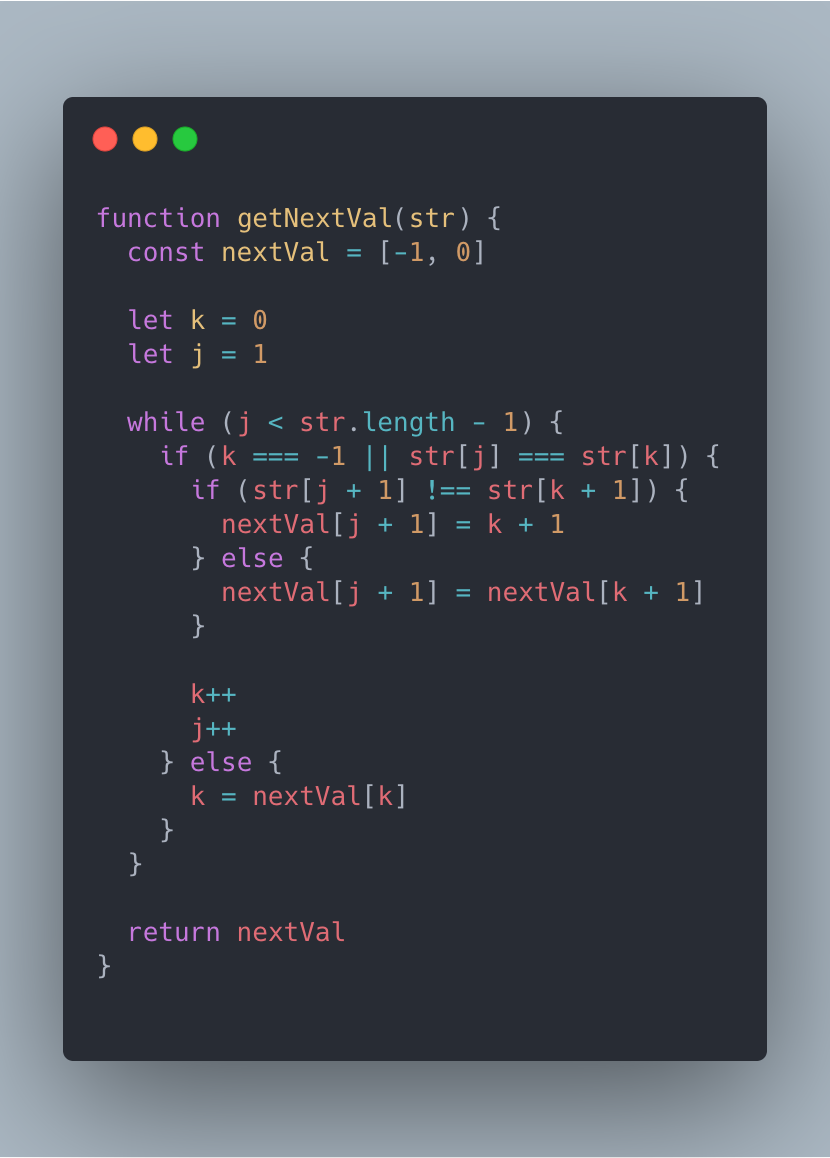
可以在 getNext() 的基础上得到以下代码：

next数组现在就已经是一个可有可无的工具人了，我们把去掉，得到下一版代码：

再进行以下优化得到最终代码：

总结

总的来说，KMP算法和BF算法的字符串匹配思路在大方向上是没有区别的，只是引入了一个next数组或nextVal数组来求得模式串中合适的位置。只要理解了这两个数组的求法，也就基本理解了KMP算法。

后记

“字符串匹配算法”是“重学数据结构与算法”系列笔记：

• 字符串匹配算法(一)——BF算法
• 字符串匹配算法(二)——KMP算法
• [字符串匹配算法(三)——BM算法]()
• [字符串匹配算法(四)——Sunday算法]()