【重学数据结构与算法(JS)】字符串匹配算法(三)——BM算法

前言

文章的一开头，还是要强调下字符串匹配的思路：

1. 将模式串和主串进行比较

   • 从前往后比较
   • 从后往前比较
2. 匹配时，比较主串和模式串的下一个位置

3. 失配时,

   • 在模式串中寻找一个合适的位置

     • 如果找到，从这个位置开始与主串当前失配位置进行比较
     • 如果未找到，从模式串的头部与主串失配位置的下一个位置进行比较
   • 在主串中找到一个合适的位置，重新与模式串进行比较

前面的 BF 和 KMP 算法，都是属于规规矩矩从前向后的操作，后者仅在寻找模式串的合适位置上进行了优化，而 BM 算法的操作就显得骚了很多，它的优化点在于：

1. 从后往前比较
2. 失配时，寻找的是主串中合适的位置

算法介绍与分析

关于算法的介绍和分析，网上有很多解释，这里推荐一下阮一峰的字符串匹配的Boyer-Moore算法，很清楚的讲解了整个优化的思路，可以先看完理解了再往下看，因为下面主要介绍一下坏字符规则和好后缀规则需要的数据结构的手工求法以及代码实现。

坏字符规则

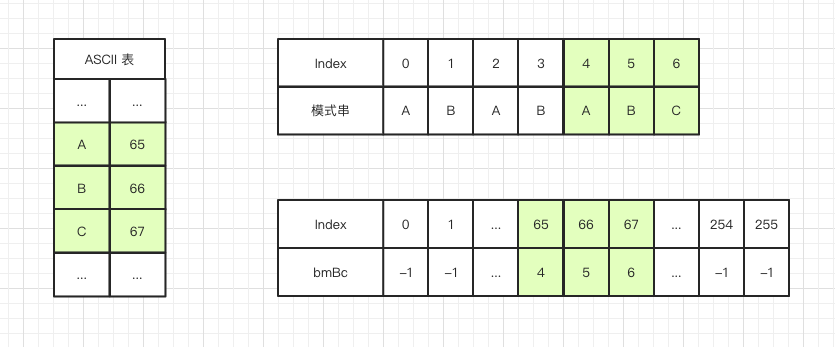
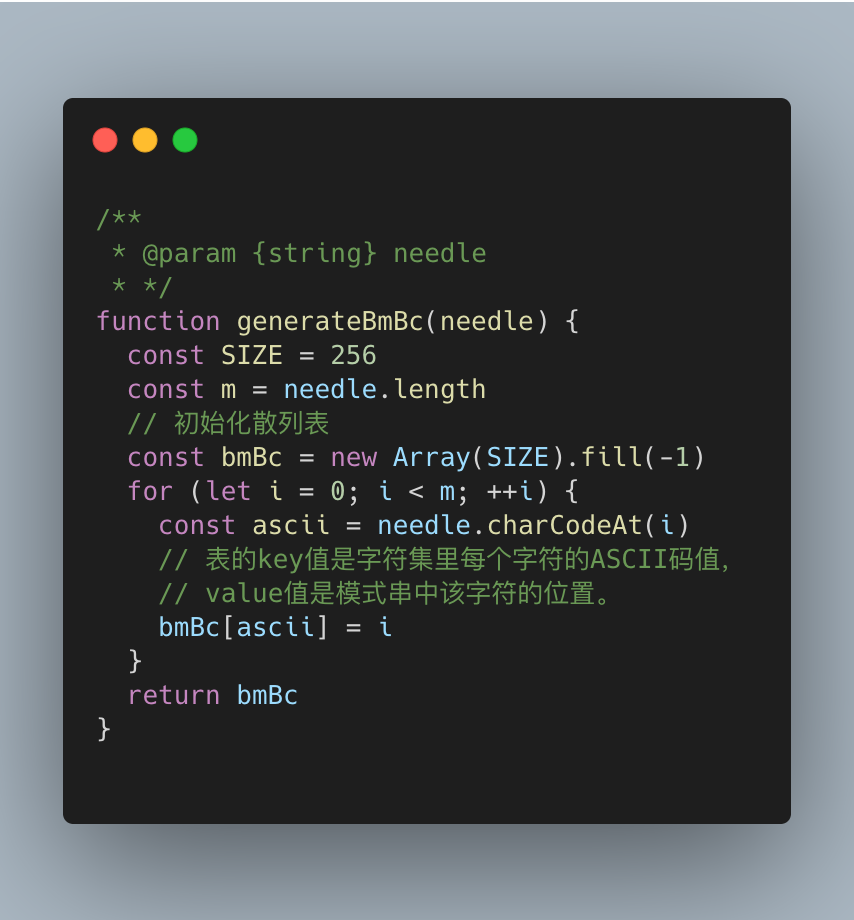
运用坏字符规则，在算法里主要体现在生成一张散列表，表的key值是字符集里每个字符的ASCII码值，value值是模式串中该字符的位置，举个栗子：

假设字符串的字符集不是很大，用长度为256的数组来存储，并且初值赋值为-1。数组的下标对应字符的 ASCII 码值，数组中存储这个字符在模式串中出现的位置。这里要特别说明一点，如果坏字符在模式串里多处出现，选择最靠后的那个，因为这样不会让模式串滑动过多，导致本来可能匹配的情况被滑动略过。

好后缀规则

好后缀规则体现在如何求出 suffix 和 prefix 两个数组以及移动规则。

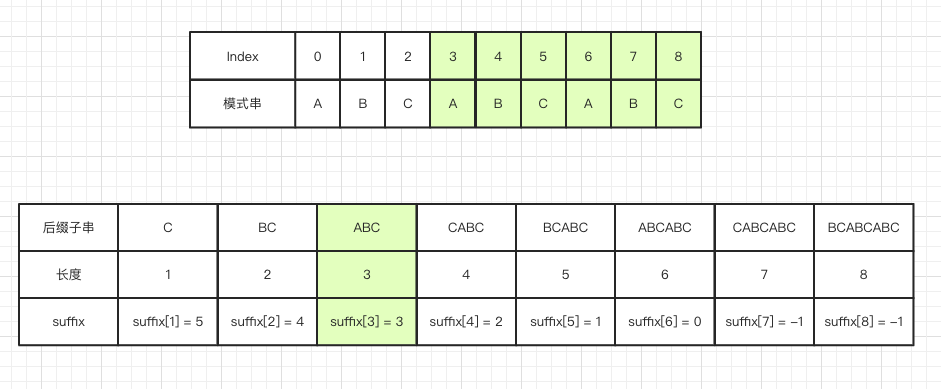
suffix 数组

key值表示的是后缀子串的长度，value值表示的是在模式串中跟好后缀 S 相匹配的最后一个子串 S^' 的首字母在模式串中的key值，如下图：

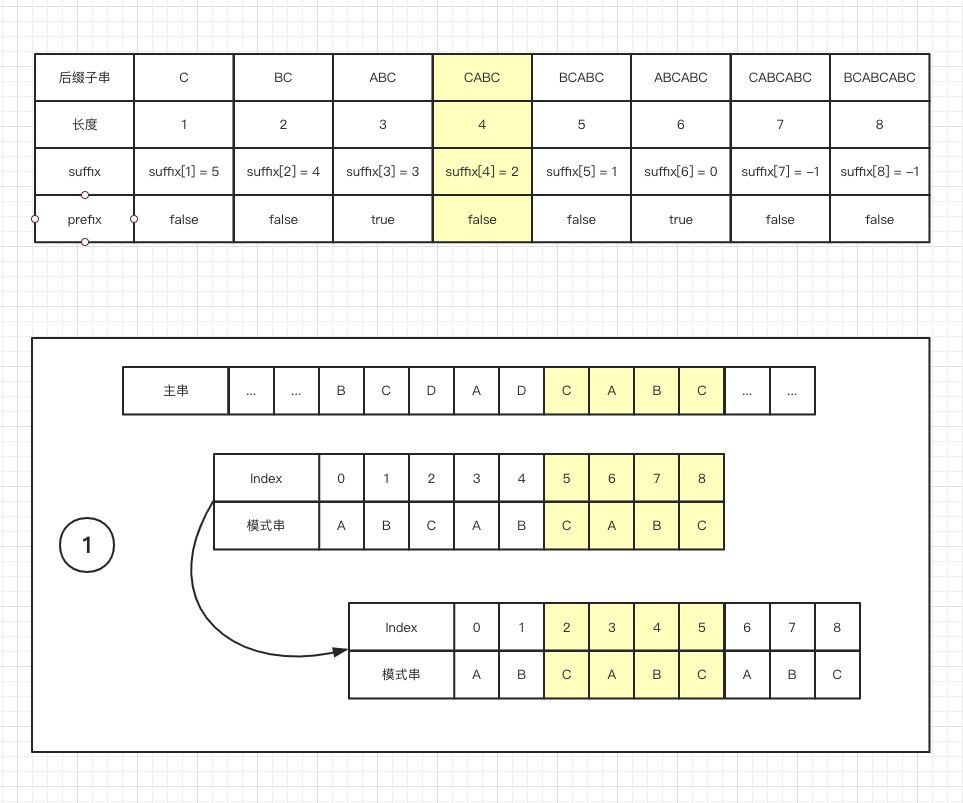
prefix 数组

同样的，key值表示的是后缀子串的长度，而value值表示的是模式串中，是否有和该长度下后缀子串相同的前缀子串，是的话为 true，否则为 false，如下图：

移动规则

移动规则总结如下：

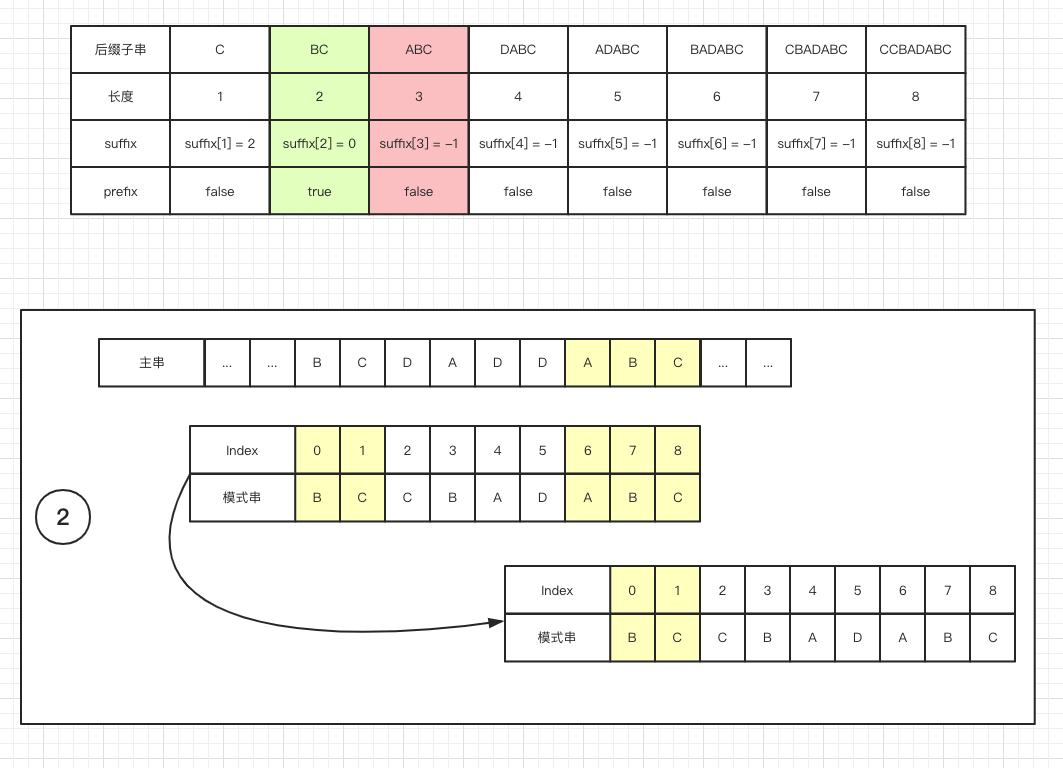
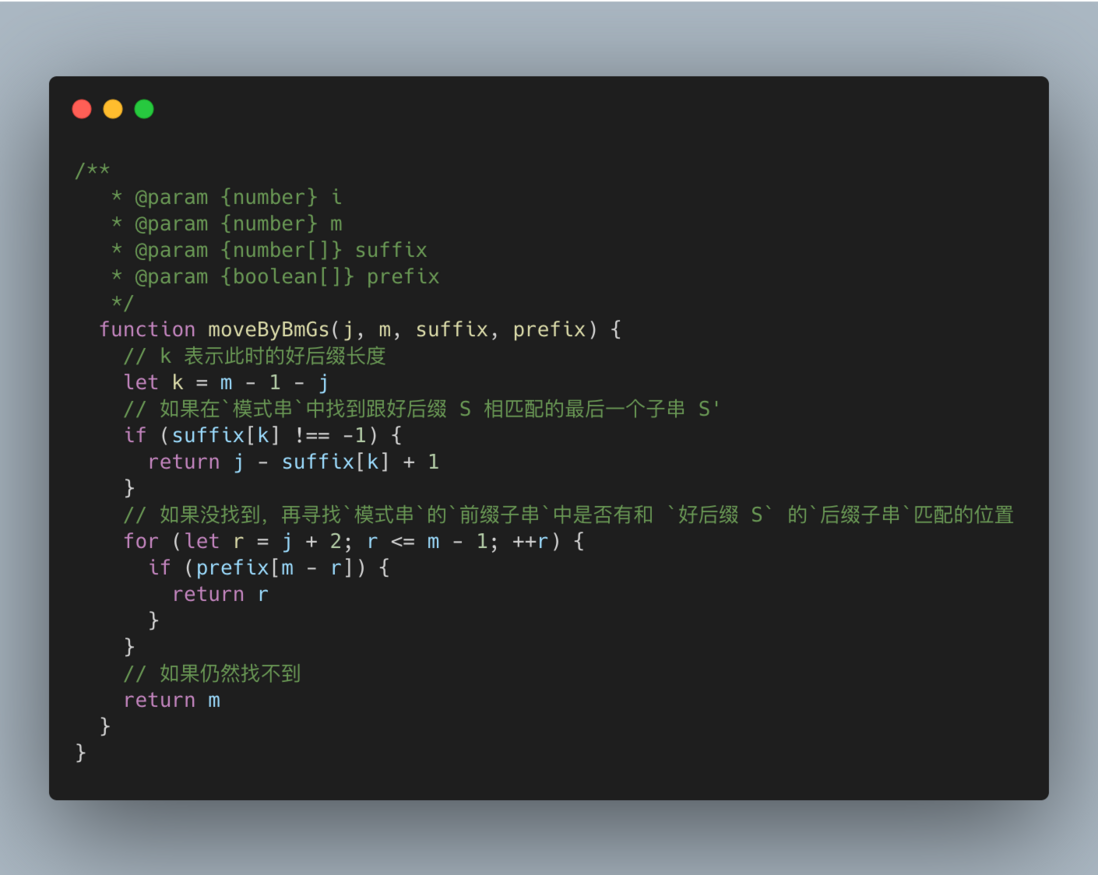
• 在模式串中寻找跟好后缀 S 相匹配的最后一个子串 S^'

  • 如果找到，将模式串移动到使得 S^' 和主串对齐的位置
  • 如果找不到，再寻找模式串的前缀子串中是否有和 好后缀 S 的后缀子串匹配的位置，滑动模式串以对齐。
  • 如果仍然找不到，则将模式串移动至主串与模式串末尾对齐的下一个位置

下图分别对应三种情况：

代码实现

整体逻辑框架

参考字符串匹配的思路

• 仍然需要进行主串和模式串的字符对比，所以需要两个指针 i ，j 分别指向主串和模式串，记录位置

• 需要一个循环来重复进行匹配操作，此时思考终止条件：

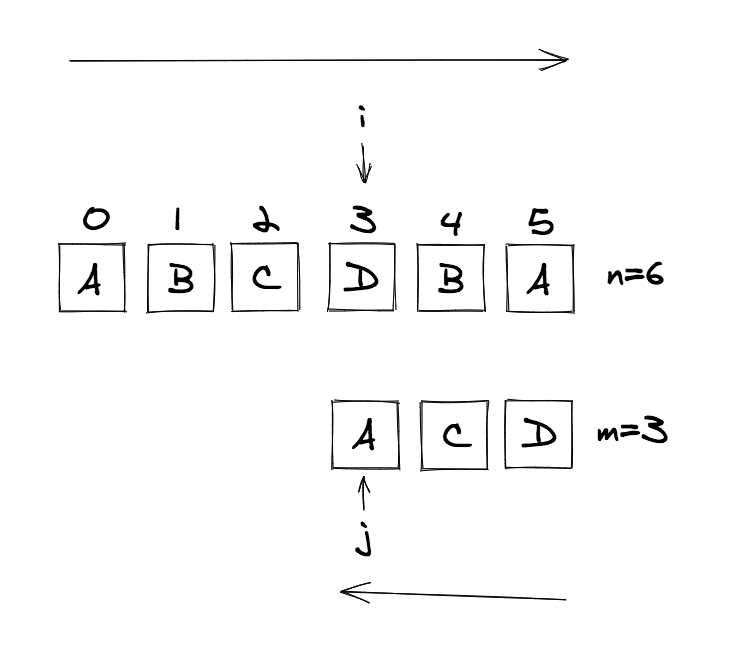
  • i 指向主串每次匹配的合适位置，从前往后扫描；j 指向模式串的尾部，从后往前扫描。考虑极端情况：主串和模式串对比完，仍然无法匹配。此时，i 的位置一定小于等于 主串长度 n 与模式串长度 m 的差值。具体可看下图。
• 每次模式串从后往前与主串进行匹配，这也需要一个内层循环来驱动指针j
• 如果匹配，只需要继续移动匹配位置即可
• 如果失配，分别根据坏字符规则和好后缀规则计算出 i 需要移动的位置，选择两个值当中最大的，重新计算 i 的值，重复进行匹配。

根据以上分析可以写出整个的逻辑框架代码：

框架写好后，接下来就是完善三个辅助函数即可

求坏字符散列表

这个就没有什么可以多说的了，只要参考上面分析的，一步一步写出代即可：

求好后缀记录数组 suffix 和 prefix

拿下标从 0 到 i 的子串（i 可以是 0 到 m-2）与整个模式串，求公共后缀子串。如果公共后缀子串的长度是 k，那就记录 suffix[k]=j（j 表示公共后缀子串的起始下标）。如果 j 等于 0，也就是说，公共后缀子串也是模式串的前缀子串，就记录 prefix[k]=true。可以自己动下手，模拟下代码的运行，尤其注意中k值的运用，很巧妙。

求好后缀移动步数

根据上面此步的算法分析，也可以写出：

总结

总的来说，BM算法另辟蹊径，通过从后往前的匹配的思路，加上坏字符规则和好后缀规则来优化移动的步数，从而提高算法的匹配效率。

后记

“字符串匹配算法”是“重学数据结构与算法”系列笔记：

• 字符串匹配算法(一)——BF算法
• 字符串匹配算法(二)——KMP算法
• 字符串匹配算法(三)——BM算法
• 字符串匹配算法(四)——Sunday算法