【详细笔记】JavaScript数字类型详解

头像
LazyDuke
    阅读 9 分钟
    2

    前言

    这是一篇偏综合性的总结，根据笔者的 routine 整理好的，并对代码进行了改进。以下内容出处均已在 参考资料 中列出，如有侵权，联系笔者删除。

    思维导图

    前置知识

    本质原因

    计算机是二进制的，无法直接表示正负数，另外在计算机内部直接实现减法，也会影响计算机效率，所以人们希望要找到一种既能使用二进制表示10进制正负数的编码格式，同时这种编码格式又能满足将减法转换成加法进行运算。

    原码、反码和补码

    原码

    image.png

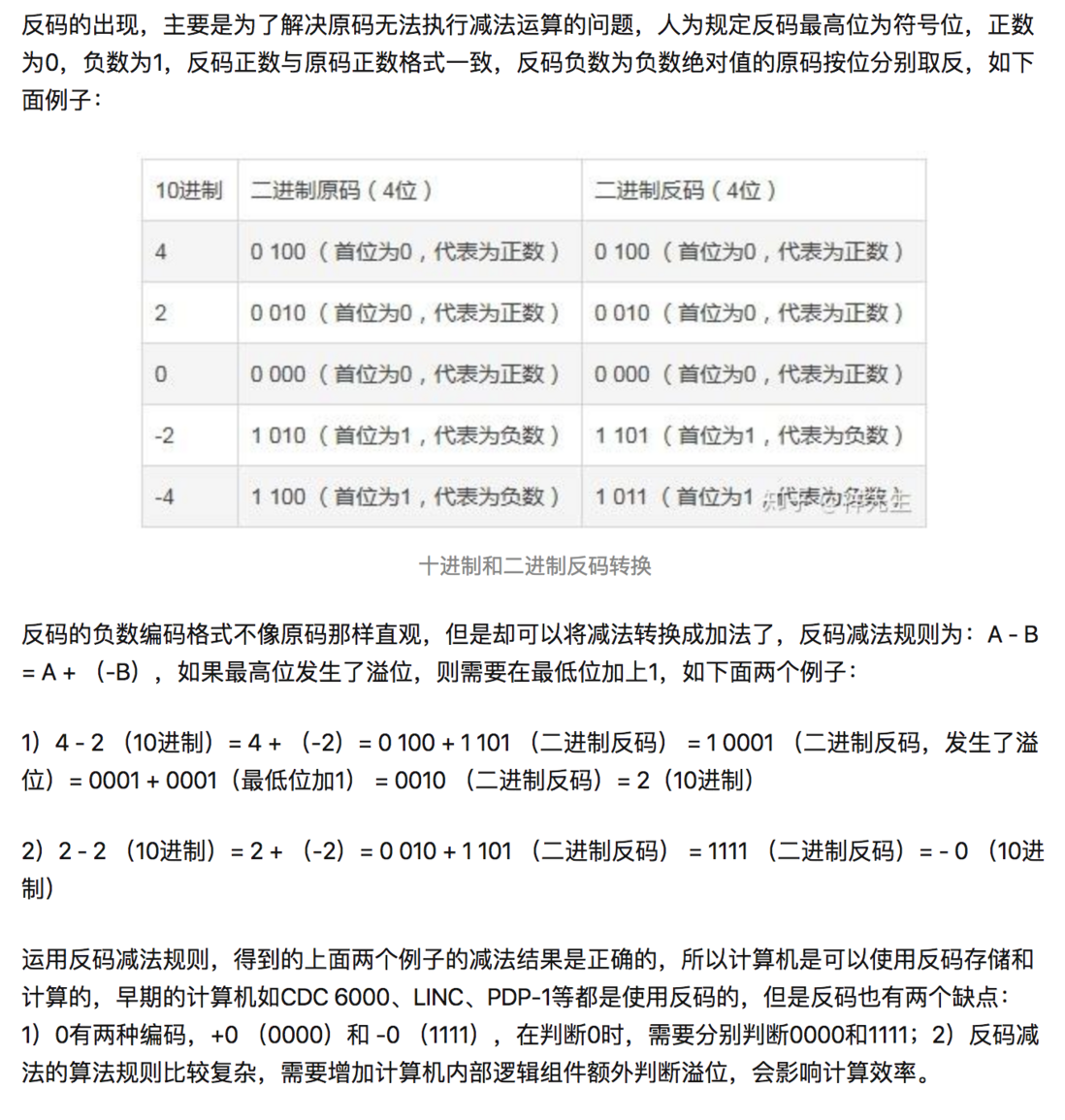
    反码

    image.png

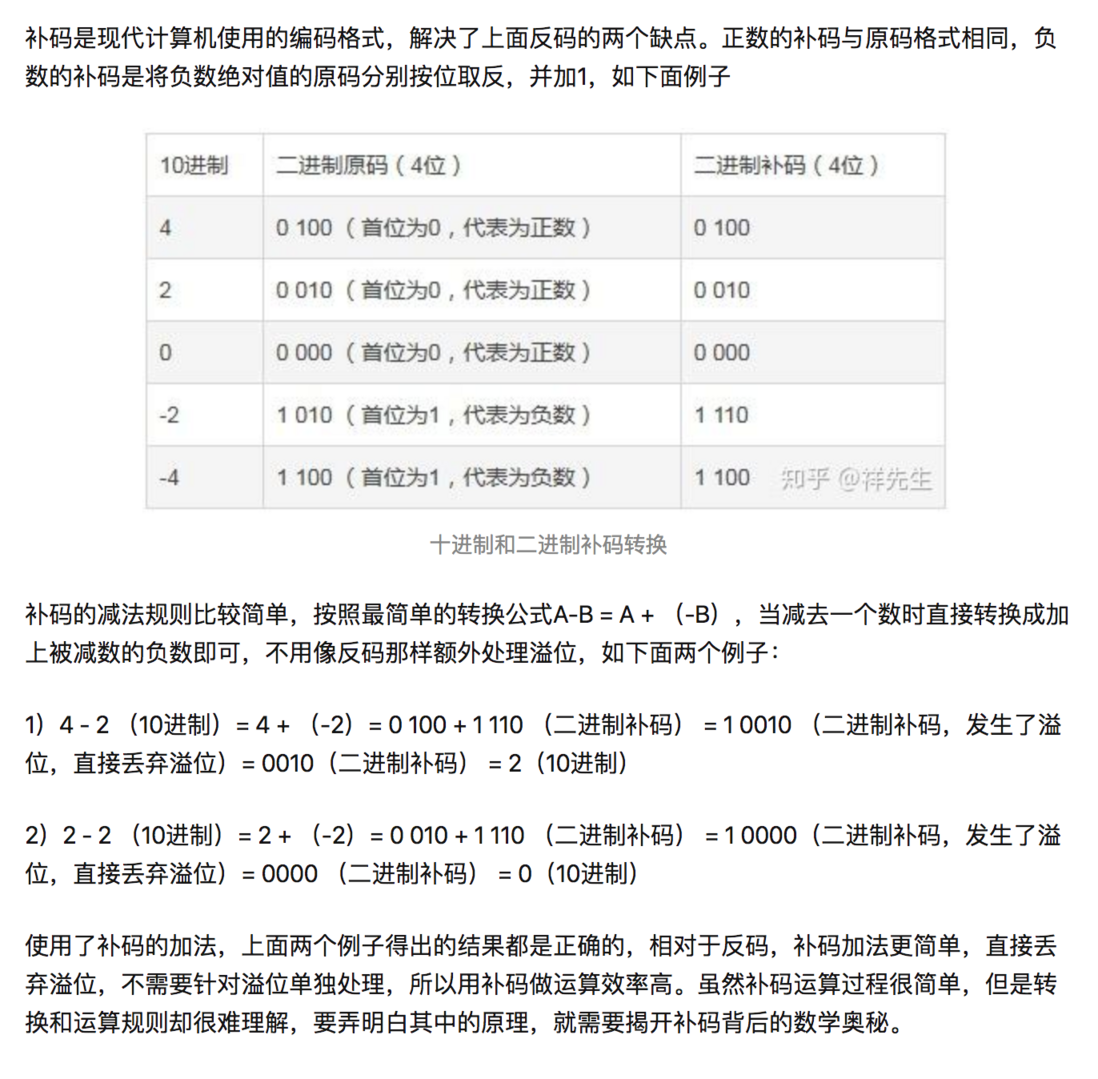
    补码

    image.png

    总结

    要想弄清楚补码，必须要弄清楚补码要解决的问题，计算机是二进制的，无法直接表示正负数，另外在计算机内部直接实现减法，也会影响计算机效率，所以人们希望要找到一种既能使用二进制表示10进制正负数的编码格式，同时这种编码格式又能满足将减法转换成加法进行运算，同时满足这两个条件有反码和补码，但由于反码中的0有两个编码格式，另外反码加法运算也比较复杂，慢慢地反码被淘汰了。补码刚好解决了反码的两个缺点，所以补码成了现代计算机的通用编码。

    IEEE 754标准

    背景

    随着技术的更新，在1978年的时候，Intel公司推出了首枚16bit微处理器(CPU)8086。这台x86的老祖宗虽然自身无法处理小数的运算，但是在编译器层面可以通过用整数指令模拟出小数的运算，不过这种运算的方式效率是非常低的。


    为了解决这类问题，1980年Intel公司推出了首款x87浮点协处理器运算单元(FPU)8087，通过主板上额外的协处理器插槽，安装后不仅可以解决小数的运算问题，并且对于不同的应用，性能提升了20%~500%。


    对于计算机发展来说，8087是款非常棒的FPU，但是它的意义真正体现在这款FPU的设计师之一的William Kahan教授设计了IEEE-754标准的雏形，而正是因为这套标准，我们计算机才能精准的处理小数。


    1985年时，IEEE推出了IEEE 754-1985标准，随着大佬们的努力，IEEE还推出了目前的版本——IEEE 754-2008。


    而我们使用的高级语言中浮点数的运算，如C、C++、JavaScript、Java都是基于这个标准而定。

    概念

    image.png
    image.png
    或
    image.png
    也叫
    image.png

    概念

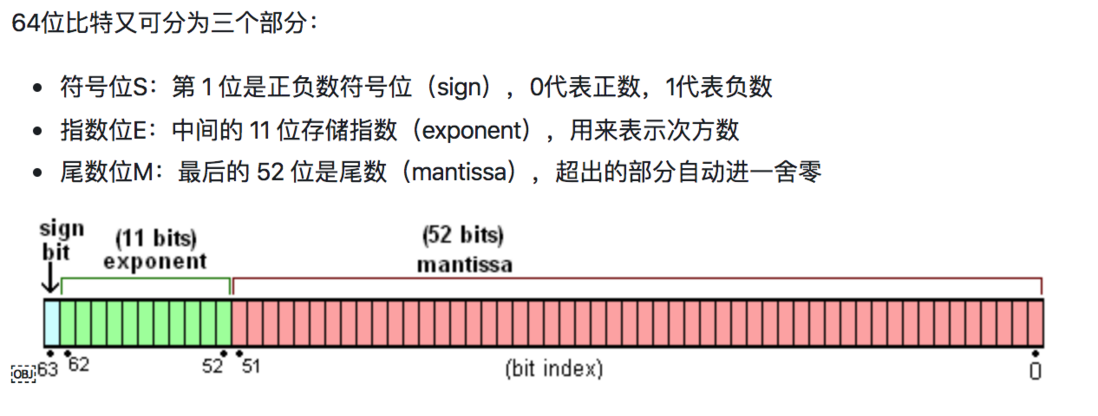
    JavaScript的数字类型的本质就是一个基于 IEEE 754 标准的双精度 64 位的浮点数。

    小数运算（为什么0.2 + 0.1 !== 0.3？）

    概述

    1. 0.1 和 0.2 按照 IEEE 754 存储后都有精度损失
    2. 运算后进行规格化时的舍入操作也有精度损失

    **

    详解

    关于浮点数的运算，一般由以下五个步骤完成：对阶、尾数运算、规格化、舍入处理、溢出判断。
    image.png
    将它转换为10进制数就得到 0.30000000000000004440892098500626
    因为两次存储时的精度丢失加上一次运算时的精度丢失，最终导致了 0.1 + 0.2 !== 0.3

    解决方案

    number-precision
    全面总结 JS 中浮点数运算问题 - 掘金

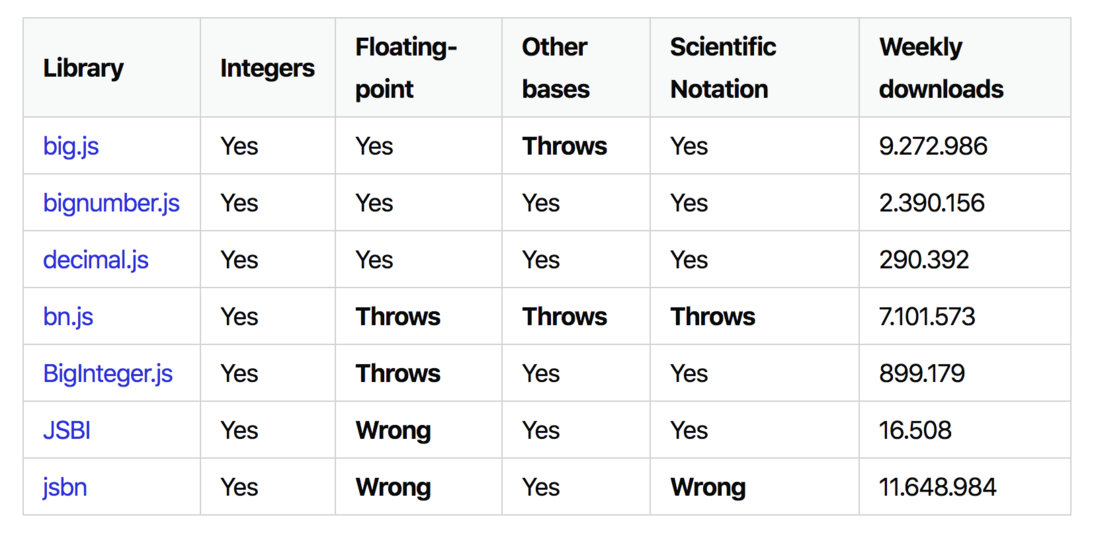
    大数运算如何处理？

    现成方案

    1.bignumber.js
    2.true-json-bigint.js
    3.BigInt - JavaScript | MDN
    image.png

    大数运算

    核心思想

    既然数字类型会有精度问题，那就统统转用字符串来处理。

    大数相加


    普通版本

    /**
 * @param {string} a
 * @param {string} b
 * @return {number}
 */
function add(a, b) {
  // 首先检查传来的大数是否是字符串类型，如果传Number类型的大数，在传入的时候已经丢失精度了，
  // 就如 如果传入11111111111111111，处理的时候已经是丢失精度的11111111111111112了，则需要传入
  // 字符串类型的数字 '11111111111111111'
  const checkNum = num => typeof num === "string" && !isNaN(Number(num))
  // 格式化数字
  const formatNum = num => (isNaN(+num) ? 0 : +num)

  if (!checkNum(a) || !checkNum(b)) {
    throw new TypeError("Big Number Type Error")
  }
  const result = []

  a = a.split("").reverse()
  b = b.split("").reverse()
  const length = Math.max(a.length, b.length)

  let carry = 0
  
  // 以较长的数字为基准进行从前往后逐个加和，为避免两个数相加最高位进位后，导
  // 致结果长度大于两个数字中的长度，for循环加和长度为最长数字长度加一
  for (let i = 0; i <= length; i++) {
    const tempResult = formatNum(a[i]) + formatNum(b[i]) + carry
    result[i] = tempResult % 10
    
    // 当加和的数字大于10的情况下，进行进位操作，将要进位的数字赋值给temp，在下一轮使用
    carry = Math.trunc(tempResult / 10)
  }
  
  // 计算完成，反转回来
  result.reverse()
  
  // 将数组for中多加的一位进行处理，如果最高位没有进位则结果第一个数位0，
  // 结果第一个数位1，则发生了进位。 如99+3，最大数字长度位2,结果数长度位3
  // 此时结果的第一位为1，发生了进位，第一位保留，如果是2+94，第一位为0，则不保留第一位
  return result.join('').replace(/^0+/, "")
}


    奇技淫巧版

    /**
 * @param {string} a
 * @param {string} b
 * @return {number}
 */
function add(a, b) {
  const checkNum = num => typeof num === "string" && !isNaN(Number(num))

  if (!checkNum(a) || !checkNum(b)) {
    throw new TypeError("Big Number Type Error")
  }

  let result = ""

  let c = 0
  a = a.split("")
  b = b.split("")

  while (a.length || b.length || c) {
    
    // ~取反操作符，~0 === -1, ~~0 === 0, ~~null === 0, ~~undefined === 0, ~~'0' === 0
        // 用+也能实现字符转成数字，不过~~能处理null的情况
    c = ~~a.pop() + ~~b.pop() + c
    result += c % 10
    
    // c>0会返回一个布尔值，布尔值转换成数字的时候true为1，false为0
    c = c > 9
  }

  return result.replace(/^0+/, "")
}


    优化版

    /**
 * @param {string} a
 * @param {string} b
 * @return {number}
 */
function add(a, b) {
  const checkNum = num => typeof num === "string" && !isNaN(Number(num))

  if (!checkNum(a) || !checkNum(b)) {
    throw new TypeError("Big Number Type Error")
  }
  
  // 主要思想是分开一段段加，这样既能保证精度且不溢出，也能提高速度
    // 如果索引超范围，或者长度小于1那么返回空字符串

  const MAX_PERCISION = Number.MAX_SAFE_INTEGER.toString().length - 1
  const arr = []

  while (a.length || b.length) {
    arr.push(
      parseInt(a.substring(a.length - MAX_PERCISION) || 0, 10) +
      parseInt(b.substring(b.length - MAX_PERCISION) || 0, 10)
    )
    a = a.substring(0, a.length - MAX_PERCISION)
    b = b.substring(0, b.length - MAX_PERCISION)
  }

  let carry = 0
  let result = ""

  while (arr.length) {
    const temp = (arr.shift() + carry).toString()
    result = temp.substring(temp.length - MAX_PERCISION) + result
    carry = parseInt(
      temp.substring(0, temp.length - MAX_PERCISION) || 0,
      10
    )
  }

  return result
}

// 简化 =>

/**
 * @param {string} a
 * @param {string} b
 * @return {number}
 */
function add(a, b) {
  const checkNum = num => typeof num === "string" && !isNaN(Number(num))

  if (!checkNum(a) || !checkNum(b)) {
    throw new TypeError("Big Number Type Error")
  }

  const MAX_PERCISION = Number.MAX_SAFE_INTEGER.toString().length - 1

  let result = ""
  let carry = 0

  while (a.length || b.length) {
    const temp = (
      parseInt(a.substring(a.length - MAX_PERCISION) || 0, 10) +
      parseInt(b.substring(b.length - MAX_PERCISION) || 0, 10) +
      carry
    ).toString()
    result = temp.substring(temp.length - MAX_PERCISION) + result
    carry = parseInt(
      temp.substring(0, temp.length - MAX_PERCISION) || 0,
      10
    )

    a = a.substring(0, a.length - MAX_PERCISION)
    b = b.substring(0, b.length - MAX_PERCISION)
  }

  return result
}

    大数相减


    奇技淫巧版

    /**
 * @param {string} a
 * @param {string} b
 * @return {number}
 */
function minus(a, b) {
  const checkNum = num => typeof num === "string" && !isNaN(Number(num))

  if (!checkNum(a) || !checkNum(b)) {
    throw new TypeError("Big Number Type Error")
  }

  while (a.length < b.length) {
    a = "0" + a
  }
  while (b.length < a.length) {
    b = "0" + b
  }

  let result = ""
  let borrow = false

  a = a.split("")
  b = b.split("")

  while (a.length) {
    const minuend = ~~a.pop()
    const subtrahend = ~~b.pop() + borrow

    if (minuend >= subtrahend) {
      borrow = minuend - subtrahend
      result = borrow + result
      borrow = false
    } else {
      borrow = minuend + 10 - subtrahend
      result = borrow + result
      borrow = true
    }
    //判断最高位有无借位，若有借位，则说明结果为负数
    if (a.length === 0 && borrow) {
      result = "-" + result
    }
  }

  result = result.replace(/^0+/, "")

  //判断最后的结果是否为0
  if (result === "") {
    result = 0
  }
  return result
}

    大数相乘

    目前大数乘法算法主要有以下几种思路：

    1. 模拟小学乘法：最简单的乘法竖式手算的累加型；
    2. 分治乘法：最简单的是Karatsuba乘法，一般化以后有Toom-Cook乘法；
    3. 快速傅里叶变换FFT：（为了避免精度问题，可以改用快速数论变换FNTT），时间复杂度O(N lgN lglgN)。具体可参照Schönhage–Strassen algorithm；
    4. 中国剩余定理：把每个数分解到一些互素的模上，然后每个同余方程对应乘起来就行；
    5. Furer’s algorithm：在渐进意义上FNTT还快的算法。不过好像不太实用，本文就不作介绍了。大家可以参考维基百科Fürer’s algorithm


    模拟小学乘法版

    /**
 * @param {string} a
 * @param {string} b
 * @return {string}
 */
function multiply(a, b) {
  const cn = a.length + b.length
  const c = new Array(cn).fill(0)
  /****
         * 两两相乘，并放进不同的格子里，如果里面有东西，则相加
         * 0
         *   8
         *     10
         *     4
         *       5
         */
  for (let i = 0; i < a.length; i++) {
    for (let j = 0; j < b.length; j++) {
      c[i + j + 1] += Number(a[i]) * Number(b[j])
    }
  }
  // 处理进位
  for (let i = cn - 1; i >= 0; i--) {
    const carry = Math.trunc(c[i] / 10)
    if (carry) {
      c[i - 1] += carry
    }
    c[i] = c[i] % 10
  }
  while (c[0] === 0) {
    c.shift()
  }
  //处理最前面的零
  return c.join("") || "0"
}


    利用下标取巧版

    /**
 * @param {string} a
 * @param {string} b
 * @return {string}
 */
function multiply(num1, num2) {
    const checkNum = num => typeof num === "string" && !isNaN(Number(num))

  if (!checkNum(a) || !checkNum(b)) {
    throw new TypeError("Big Number Type Error")
  }
 
  let len1 = a.length,
      len2 = b.length
  let ans = []

  //这里倒过来遍历很妙,不需要处理进位了
  for (let i = len1 - 1; i >= 0; i--) {
    for (let j = len2 - 1; j >= 0; j--) {
      let index1 = i + j,
          index2 = i + j + 1
      let mul = a[i] * b[j] + (ans[index2] || 0)
      ans[index1] = Math.floor(mul / 10) + (ans[index1] || 0)
      ans[index2] = mul % 10
    }
  }

  //去掉前置0
  let result = ans.join("").replace(/^0+/, "")

  //不要转成数字判断，否则可能会超精度！
  return !result ? "0" : result
}

    大数相除

    /**
 * @param {string} a
 * @param {string} b
 * @return {string}
 */
function divide(a, b) {
  const checkNum = num => typeof num === "string" && !isNaN(Number(num))

  if (!checkNum(a) || !checkNum(b)) {
    throw new TypeError("Big Number Type Error")
  }
  
  const alen = a.length
  const blen = b.length
  let quotient = 0
  let remainder = 0
  const result = []
  let temp = 0
  for (let i = 0; i < alen; i++) {
    temp = remainder * 10 + parseInt(a[i])
    if (temp < b) {
      remainder = temp
      result.push(0)
    } else {
      quotient = parseInt(temp / b)
      remainder = temp % b
      result.push(quotient)
    }
  }
  return [result.join("").replace(/\b(0+)/gi, ""), remainder] //结果返回[商，余数]
}

    大数阶乘

    function fact(num) {
  let result = 1
  for(let i=1; i<=num; i++){
    result = result * i
  }
  return result
}

// => 

function fact(num) {
  const checkNum = num => typeof num === "string" && !isNaN(Number(num))

  if (!checkNum(num)) {
    throw new TypeError("Big Number Type Error")
  }
  
  let result = "1"
  for (let i = "1"; lte(i, num); i = add(i, "1")) {
    result = multiply(result, i)
  }
  return result
}

function lte(num1, num2) {
  if (num1.length < num2.length) {
    return true
  } else if (num1.length === num2.length) {
    return num1 <= num2
  } else {
    return false
  }
}

    参考资料

    1. 原码、反码、补码的产生、应用以及优缺点有哪些？
    2. 原码, 反码, 补码 详解 - ziqiu.zhang - 博客园
    3. IEEE-754标准与浮点数运算_C/C++_马骏超的博客-CSDN博客
    4. JavaScript 深入之浮点数精度 - 掘金
    5. 为什么不要在 JavaScript 中使用位操作符？ | 咀嚼之味
    6. [[每日一题] JavaScript面试之“大数相加”运算 - 云+社区 - 腾讯云](https://cloud.tencent.com/dev...
    7. A comparison of BigNumber libraries in JavaScript
    8. 谈谈JS中的大数运算 | 前端脚印
    9. 有趣的大数运算
    10. JavaScript实现大整数减法_JavaScript_xiaoxiaoyoumeng的博客-CSDN博客
    11. js实现大数相乘 - 个人文章 - SegmentFault 思否
    12. [[leetcode] 大数乘法](https://zhuanlan.zhihu.com/p/...
    13. 【算法】大数乘法问题及其高效算法 | iTimeTraveler
    javascript
    LazyDuke
    113 声望5 粉丝
    « 上一篇
    【重学数据结构与算法(JS)】字符串匹配算法(四)——Sunday算法
    下一篇 »
    关于用设计模式刷 LeetCode 这件事

    引用和评论

    推荐阅读
    头像
    关于用设计模式刷 LeetCode 这件事

    LazyDuke赞 3阅读 1.4k

    头像
    腾讯新闻中心首页改版啦

    小蚊酱赞 11阅读 9.4k评论 7

    头像
    前端如何入门 Go 语言

    robin赞 26阅读 7.7k评论 8

    头像
    100个React最佳实践小技巧

    夕水赞 17阅读 2.6k评论 4

    头像
    前端开发工具

    寒青赞 15阅读 4.7k

    头像
    开发插件集合

    寒青赞 12阅读 3.1k

    头像
    JS校验身份证号

    寒青赞 10阅读 4.3k评论 2

    0 条评论
    得票最新