【重学数据结构与算法(JS)】字符串匹配算法(四)——Sunday算法

前言

惯例，最重要的匹配思路还是要贴一遍：

1. 将模式串和主串进行比较

   • 从前往后比较
   • 从后往前比较
2. 匹配时，比较主串和模式串的下一个位置

3. 失配时,

   • 在模式串中寻找一个合适的位置

     • 如果找到，从这个位置开始与主串当前失配位置进行比较
     • 如果未找到，从模式串的头部与主串失配位置的下一个位置进行比较
   • 在主串中找到一个合适的位置，重新与模式串进行比较

Sunday算法也许是三种里面最好理解也最好写的一种了，它的思路也是在于失配时如何跳过尽可能多的字符，具体的说，主要是优化了第3步，失配时，在主串中找到一个合适的位置，重新与模式串进行比较。

算法介绍与分析

• 从主串和模式串的首位开始比较，记

  • 主串 S
  • 模式串 P
  • 主串长度 slen
  • 模式串长度 plen
  • 主串位置指针 i
  • 模式串位置指针 j
  • 每次重新匹配时，模式串尾部对应主串位置的下一位 m

• 判断 S[i] 与 P[j] 是否相等

  • 如果相等

    • 判断 j 与 plen-1 是否相等，如果相等则表示 表示模式串匹配完成，直接返回 i - j 即可
    • 如果不相等，则继续比较下一位，即 i++;j++;

  • 如果不相等

    • 查看 S[m] 字符是否存在于 P 中，如果存在，将 P 移至两字符对应的位置上
    • 如果不存在，则移至 S[m] 的后一位
• 如果移动后， m > slen ，说明 S 已经遍历一遍，仍然没有找到目标，模式串 匹配失败。

栗子

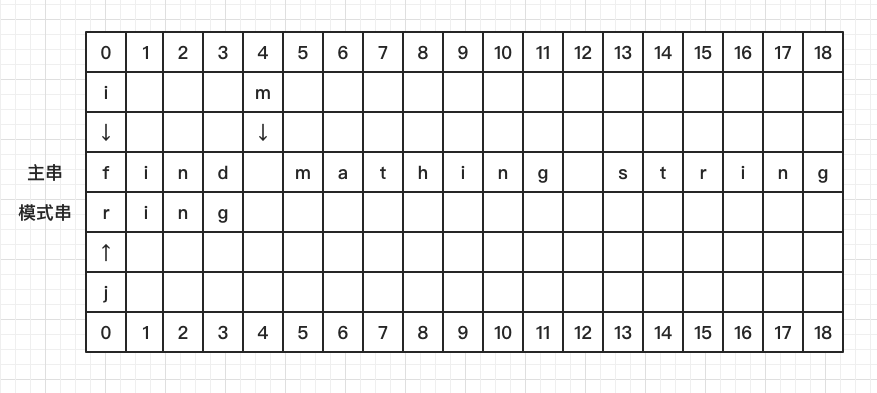
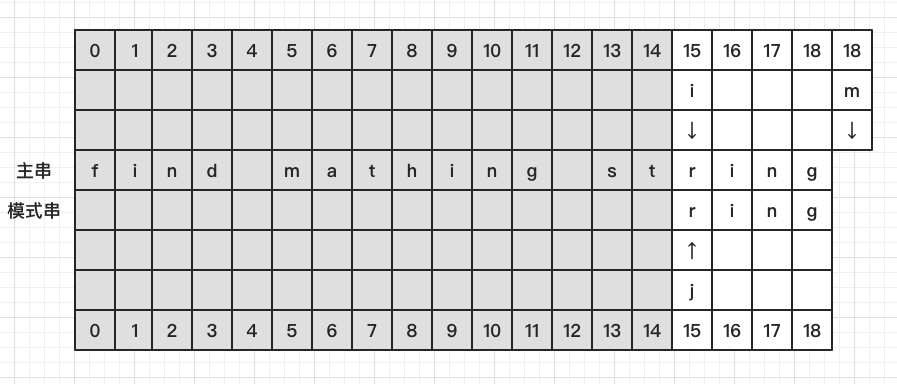
初始状态，i = 0, j = 0, m = 4

---

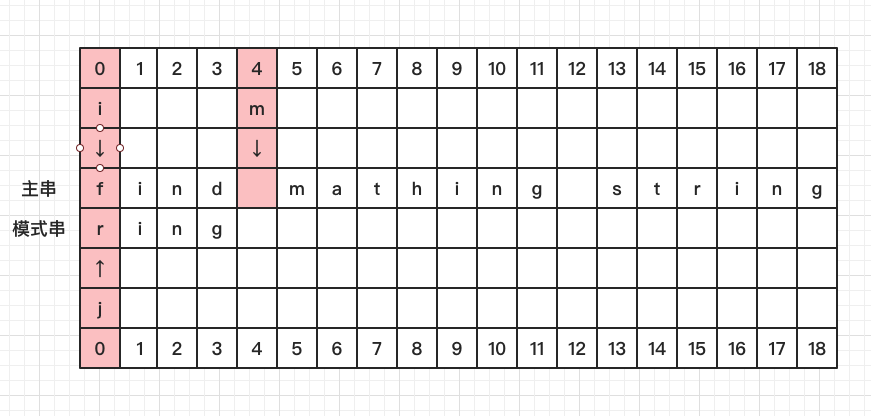
比较 S[0] 和 P[0]，发现不相等，看 S[4] 处发现并没有在 P 中出现

---

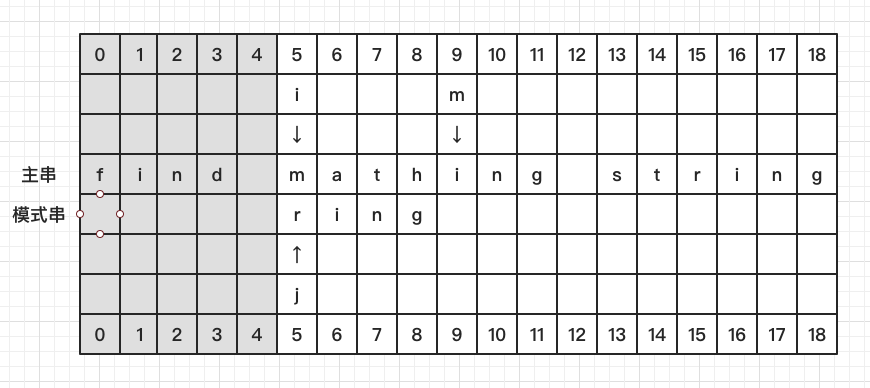
直接将 P 移至 S[4] 的后一位，此时 i = 5, j = 0, m = 9

---

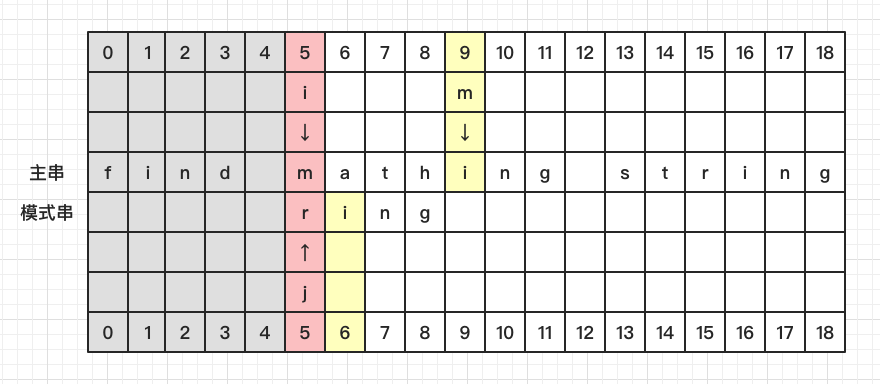
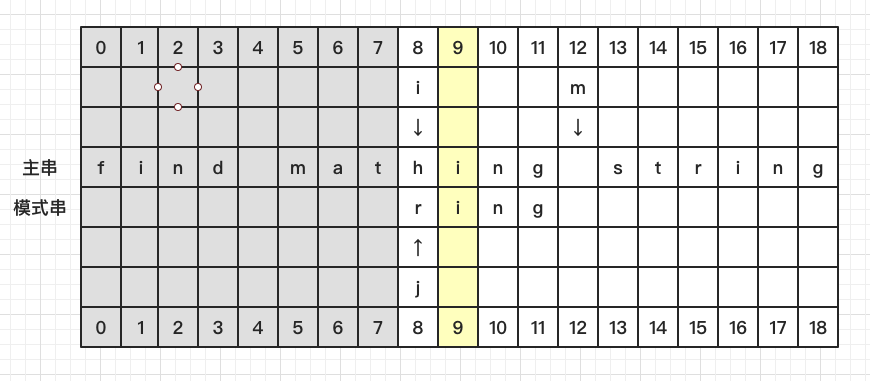
比较 S[5] 和 P[0]，发现不相等，看 S[9] 处发现有在 P 中出现

---

将 P 中的 i 与 S 中的 i 对齐，此时 i = 8, j = 0, m = 12

---

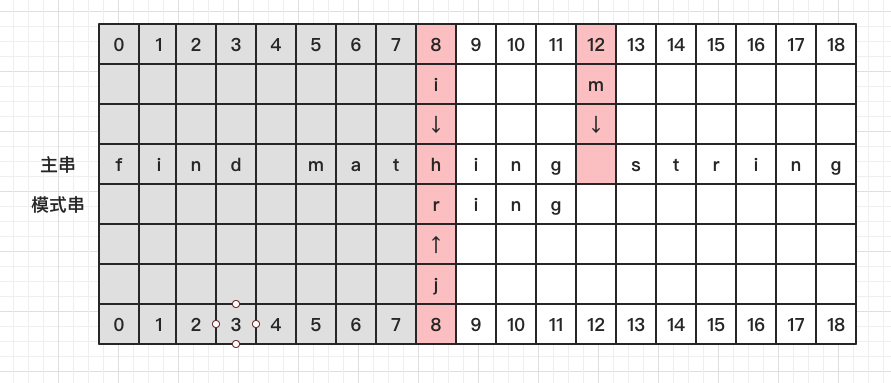
比较 S[8] 和 P[0]，发现不相等，看 S[12] 处发现并没有在 P 中出现

---

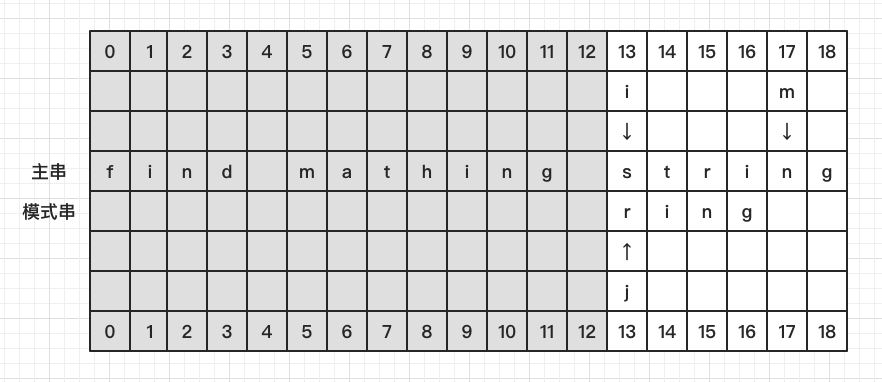
直接将 P 移至 S[12] 的后一位，此时 i = 13, j = 0, m = 17

---

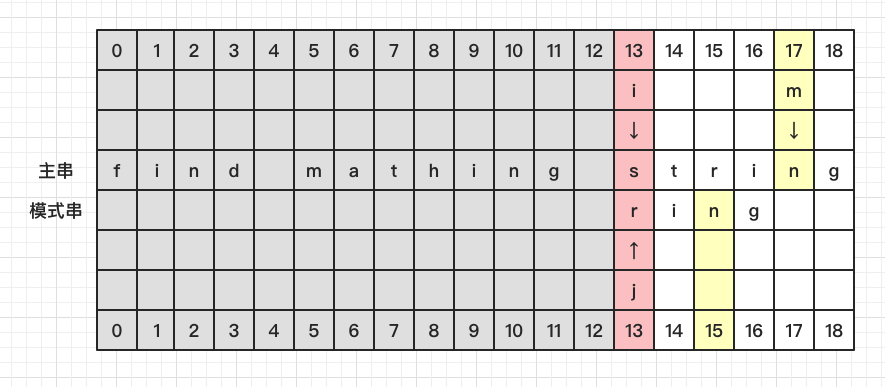
比较 S[13] 和 P[0]，发现不相等，看 S[17] 处发现有在 P 中出现

---

将 P 中的 n 与 S 中的 n 对齐，此时 i = 15, j = 0, m = 18

---

继续匹配，直到 j === plen - 1 = 3，则匹配成功，得到结果 i - j = 18 - 3 = 15

代码实现

极端情况的排除

整体逻辑框架

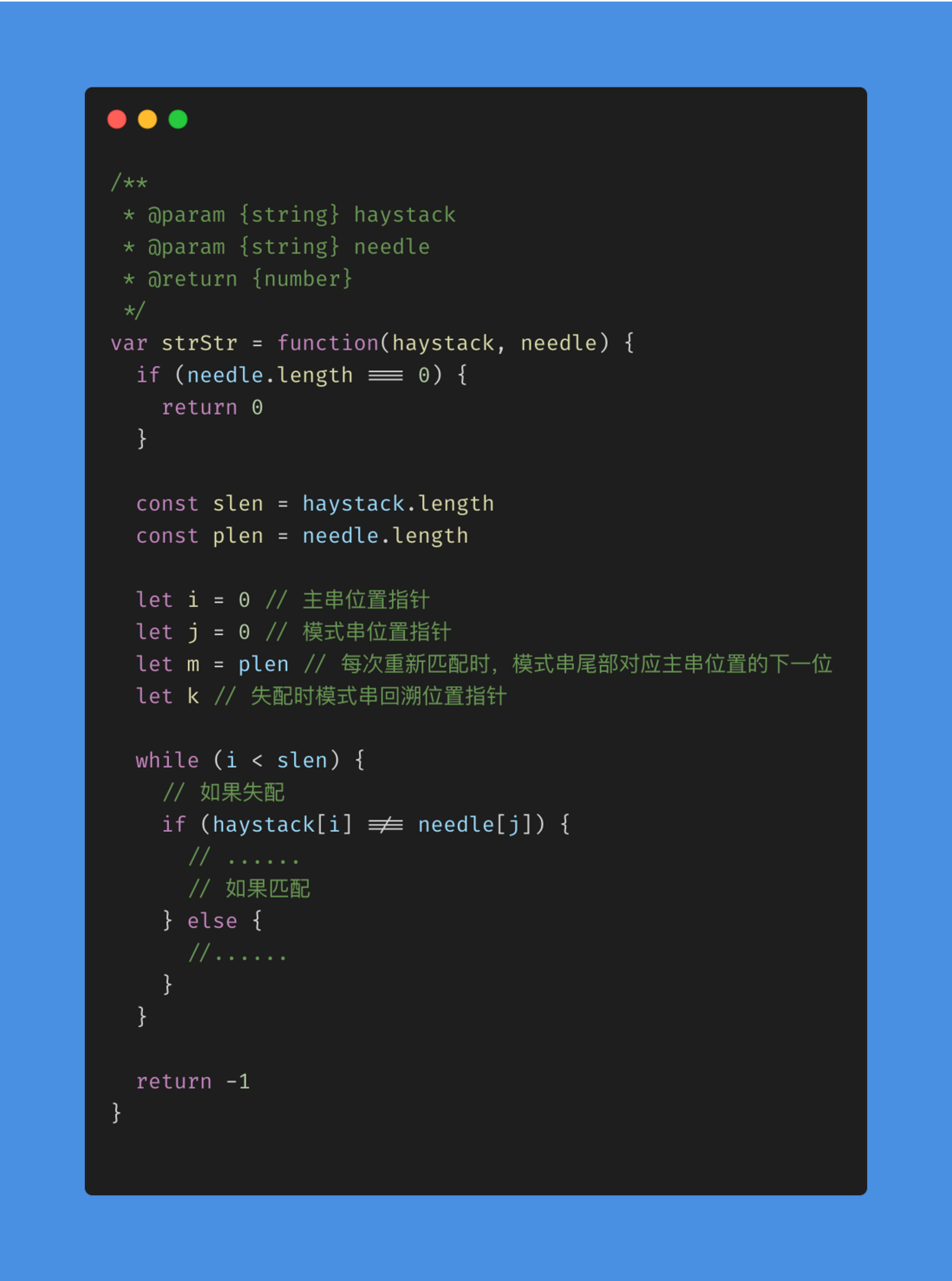
• 首先，肯定有一个循环，先找到终结条件，和 BF算法 一样，查找顺序也是从前往后，可以很快知道，i < slen 就是终结的条件
• 其次，就是要对匹配和失配进行不同的处理

由此，我们就可以写出整体的框架：

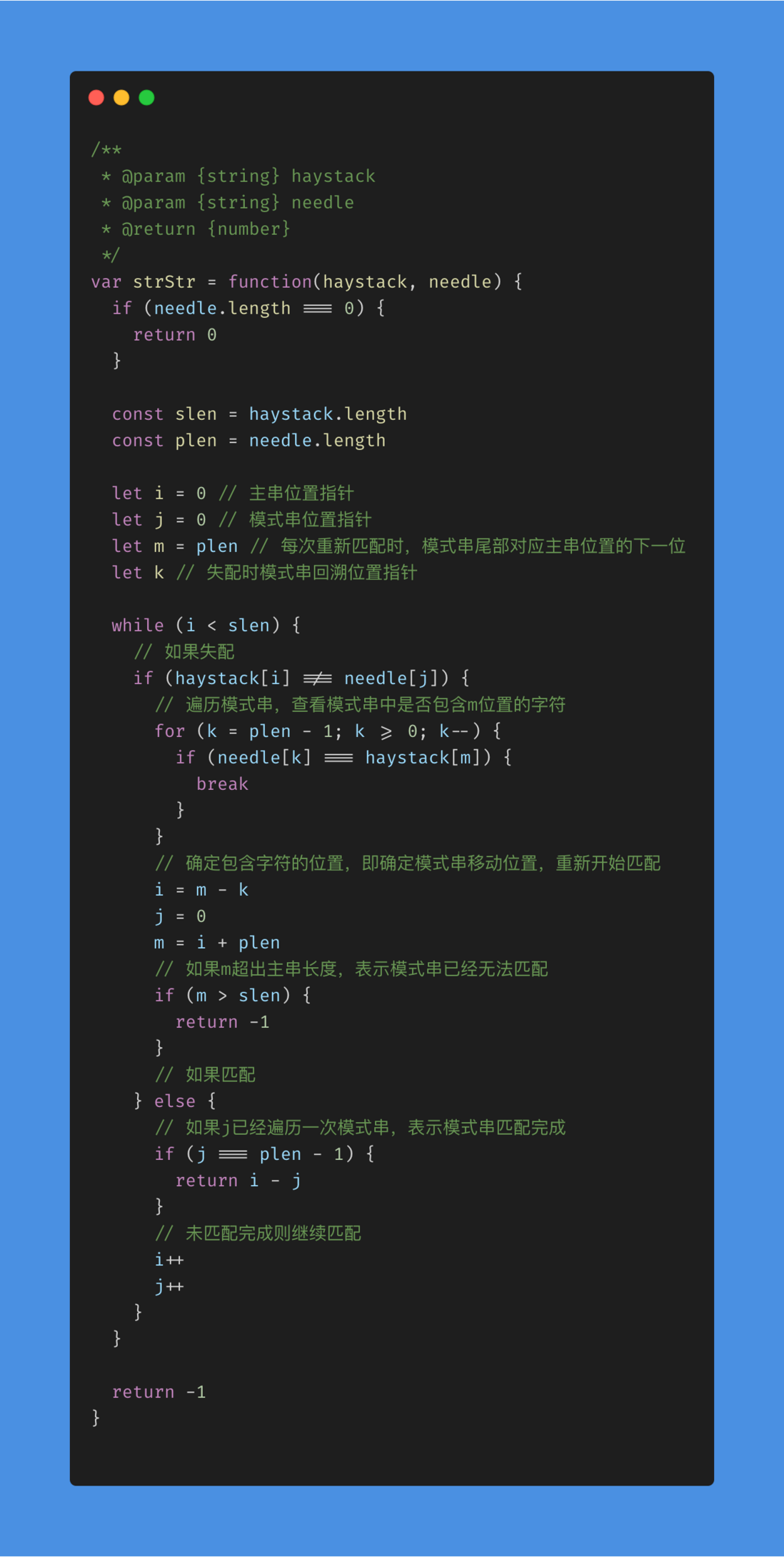
细节的完善

总结

Sunday算法 遵循匹配思路，失配时采取自己的优化策略，也尽可能的移动了最多的步数，达到提高效率的目的，且易理解。

后记

“字符串匹配算法”是“重学数据结构与算法”系列笔记：

• 字符串匹配算法(一)——BF算法
• 字符串匹配算法(二)——KMP算法
• 字符串匹配算法(三)——BM算法
• 字符串匹配算法(四)——Sunday算法