leetcode 周赛 184 - python 解答

5380.数组中的字符串匹配

暴力二重循环，因为 words 长度小于 100，肯定不会超时，但是注意每次找到了子串要 break，否则可能有重复。

class Solution:
    def stringMatching(self, words: List[str]) -> List[str]:
        ans = []
        for i in range(len(words)):
            for j in range(len(words)):
                if i == j: continue
                if words[i] in words[j]:
                    ans.append(words[i])
                    break
        return ans

5381.查询带键的排列

这题没有想到好的解法，直接写了最普通的模拟，本地试了下，还挺快的，应该会有更好的办法吧。

class Solution:
    def processQueries(self, queries: List[int], m: int) -> List[int]:
        m = min(m, max(queries))
        p = [i+1 for i in range(m)]
        ans = []
        for x in queries:
            i = p.index(x)
            ans.append(i)
            x = p.pop(i)
            p.insert(0, x)
        return ans

5382.HTML 实体解析器

这题对于 python 来说形同虚设。我直接用了替换函数，注意 python 的字符串是不可变类型，每次生成新对象。

class Solution:
    def entityParser(self, text: str) -> str:
        text = text.replace('"', '"')
        text = text.replace(''', '\'')
        text = text.replace('&', '&')
        text = text.replace('>', '>')
        text = text.replace('&lt;', '<')
        text = text.replace('&frasl;', '/')
        return text

感谢评论去两位同学指正，这个代码如果 遇到 > 输出的结果是 > ，但是这个实际上是把 & 转义出的 & 和 gt; 组合了，所以代码可以把 text = text.replace('&', '&') 放到最后一句以来避免，代码如下:

class Solution:
    def entityParser(self, text: str) -> str:
        text = text.replace('"', '"')
        text = text.replace(''', '\'')
        text = text.replace('&', '&')
        text = text.replace('>', '>')
        text = text.replace('&lt;', '<')
        text = text.replace('&frasl;', '/')
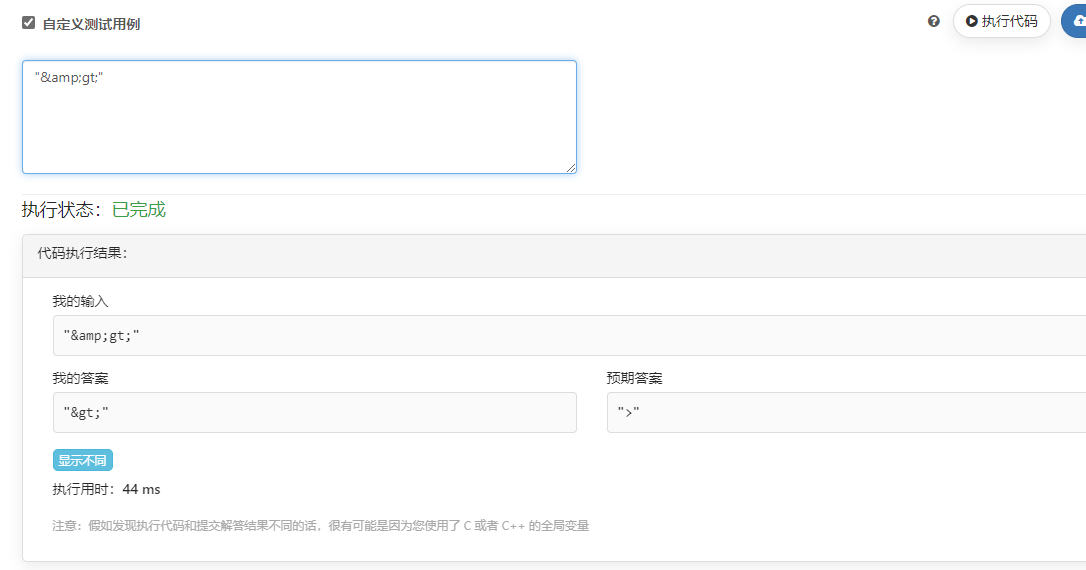
        return text

但是我又发现，判题系统目前对 > 的输出实际上是 >。
那么再试下 ">" 输出是 ">"，又没有递归处理，看了是判题机有问题。

5383.给 N x 3 网格图涂色的方案数

有一个很类似的题目，就是 一个 n 位的数组，每个位置可以填 0，1，2，但是相邻的不能重复，求一共有多少中填法。（好像还有点别的附加条件）

这道题目三种颜色没有任何区别，就用 ABC 来代表，n = 1 时
A 开头有：
ABA ABC ACA ACB
B 开头有：
BAB BAC BCA BCB
C 开头有：
CAB CAC CBA CBC

这里总结起来只有两种模式：ABA 即第一第三个一样 和 ABC 即三个都不同。

ABA 模式有 6 种：ABA ACA BAB BCB CAC CBC
ABC 模式有 6 种：ABC ACB BAC BCA CAB CBA

第二层需要再第一层的基础上安排，而且只和他的模式有关，而与具体颜色无关。

如果第一层是 ABA 模式（这个模式里的任意情况都会造成相同的结果）：

第一层   ABA   ABA   ABA   ABA   ABA
         |||   |||   |||   |||   |||
第二层   BAB   BAC   BCB   CAC   CAB

结果有 5 种，同样，我们只看模式，不看具体颜色，结果种有 ABA 模式 3 种，ABC 模式 2 种

如果第一层是 ABC 模式（这个模式里的任意情况都会造成相同的结果）：

第一层   ABC   ABC   ABC   ABC
         |||   |||   |||   |||
第二层   BAB   BCA   BCB   CAB

结果有 4 种，同样，我们只看模式，不看具体颜色，结果种有 ABA 模式 2 种，ABC 模式 2 种

我们代码里用 aba 表示当前层的 ABA 模式种数，abc 表示当前层 ABC 模式种数，而 aba2，abc2 表示下一层。这样就可以地推计算种类数量：

MOD = 1000000007
aba2 = (aba * 3 + abc * 2) % MOD
abc2 = (aba * 2 + abc * 2) % MOD

aba 和 abc 初始都为 6

class Solution:
    def numOfWays(self, n: int) -> int:
        aba = 6
        abc = 6
        MOD = 1000000007
        for _ in range(n-1):
            aba2 = (aba * 3 + abc * 2) % MOD
            abc2 = (aba * 2 + abc * 2) % MOD
            aba, abc = aba2, abc2
        return (aba + abc) % MOD

欢迎来我的博客： https://codeplot.top/
我的博客刷题分类：https://codeplot.top/categories/%E5%88%B7%E9%A2%98/