高中牛顿力学回顾
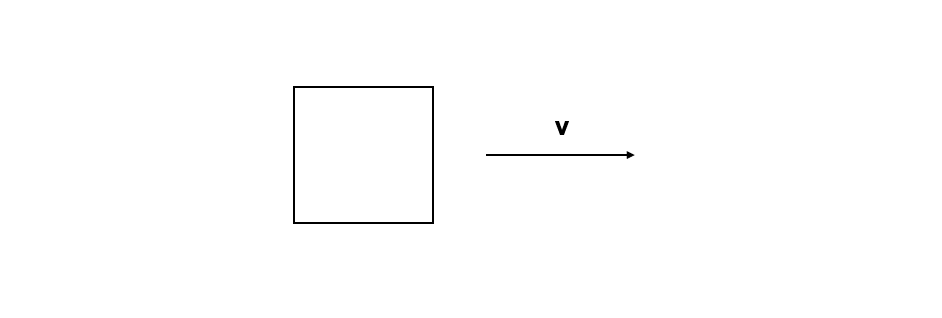
有一个具有一定速度在运动的物体:
当我们需要对其进行模拟时,自然会想起高中的 位移 = 速度 * 时间,即:
$$s = v * t$$
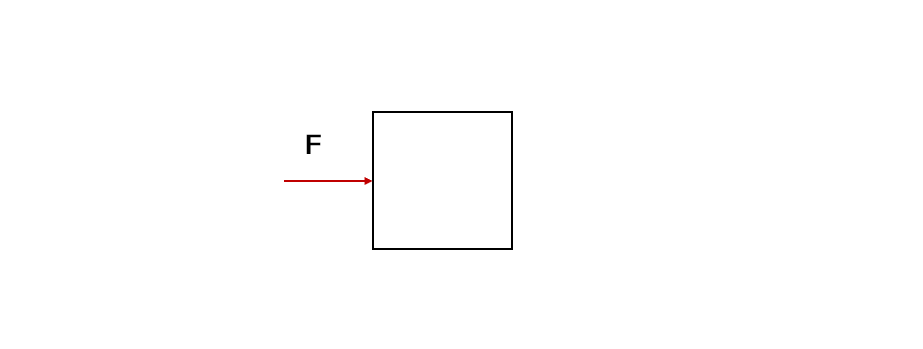
而当该物体具有恒定加速度(恒力)时:
我们可以应用牛顿第二定律,求出物体在 $t$ 时间的速度:
$$v_t = v_0 + \frac Fm * t$$
因此,我们想获得物体在 $t$ 时间的位置,就可以使用以下公式:
$$s = v_0 * t + \frac 12 * \frac Fm * t^2$$
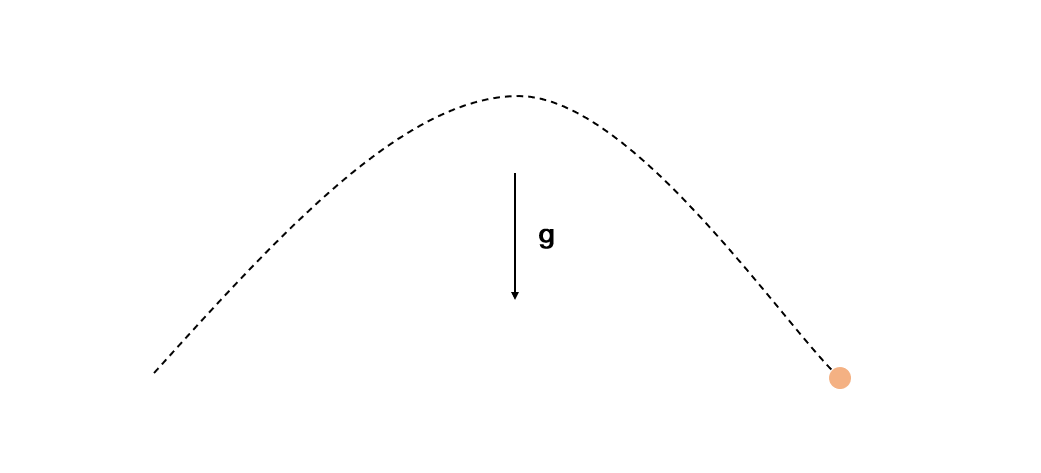
该公式在理想情况下,十分合理且正确,比如模拟一个斜方向向上抛出的小球,重力作用下(无空气摩擦),我们必定能得到一个对称的抛物线:
这都是高中物理课上我们学到的知识,对于简单的模拟已经够用了。
使用数值方法
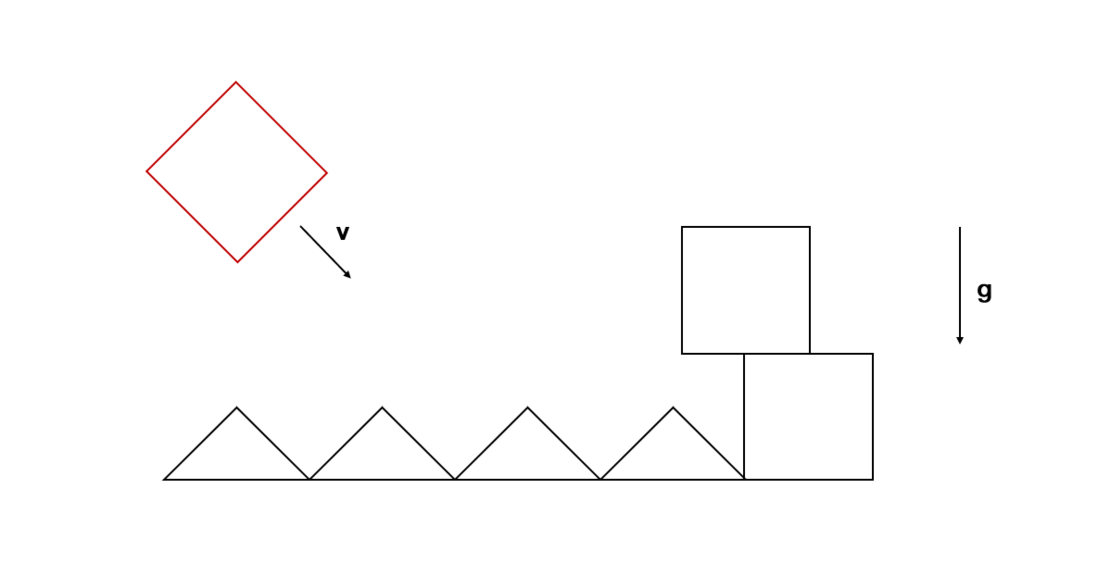
然而,我们要模拟的现实世界往往比较复杂,几乎不可能有受力恒定的情况出现,考虑以下情况:
你能写出红色盒子在之后的每一个时间 $t$ 的位置方程吗?显然这是无比困难的,因为该盒子受到的外力 $f$ 跟其位置 $p$ 有关,即 $f$ 与 $p$ 存在某种函数关系,因此,我们可以抽象出物体加速度 $a$ 与 $p$ 的关系:
$$a = \frac {f(t, p)} m$$
而又因 $a$ 为 速度 $v$ 的一阶阶导数,$v$ 为 $p$ 的一阶导数,因此我们最终得到:
$$\ddot p = \dot v = \frac {f(t, p)} m$$
这是一个标准的微分方程($p$ 上面有一点表示导数),我们从该方程中直接求出 $p$ 基本上是不可能的,因 $f$ 往往很复杂(包含了各种碰撞和约束) 。但是我们可以使用数值方法。数值方法的本质上是用某种方法来近似求出我们需要的解。使用数值方法我们得不到精确解,但是没所谓,在精度要求不是十分严格的模拟下一般都够用了。
而又物体的速度 $v$ 为 $p$ 的一阶导数,我们得到:
$$\dot p = v$$
我们可以将两条微分方程组合起来,使用矩阵表示:
$$\begin{bmatrix}\dot v \\ \dot p\\ \end{bmatrix} = \begin{bmatrix}\frac {f(t, p)} m \\ v\end{bmatrix}$$
用 $\dot X$ 表示左边的矩阵,$F(t, X)$ 表示右边的矩阵,有:
$$\dot X = F(t, X)$$
啰嗦了这么多,就是为了得到这个方程,我们的目标就是要使用数值方法求解出这个方程的 $X$。为什么要求 $X$?因为模拟的本质就是求某个物体在某一时候应该正确出现的位置(和旋转)。
求解微分方程的数值方法有许多,如 Runge Kutta,Mid-point,还有我之前介绍过的 Verlet,但我今天介绍最常用也是最基础的三种方法,分别为:
- 显式(向前)欧拉方法:Explicit Euler
- 隐式(向后)欧拉方法:Implicit Euler
- 半隐式欧拉方法:Semi-implicit Euler
显式(向前)欧拉方法
1. 介绍
观察我们的方程:
$$\dot X = F(t, X)$$
求解 $X$ 不容易,但是我们可以从 $\dot X$ 入手。
回忆高中数学,若有函数 $f(x)$,那么其导数的定义为:
$$\dot f(x) = \frac {df}{dx} = \lim_{h\to 0}\frac {f(x + h) - f(x)}{h}$$
但是计算机模拟是离散的,因此步长 $h$ 取不了无限小,只能是一个有一定大小的数,但是我们可以利用这种思想,对 $\dot f(x)$ 进行近似:
$$\dot f(x) \approx\ \frac {f(x + h) - f(x)}{h}$$
按照这种思路我们可以求出近似的 $\dot X$。
比如,我们要求 $t_1$ 时刻的 $\dot X$,我们可以:
$$\dot X_{1} = F(t_1, X_1) = \frac {X_2 - X_1}{t_2 - t_1}$$
其中 ${t_2 - t_1}$ 即模拟步长 $h$。那么现在我们可以求 $t_2$ 时刻的 $X$,即 $X_2$ 为:
$$X_2 = X_1 + h * F(t_1, X_1)$$
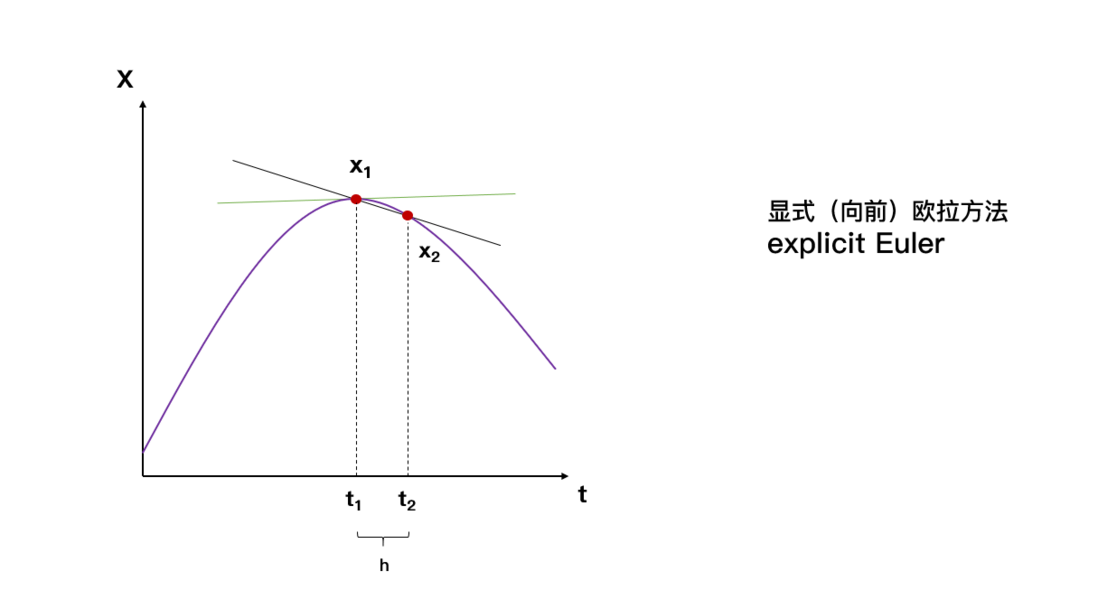
这种对于每一个时刻($t_2$),都使用上一时刻($t_1$)的解进行求解的方法即为显式欧拉方法,又叫向前欧拉方法。下图显示了显式欧拉方法的细节:
绿线为 $\dot X_{1}$ 的真实值,黑线为显式欧拉的得到的近似值,可以看到是有一定误差存在的,同时也能发现,缩短步长 $h$ 能提高精度。
显式欧拉简单高效且容易实现,但是缺点明显。
2. 稳定性分析
显式欧拉方法不是无条件稳定的方法。这句话我们要理解两个词,首先是稳定,第二是无条件。稳定指的是在长时间模拟下,得到的数值不会指数级爆炸;无条件指的是在任何微分方程下都能稳定。
因此显式欧拉方法在某些方程下能稳定,某些方程下不稳定。我们可以用以下方程来测试:
$$\dot y(t) = -\lambda y(t)$$ $$y(0) = \hat y$$
该线性微分方程称为测试方程,其中有初始值 $\hat y$,且 $\lambda > 0$。
该方程的解为 $y = \hat y e^{-\lambda t}$,显然在 $t \to +\infty$ 时,$y \to 0$。
我们将该测试方程代入到显式欧拉方法的公式里,有:
$$y_{t + 1} = y_t - h\lambda y_t = (1 - h\lambda)y_t $$
运用数学归纳法,我们可以得到 $y_t$ 与 $\hat y$ 的关系为:
$$y_t = {(1 - h\lambda)}^ty_t$$
显然,这是一个指数函数,因此想要在 $t \to +\infty$ 时不发生数值爆炸,我们只能限制:
$$\vert {1 - h\lambda} \vert < 1$$
也就是只有当 $h\lambda > 0$ 时或 $h\lambda < 2$ 时,不等式才能成立。
隐式(向后)欧拉方法
1. 介绍
显式欧拉方法的思路是使用上一时刻的导数($F(t - 1, X_{t - 1})$)去近似当前时刻的结果($X_{t}$)。而隐式欧拉对齐进行了改进:使用当前时刻的导数($F(t, X_{t})$)近似当前时刻的结果($X_t$)。这是隐式欧拉和显式欧拉的唯一区别。用公式表示就是:
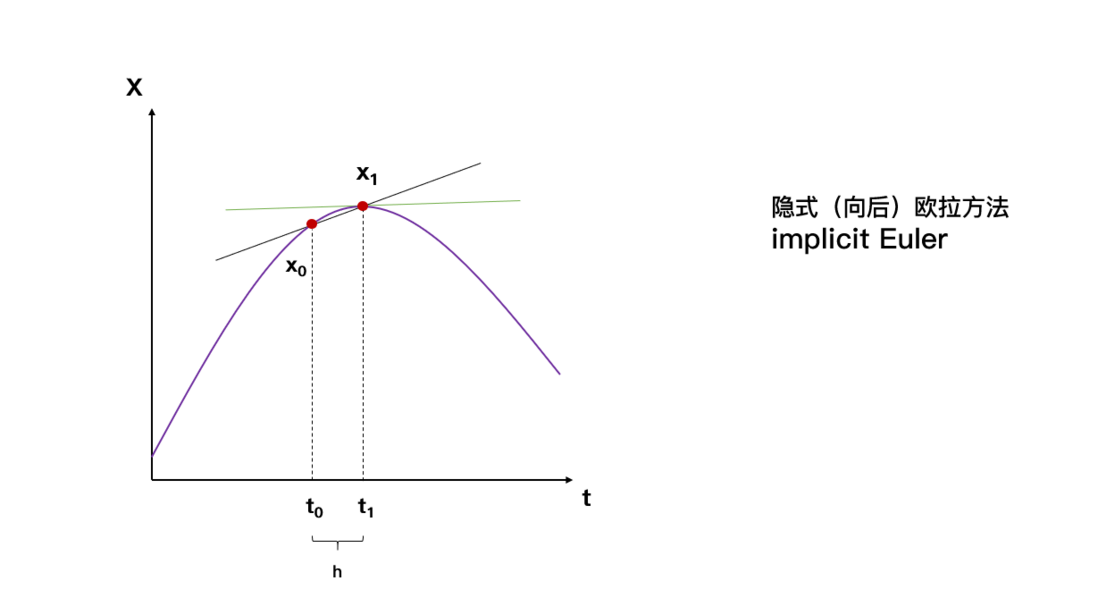
$$\dot X_{1} = F(t_1, X_1) = \frac {X_1 - X_0}{t_1 - t_0} $$ $$ \Rightarrow X_1 = X_0 + h * F(t_1, X_1)$$
绿线为 $\dot X_{1}$ 的真实值,黑线为隐式欧拉的得到的近似值,隐式欧拉同样也会产生误差。
也许你会发现一些问题:在 $X_1$ 未求出前,我们怎么能先计算 $F(t_1, X_1)$ 呢?没错这就是隐式欧拉方法最大的缺陷,它计算困难复杂,通常需要求解方程组,但是隐式欧拉最大的优点是数值稳定。
2. 稳定性分析
隐式欧拉方法是无条件稳定的方法。使用上面的测试方程,我们对隐式欧拉方法进行同样的操作:
$$y_{t + 1} = y_t - h\lambda y_{t + 1} $$
整理得:
$$y_{t + 1}(1 + h\lambda) = y\_t$$
对初始值 $\hat y$ 归纳得:
$$y_t = {(\frac {1}{1 + h\lambda})}^t \hat y$$
我们又得到了一个指数函数,同样想要不发生数值爆炸,只有:
$$\vert \frac {1}{1 + h\lambda} \vert < 1$$
也就是需要 $\vert 1 + h\lambda \vert > 1$。步长 $h$ 必定是一个正数,又有 $\lambda > 0$(上面有写),因此不等式恒成立。
半隐式欧拉方法
显式欧拉和隐式欧拉都有各种的缺点,因此后人想出了一种新方法,将两者结合了起来。
现在让我们忘记 $\dot X = F(t, X)$,回到:
$$\dot v = \frac {f(t, p)} m $$ $$ \dot p = v$$
对其使用显式欧拉积分,有:
$$v_{t + 1} = v_t + h * \frac {f(t, p_t)} m $$ $$ p_{t + 1} = p_t + h * v_t$$
既然对两条方程都使用隐式欧拉比较难求解,那么我们就仅对较简单的那条方程使用隐式欧拉:
红框显式了该方法与显式欧拉的唯一不同之处,我们使用显式欧拉求解速度,用隐式欧拉求解位置,这种混合的方法就叫半隐式欧拉方法。
半隐式欧拉方法相比于隐式欧拉方法更容易实现,速度更快,相比显式欧拉要更稳定些,但并不是无条件稳定。在大部分情况下半隐式欧拉方法都能稳定,除了某些极端条件(比如非常大的参数)。所以半隐式欧拉在刚体模拟下是最常用,也是首推的。
总结
- 显式欧拉:简单,快,不稳定
- 隐式欧拉:复杂,慢,稳定
- 半隐式欧拉:简单,快,大部分情况稳定(刚体模拟首推)
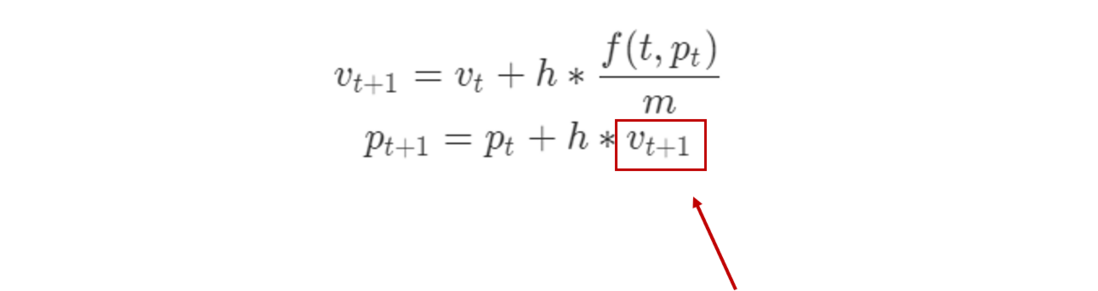
**粗体** _斜体_ [链接](http://example.com) `代码` - 列表 > 引用。你还可以使用@来通知其他用户。