利用包围盒的交集筛选分离轴

咸鱼了好多天，快开学了，还是要输出点东西的。

回顾

在19年7月的时候，我曾经写过一篇有关分离轴筛选的文章，其基本思想是利用 多边形的分解算法，将多边形分解为三角形，将多边形的边相交问题收敛为粒度更小的三角形相交问题，从而得到更精确的潜在分离轴。
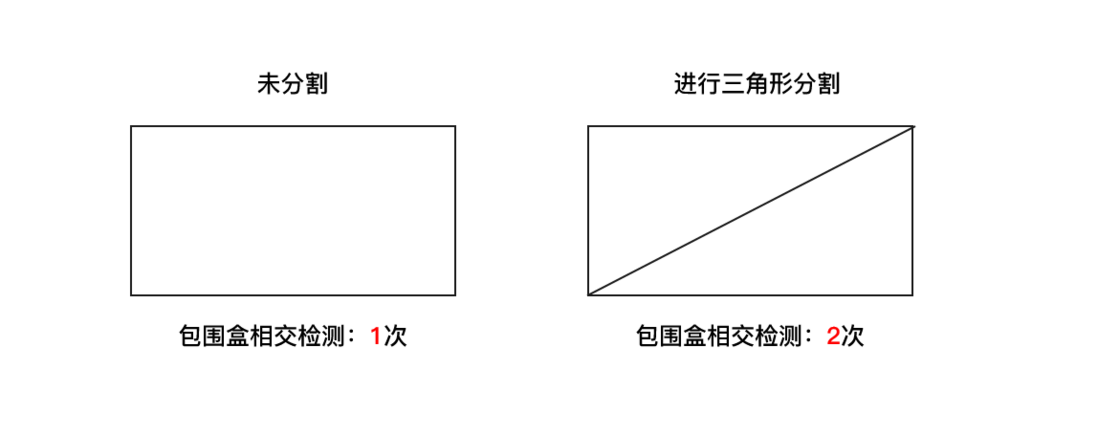
当然这种方法在理论上是可行的，但是在简单多边形（如矩形）的判定下，可能效果会适得其反。如下图，在未进行分解前，对一个矩形进行包围盒检测只需要一次，但在分解后，由于矩形分解为三角形只能沿着对角线切割，所以分解出的两三角形的包围盒和矩形的包围盒是完全一样的，因此也就是多做了一次多余的包围盒检测。

当然这个问题有解决的办法吗，当然有，我只要限制5条边以下的多边形不做分解不就可以了吗。

但是我仍觉得这种方法没有深入到问题的本质上，我要的目标是什么，是要在进行分离轴检测前，把那些“不可能”的分离轴都预先剔除掉，因此进行多边形分解，只是手段而不是目的。我可能过于关注如何更好地分解多边形，从而掉进了一个思维陷阱。

多边形分解固然可行，但是较为复杂，不仅要对每一个多边形先执行一次分解算法，还要为每一个三角形单独维护一个包围盒。其实我更应该思考的是如何更优地寻找“边”（边和轴是一一对应的关系），如果有一种方法可以更快速地筛选出最可能的边，那么我根本就不需要分解多边形。

包围盒的交集

其实在那篇文章就不难看出，两凸多边形相交时，分离轴往往隐藏在两凸多边形中相交的那些子三角形中，这个结论很重要，由此我们可以由此进一步推断，分离轴就是两凸多边形相交的那些边的法向量的其中一条。

基于此结论，我们现在大可以抛掉那些多边形分解的东西了，而将关注点转移到寻找相交的边上。线段相交的判定算法有很多，然而，我们不需要真的对两多边形的每一条边都进行相交检测，因为这是一种非常暴力的解法，通常复杂度为O(n^2)，我们最终还是要回归到分离轴算法，但我们可以大概知道哪些边可能会发生相交。

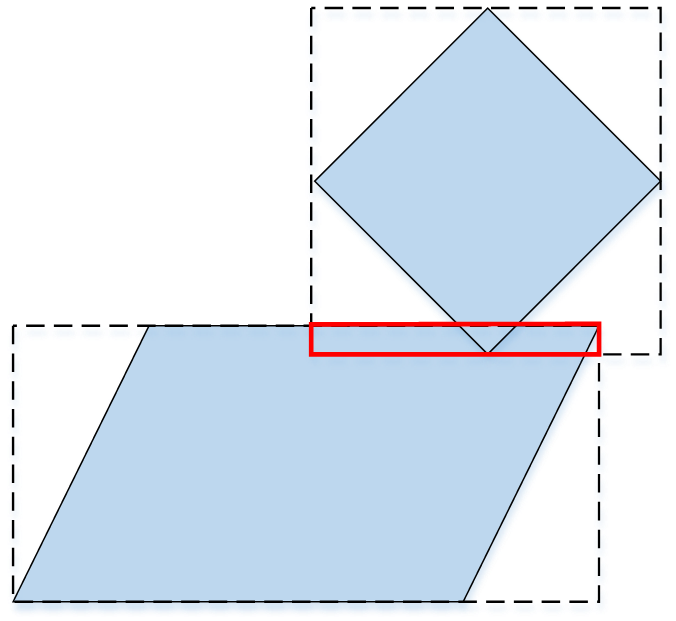
通常情况下，我们使用包围盒进行粗检测的时候，仅仅只是是判断两包围盒是否发生了相交（true/false），而很少去关注两个包围盒相交的交集部分（intersection）。如下图：

图中红色矩形表示两包围盒的交集矩形。观察图中，我们不难发现：

交集中恰好就隐含了两多边形发生相交的边

这是一个十分有用的性质，这意味着我们只要找到包围盒的交集，就能找到可能发现相交的边，也就能迅速筛选出最可能成为分离轴的那些轴。

该思路与多边形分解相比，具有明显的优势。首先，求解包围盒的交集的算法（O(1)）比起多边形分解算法(O(n))要简单很多。其次，我们不需要刻意地预先计算包围盒的交集，只需要在粗检测阶段将返回的布尔值改为包围盒交集（intersection/null）即可。

具体步骤

在基于两多边形的包围盒已经发生相交的情况下，首先判断包围盒交集矩形的水平和垂直深度，然后利用交集矩形深度最小的边，分别向两边作延长线。最后，计算两延长线与多边形相交的边，这些边的法线便是最有可能的轴，称为最优潜在轴，其余边的法线都是可以剔除的无效轴。

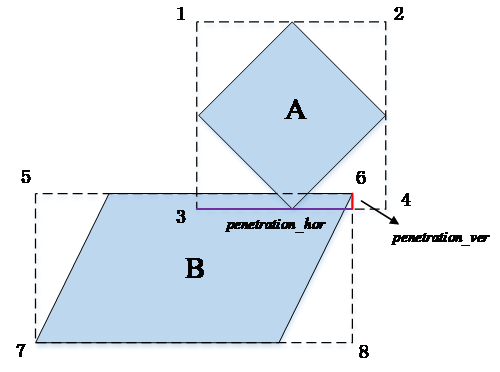
如下图所示，有两凸多边形A，B，且A，B在碰撞检测粗检测阶段下已确定其包围盒相交，A的包围盒的四个角分别为1，2，3，4，B包围盒四角为5，6，7，8。

该算法的具体步骤如下：

Step1. 因A，B包围盒相交产生的交集矩形的会有水平相交深度penetration_hor和垂直相交深度penetration_ver。如下图所示的情况，penetration_hor为图中紫色的线，penetration_ver为图中红色的线。明显，penetration_ver < penetration_hor。

Step2. 因penetration_ver < penetration_hor，所以选取产生penetration_ver的两天包围盒边作为切割线。对于A的包围盒，是边3-4，对于B的包围盒，是边5-6。如下图，将边3-4和边5-6分别向两端延长，分别得到切割线cl_A和cl_B。

Step3. 计算潜在边。计算B中与cl_A相交或以cl_A为分界线靠近A的边，计算A中与cl_B相交或以cl_B为分界线靠近B的边。如下图所示，A中红色两边与cl_B相交，因此该两边成为潜在边；B中左右两红色斜边与cl_A相交，成为潜在边。同时，以cl_A为一条分界线，将B分为两部分，显然B顶部的边是靠近A的，因此顶部的边也成为潜在边。

Step4. 计算最优潜在轴。对Step2得到的所以潜在边求对应的法向量，这些法向量就是全部的最优潜在轴。如下图所示。

最后在分离轴算法中使用计算出的最优潜在轴进行检测即可。

分析

我们可以发现该算法剔除轴的核心在于两条切割线的与多边形边的位置关系。因此，不难判断，当多边形越复杂（边数越多时，该算法的剔除效果越好），因为边数越多，边就越短，受切割线影响的边就越少。

上一节的例子中，两多边形共有8条边，最终得到的最优潜在分离轴有5条，剔除了3条，剔除率为37.5%，看起来效果差强人意。

然而当两多边形边数足够多时，算法的优化效率就会提高。如下图所示，A为有10条边的多边形，B为有9条边的多边形，共有19条边。使用本文提出的算法后，共得到5条潜在边，剔除14条边，剔除率为73%。剔除率相比上一节的例子大大提升。

相关文献

我在网上找了一下，发现国内外对这方面的探索和研究并不多，只找到一篇与本人研究相关的文章：

Cheng Liang等提出了一种基于多边形最近点的分离轴算法优化方案，将潜在的最近点投影在两多边形重心的连线上，然后根据投影是否发生重叠来判断是否发生了碰撞，且能剔除部分不可能的轴。

然而，该方案虽比直接AABB相交检测要更加精确，但却需预先计算重心和遍历所有顶点确定最近点，存在比较繁琐且昂贵的预计算。