前言
我们首次接触广度优先搜索和深度优先搜索时,应该是在数据结构课上讲的 “图的遍历”。还有就是刷题的时候,遍历二叉树/拓扑排序我们会经常用到这两种遍历方法。
广度优先搜索算法(Breadth-First-Search,缩写为 BFS),是一种利用队列实现的搜索算法。简单来说,其搜索过程和 “湖面丢进一块石头激起层层涟漪” 类似。
深度优先搜索算法(Depth-First-Search,缩写为 DFS),是一种利用递归实现的搜索算法。简单来说,其搜索过程和 “不撞南墙不回头” 类似。
BFS 的重点在于队列,而 DFS 的重点在于递归。这是它们的本质区别。
1. 广度优先搜索法
广度优先搜索,也叫做广度优先遍历,其主要思想类似于树的层序遍历。
- 从任意一个节点A开始,遍历它的全部的邻接点B,C
- 然后再以它其中一个邻接点B为起点,遍历B的所有的邻接点D,F。
- 然后再以它另外一个邻接点C为起点,遍历C的所有的邻接点G,H。
- 然后再以它其中一个邻接点D为起点,遍历D的所有的邻接点...。
- 以此类推....
伪代码如下:
public void bfsSearch(){
//定义一个结果集,queue队列
List<Node> queue = new LinkedList<Node>();
//先选择一个出发点,加入队列。
queue.add(nodeA);
int size = queue.getSize();
for(int index=0;index<size;index++){
//BFS的重点在于队列,它的思路就是沿着queue的添加顺序,依次遍历他们的邻接点。
for(Node node : queue.get(index).getNeighbor()){
//没被搜索过,那么加入结果集
if(!queue.contain(node)){
queue.add(node);
size = queue.getSize();
}
}
}
}
BFS比较适合判断二分图,以及用于实现寻找最小生成树(MST),如在BFS基础上的Kruskal算法。还有寻找最短路径问题(如Dijkstra算法)。
1.1 无向图的广度优先遍历
我们先给出一个图:
- 先找到A,这是第一层。
- 再找到A的邻接点,遍历到B,C,D,F。
- 再找到B,C,D,F的邻接点,遍历到G,E,H
1.2 有向图的广度优先遍历
思路和与无向图类似,只不过需要考虑边的走向问题。
- 先找到A,这是第一层。
- 再找到A的邻接点,遍历到B,C,F。
- 再找到B,C,F的邻接点,遍历到D,H
- 再找到D,H的邻接点,遍历到E,G
2. 深度优先搜索法
深度优先搜索,也叫做深度优先遍历,其主要思想是回溯法,它的核心是使用递归。
例如这张图,从1开始到2,之后到5,5不能再走了,退回2,到6,退回2退回1,到3,以此类推;
伪代码如下:
//stack:定义的结果集stack栈
//currentNode:本次递归搜索的当前node
public void dfsSearch(Stack<Node> stack,Node currentNode){
if(currentNode没有邻接点 && !stack.contain(currentNode)){
//压入结果栈
stack.push(currentNode);
return;
}
//node有邻接点,那么遍历邻接点,依次深搜
for(Node node : currentNode.getNeighbor()){
if(node.isVisited() || stack.contain(currentNode)){
continue;
}
node.setVisited(true);
dfsSearch(stack,node);
node.setVisited(false);
}
//currentNode的邻接点都已经遍历过了,现在逻辑回溯回currentNode
//那么需要将currentNode压入结果栈
stack.push(currentNode);
}
2.1 无向图的深度优先遍历
我们先给出一个图:
对上无向图进行深度优先遍历,从A开始:
第1步:访问A。
第2步:访问B(A的邻接点)。 在第1步访问A之后,接下来应该访问的是A的邻接点,即"B,D,F"中的一个。但在本文的实现中,顶点ABCDEFGH是按照顺序存储,B在"D和F"的前面,因此,先访问B。
第3步:访问G(B的邻接点)。 和B相连只有"G"(A已经访问过了)
第4步:访问E(G的邻接点)。 在第3步访问了B的邻接点G之后,接下来应该访问G的邻接点,即"E和H"中一个(B已经被访问过,就不算在内)。而由于E在H之前,先访问E。
第5步:访问C(E的邻接点)。 和E相连只有"C"(G已经访问过了)。
第6步:访问D(C的邻接点)。
第7步:访问H。因为D没有未被访问的邻接点;因此,一直回溯到访问G的另一个邻接点H。
第8步:访问(H的邻接点)F。
因此访问顺序是:A -> B -> G -> E -> C -> D -> H -> F
2.2 有向图的深度优先遍历
对上有向图进行深度优先遍历,从A开始:
第1步:访问A。
第2步:访问(A的出度对应的字母)B。 在第1步访问A之后,接下来应该访问的是A的出度对应字母,即"B,C,F"中的一个。但在本文的实现中,顶点ABCDEFGH是按照顺序存储,B在"C和F"的前面,因此,先访问B。
第3步:访问(B的出度对应的字母)F。 B的出度对应字母只有F。
第4步:访问H(F的出度对应的字母)。 F的出度对应字母只有H。
第5步:访问(H的出度对应的字母)G。
第6步:访问(G的出度对应字母)E。 在第5步访问G之后,接下来应该访问的是G的出度对应字母,即"B,C,E"中的一个。但在本文的实现中,顶点B已经访问了,由于C在E前面,所以先访问C。
第7步:访问(C的出度对应的字母)D。
第8步:访问(C的出度对应字母)D。 在第7步访问C之后,接下来应该访问的是C的出度对应字母,即"B,D"中的一个。但在本文的实现中,顶点B已经访问了,所以访问D。
第9步:访问E。D无出度,所以一直回溯到G对应的另一个出度E。
因此访问顺序是:A -> B -> F -> H -> G -> C -> D -> E

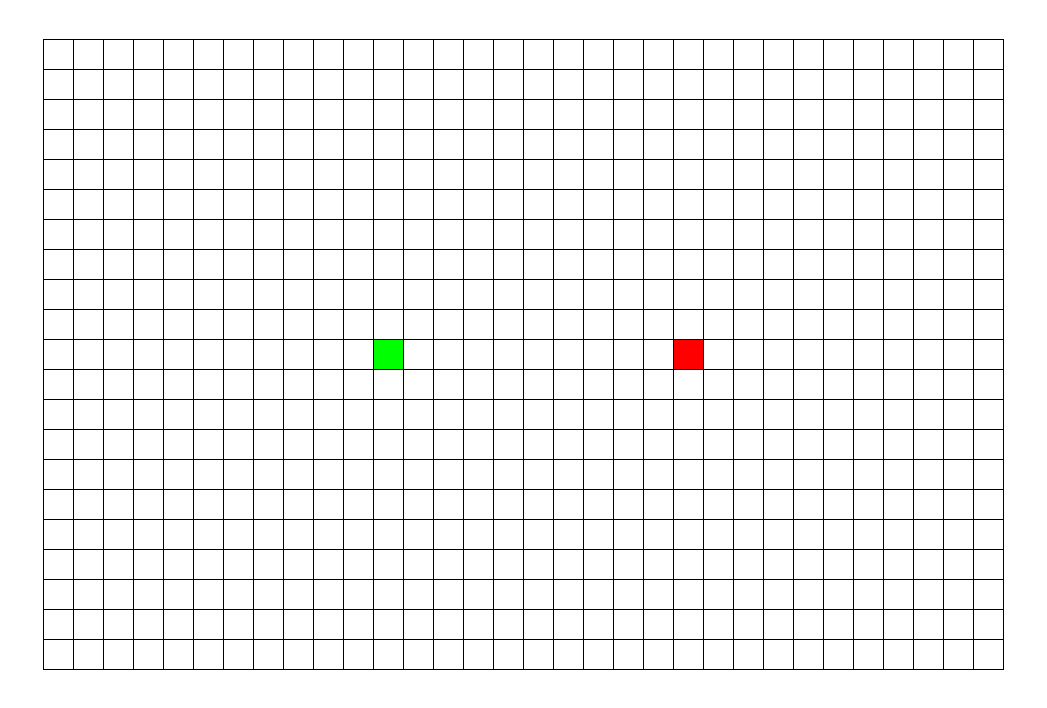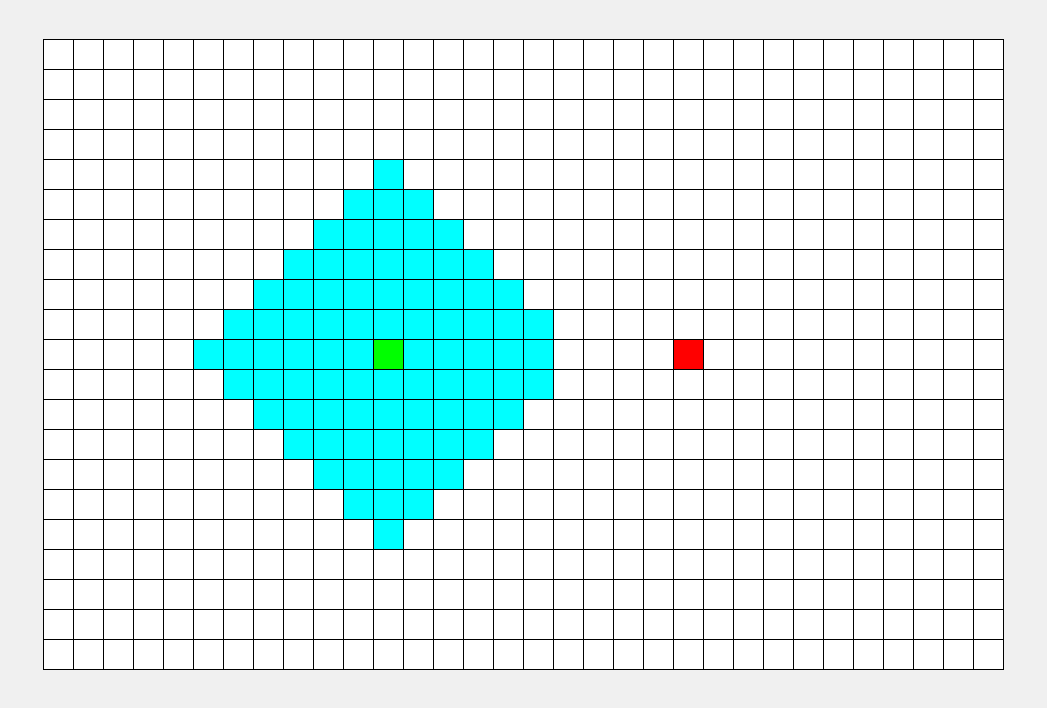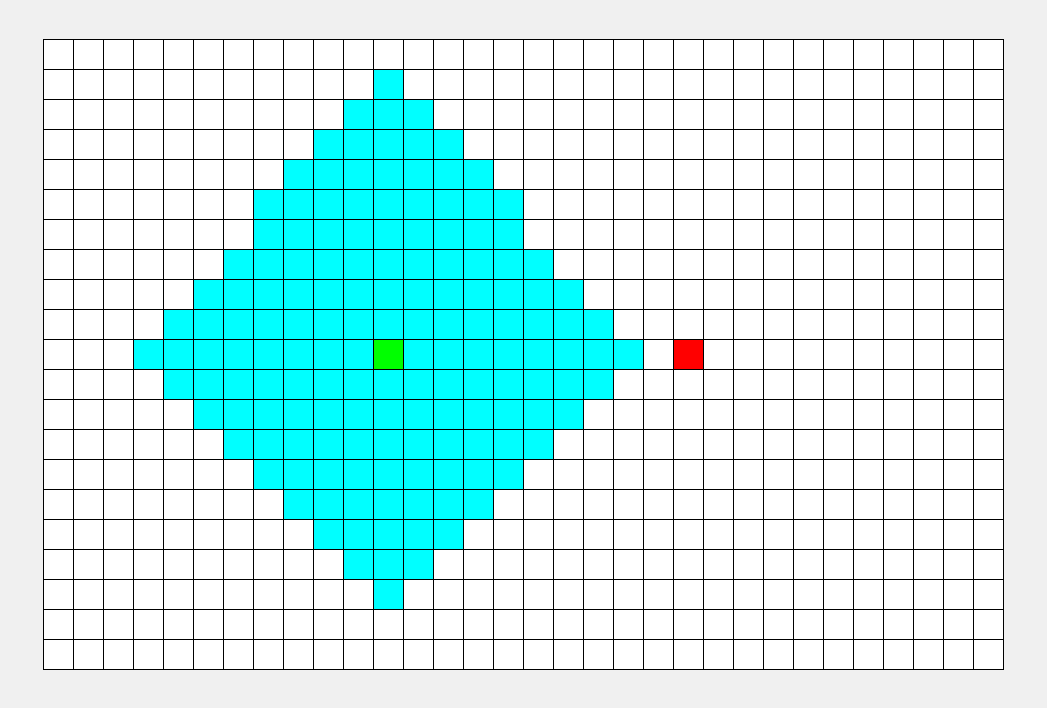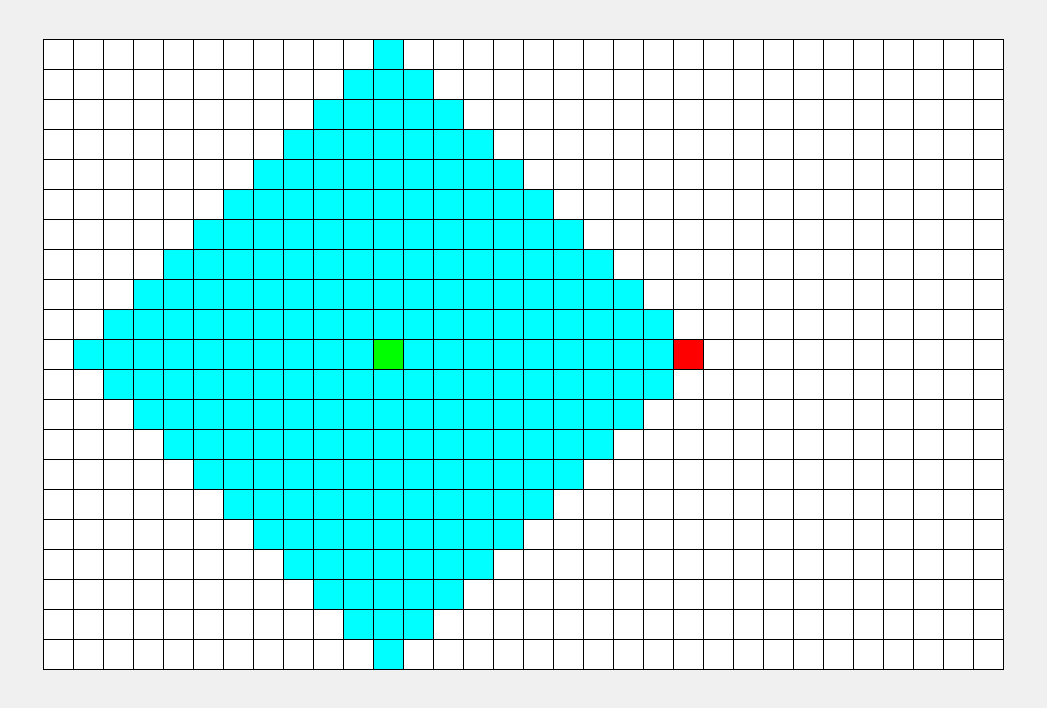







**粗体** _斜体_ [链接](http://example.com) `代码` - 列表 > 引用。你还可以使用@来通知其他用户。