关于从入门three.js到做出3d地球这件事(第五篇: 以点成面矢量地球)有图解

关于从入门three.js到做出3d地球这件事(第五篇: 以点成面矢量地球)

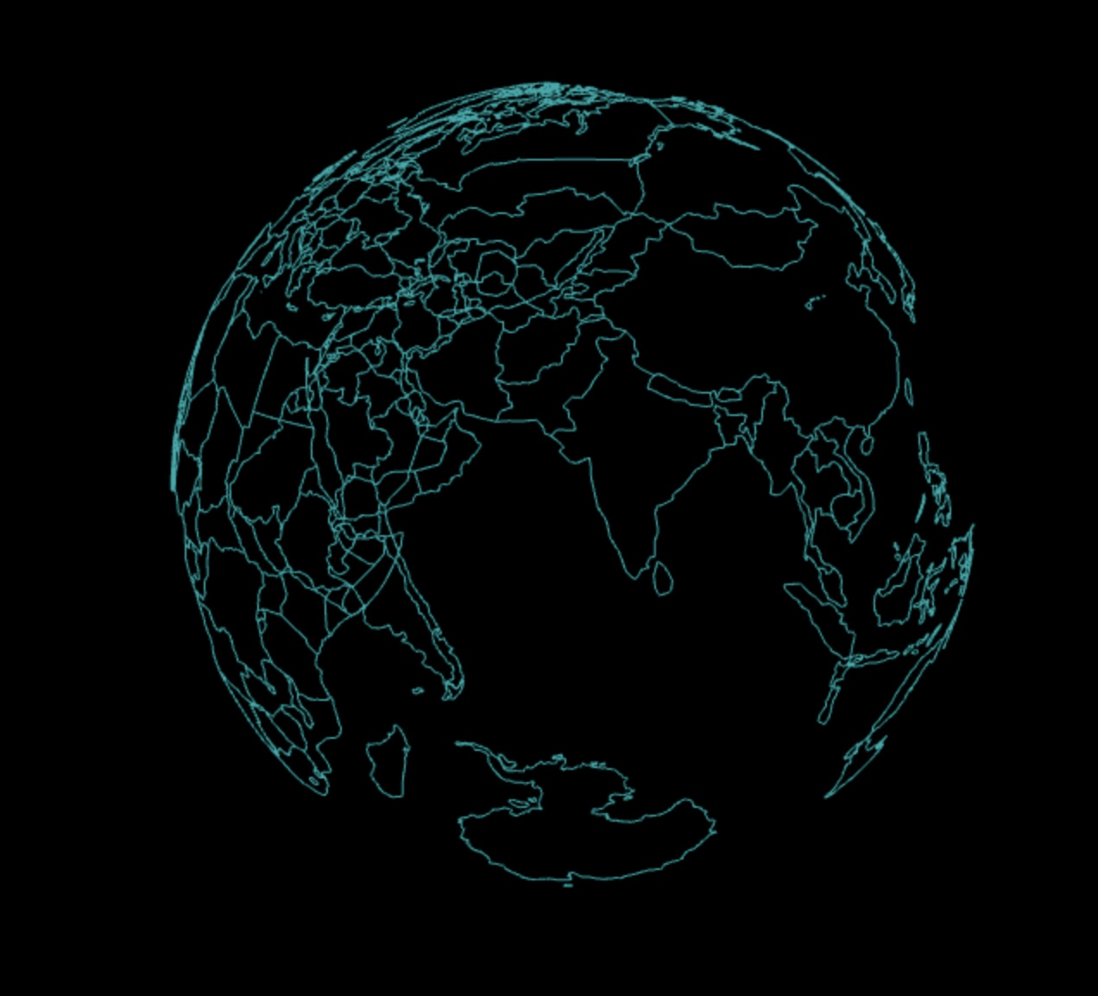
本篇效果图:

注: 本人画工较差哈哈哈哈哈哈...

一. `geojson`基本概念

本篇我们要绘制一个矢量地球, 那我们先要知道矢量地球是由什么组成的, 比如说要绘制'中国', 那么我们只要知道中国边界上所有的点的坐标, 再逐一把这些点链接起来就是一个中国的轮廓了, 由于每个点相距很近所以虽然我们是用直线链接但依然可以形成圆滑的球面效果, 简单理解geojson就是这样一组数据, 它里面有绘制各个国家轮廓所需的所有的点的信息, 深入理解你会发现geojson里面还有各种分组信息, 但我们本篇主要讲绘制最基本的国家轮廓就不展开讨论了, 让我们先绘制一款平面地图。
这是我之前写过的一篇详细介绍geojson的文章,有兴趣的同学可以去了解下, 会有助于你更好的理解地图: 记一次前端"揭开绘制地图的神秘面纱"分享会。
本章设计的数学知识都是初级的, 再往后会涉及到矩阵之类的知识, 到时候我也会用最通俗的方式解释给你听, 绝不止于概念而是最通俗的方式方便你理解, 本篇后面会有详细的经纬度转xyz的讲解与图解。

二. 经纬度

这里的概念很基础也很重要, 如果不熟悉的话要仔细看哦。

经度

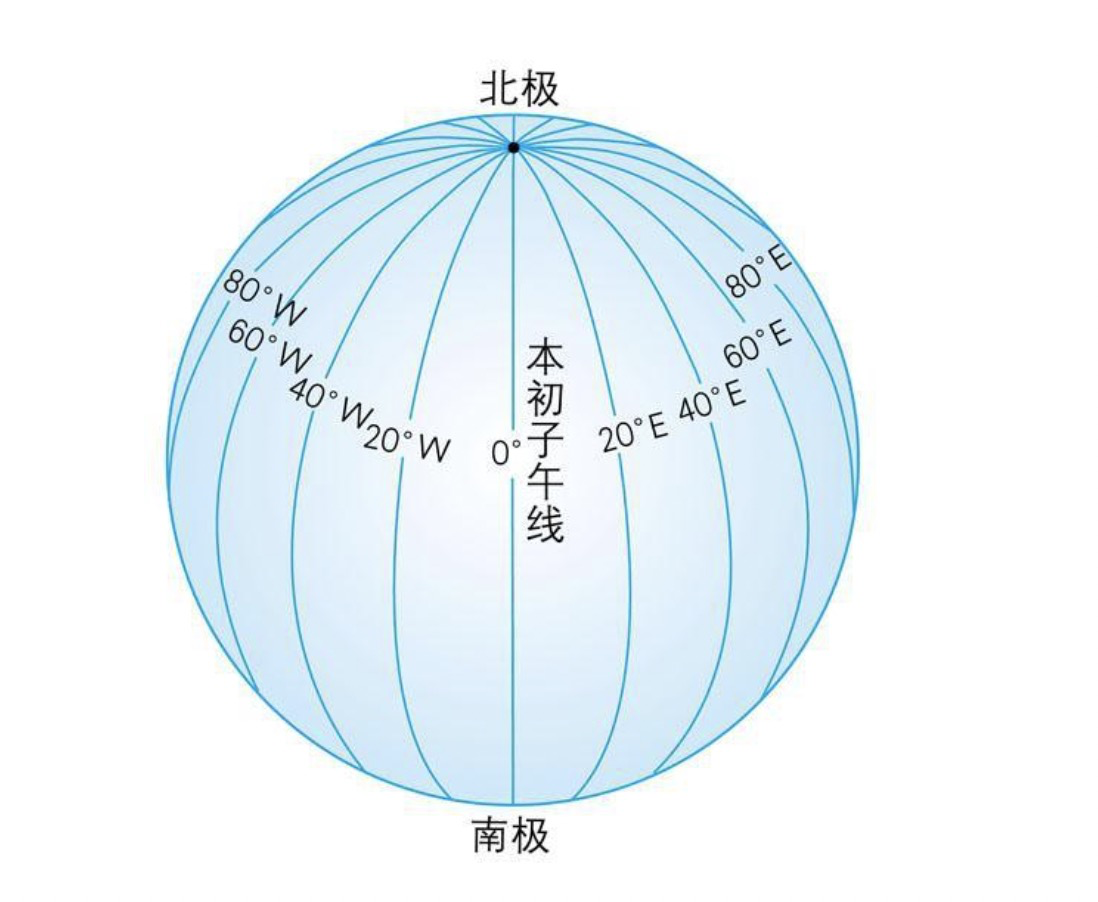
经度是地球上一个地点离一根被称为本初子午线的南北方向走线以东或以西的度数。本初子午线的经度是0°，地球上其它地点的经度是向东到180°或向西到180°, 做为本初子午线的那条线是人选出来的, 每15°一个时区(时区引起的bug我在之前分享过: 时区相关bug)。
如图所示, 在计算机里面是用正负数来区东经与西经, 东经为正数西经为负数, 度数范围是[-180, 180]。

纬度

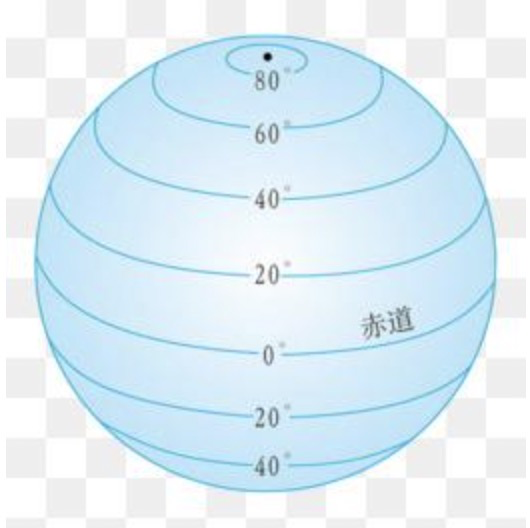
过椭球面上某点作法线，该点法线与赤道平面的线面角，其数值在0至90度之间。位于赤道以北的点的纬度叫北纬，记为N；位于赤道以南的点的纬度称南纬，记为S。
如图所示, 在计算机里面是用正负数来区北纬与南纬, 北纬为正数南纬为负数, 度数范围是[-90, 90]。

扩展知识: 测量经纬度

在地球上任何地点，只要有只表，有根竹竿，一根卷尺，就可知道当地经纬度。但表必须与该国标准时校对, 具体方法在百度百科有兴趣的可以做下实验。

三. 还记得三角函数么

大郎不要怕我们毕业这么久也不用背诵了, 只要知道怎么用就行, 我们一起来复习一下:

名称	公式
sin(∠A)	a/c
cos(∠A)	b/c
tan(∠A)	a/b

因为geojson里面存储的数据是经纬度, 所以等下我们要用他把经纬度转换成坐标, 当然geojson也可以直接储存坐标。

四. 弧度

即两条射线从圆心向圆周射出，形成一个夹角和夹角正对的一段弧。当这段弧长正好等于圆的半径时，两条射线的夹角的弧度为1。

五. 前端代码里的实现

如果你想当然认为直接在前端代码里写入Math.sin(30)就会输出0.5那你就错了。

因为在我们的Math运算里面, 需要输入的是弧度, 这就是为啥我上面要复述弧度的概念, 所以想求sin(30)我们要这样写Math.sin(30 * Math.PI / 180)。

为了方便大家都能理解我还是简单写下推导过程

1弧度是对应弧长为半径的角度, 已知一个圆的周长是 2πr。
可以得出结论, 一个圆总共有 2πr ÷ r 个弧度, 也就是2π弧度为一个圆。
一个圆有360°角, 1°的角度对应的弧度就是 2π÷360, 也就是 π/180。
所以上面所说的sin(30°)就是Math.sin(30 * Math.PI / 180)

六. 绘制一个平面世界

学到这里我默认你已经了解了geojson的相关概念, 里面一个国家可能有多个轮廓并且互相不接壤, 我们要把它们处理成数组, 也就是这句country.geometry.type === "Polygon"。
/cc_map_3d_pro/src/components/cc_map.vue

import worldGeo from "../assets/geojson/world.geo";
.../
    initEarth() {
      const R = envConifg.r;
      worldGeo.features.forEach((country) => {
        if (country.geometry.type === "Polygon") {
          country.geometry.coordinates = [country.geometry.coordinates];
        }
        var line = countryLine(R, country.geometry.coordinates);
        this.scene.add(line);
      });
    },

世界的geojson可以在我的项目里找到github查看。

上面我们把半径, 点位传给了countryLine方法来处理, 并且把他们都加入到了环境里面, 后面会讲把图形对象都分别放入不同的组里面, 这里先这样不扩散知识点。

七. 用`点`绘`线`

/cc_map_3d_pro/src/utils/countryLine.js这个方法里我们专门绘制国家的轮廓。

import * as THREE from 'three';

function countryLine(R, polygonArr) {
  let group = new THREE.Group();
  polygonArr.forEach(polygon => {
    let pointArr = [];
    polygon[0].forEach(elem => {
      pointArr.push(elem[0], elem[1], 0)
    });
    group.add(line(pointArr));
  });
  return group;
}

`new THREE.Group()`

在three.js中文网接摘下来的原话, 它几乎和Object3D是相同的，其目的是使得组中对象在语法上的结构更加清晰。

假设我现在生成两个正方体geometry, 分别命名为a 与 b, 那么我不用下面的写法

this.scene.add(a);
this.scene.add(b);

而是可以创建一个组:

const group = new THREE.Group();
group.add(a)
group.add(b)
this.scene.add(group);

再详细的我们后续章节会详细聊。

上面我们依赖了一个名为line的方法, 这个方法是这次的一个重要的知识点。

八 . 绘制线段不简单(`line`方法)

function line(pointArr) {
  let geometry = new THREE.BufferGeometry();
  let vertices = new Float32Array(pointArr);
  let attribue = new THREE.BufferAttribute(vertices, 3);
  geometry.attributes.position = attribue;
  let material = new THREE.LineBasicMaterial({
    color: 0x00aaaa //线条颜色
  });
  let line = new THREE.LineLoop(geometry, material);
  return line;
}

1. 传入的参数`pointArr`;

由countryLine方法可知, 这里是[x1, y1, z1, x2, y2, z2, x3, y3, z3]这样的一系列坐标, 你可能感觉这种形式不太符合js的思想, 但是它符合webgl或是svg的思想, 关于webgl的知识后续会在讲解着色器的时候会让你明白的, 现在不用太深研究因为这里学问很深。

2. `new THREE.BufferGeometry()`;

使用BufferGeometry可以有效减少向GPU传输上述数据所需的开销, 一个国家平均有几百组点, 所以再用普通的Geometry会变的很卡, 大家放心后续在 优化 相关的篇幅里面我会统一讲一遍, 这里你可以暂时理解为一种three.js转换的数据流。

3. `new Float32Array()`;

js原生知识: Float32Array类型数组代表的是平台字节顺序为32位的浮点数型数组(对应于 C 浮点数据类型), Float32Array在数据量较大时性更更好一些, 并且更符合webgl的参数标准, 关于这类TypedArray是个大课题, 详细的我会在着色器章节好好聊聊。

4. `new THREE.BufferAttribute()`;

这个类用于存储与BufferGeometry相关联的 attribute（例如顶点位置向量，面片索引，法向量，颜色值，UV坐标以及任何自定义 attribute), 利用 BufferAttribute可以更高效的向GPU传递数据。

第一个参数: 是数据源, 也就是上面处理好的坐标数组。
第二个参数: 数据被存储为任意长度的矢量, 这里传的是3, 可以理解为每三个数据为一组, 也就是x1, y1, z1一组, x2, y2, z2一组, 以此类推。

5. `new THREE.LineBasicMaterial()`;

基础线条材质, 也就是专业绘制线条的, 可以调节颜色与粗细, 以及线头的样子。

6. `geometry.attributes.position = attribue`

这个写法看起来很粗鲁, 它的意思就是把图形的位置信息, 替换成我们处理好的数组, 也就是为图形设置每个点的位置。

7. `new THREE.LineLoop()`;

环线也就是首尾相连的线, 就向我们每次创建一个矩形一样, 这个方法创建了一条环线。

由于我们把z轴的数值都传的0, 所以才会出现下图这种平面地图

九. 经纬度转换到笛卡尔坐标系(理论)

也有不少库是直接做这种平面地球的, 但我们的系列文章是要学习圆形地球的, 所以我们要把经纬度坐标转换成球面坐标。
我们就从x y z逐一开始研究。

最简单的`y轴`

y轴其实只与纬度有关, 最简单就可以求出来如下图所示:

球体上的一个点, 这个点距离圆心的距离是圆的半径r, 现在我们要求这个点距离zy平面的距离。

这个点的x与z不一定为0, 所以作垂线不一定落在x轴上, 但是不管如何作垂线这条线段与xz平面的夹角是不会变的, 而这个夹角就是纬度, 所以由此可知我们已知斜边的长度为r, 三角函数sin(纬度) = 对边 / 斜边, 对边就是y轴的数值, 我们把使用左右都乘以r, 最终得出:
```
sin(纬度) 乘 r = y
```

需要计算的`x轴`

x轴需要点计算我们一步一步来, 每步都有图解:

上面演示的是, 我们可以把这个点看成是一个立方体, 一个已知对角线长度为r的立方体, 接下来我们就可以把这个立方体单独拿出来研究, 可以脱离这个坐标系了。

现已知立方体对角线长度为r, 高为y轴坐标, 接下来使用纬度求出底面对角线。

我们采用与求y轴差不多的方式求出x1的长度:

cos(纬度) 乘 r = x1

由图可知经度是下方沿yz平面展开的对角线的角度, 我们可以用sin的对边比斜边求出长度。

sin(经度) * x1 = x

把x1的公式带入进来:

x = sin(经度) 乘 cos(纬度)

与x对应的`z轴`

与x相同的原理,只是这里我们用cos的临边比斜边。

z = cos(经度) 乘 cos(纬度)

十. 经纬度转换到笛卡尔坐标系(代码)

实战的时候别忘了, 先把经纬度转成弧度。

// 经纬度转坐标
function lon2xyz(R, longitude, latitude) {
    const lon = longitude * Math.PI / 180;
    const lat = latitude * Math.PI / 180;
    const x = R * Math.cos(lat) * Math.sin(lon);
    const y = R * Math.sin(lat);
    const z = R * Math.cos(lon) * Math.cos(lat);
    return { x, y, z };
}
export default lon2xyz;

一些其他教程

一些其他教程会要求 经度取反, 同时把x与z进行颠倒,不推荐那种写法, 我们就按正常的思路来即可。

十一. 圆圆的地球

经过不懈的努力我们终于拯救了圆球, 让我们看看他还缺什么吧:

从上图我们可以看出, 其实问题还是挺多的, 比如线条之间互相遮盖, 我们应该让这个地球不可透视, 以及暂时这个地球不可点击, 并且真实度上做的不够, 真是技术路漫漫那。

end

下一篇就要讲解如何在地图上打点以及为地球添加光晕等等效果, 到此时这个系列文章还不到一半哦, 射线拾取国家以及三角抛分方面的知识也会陆续付出水面, 精彩有趣的知识还在后面, 希望与你一起进步。

关于从入门three.js到做出3d地球这件事(第五篇: 以点成面矢量地球)有图解