2D Matrix: What kind of monsters are these all!

The head "bald" comes from " the book of shader "

My article today may be a bit abstract. I try my best to "have pictures and the truth" so as not to let everyone's brain memory leak!

This article will talk about:

• The mathematics behind transform 2D transform
• How to understand a matrix intuitively
• What is homogeneous transformation?
• Some may be involved: inverse matrix ( ), orthogonal ( ), vector knowledge, just pretend you know it when you use it!
• But basically it will not involve 3D, quaternion, MVP matrix transformation in various engines. Don't say much, let's start

I want all scale+skew+rotate

As a traditional front-end, a senior csser must know that in the transform attribute, it is possible to configure rotate for rotation, scale for zooming, and skew for beveling.

Furthermore, transform also provides operations such as matrix and matrix3d so that we can transform graphics more freely:

So we can probably think of 2D rotate, scale, and skew, which are actually some kind of special matrices.

So the next step is how to write these three operations in matrix form.

However, before we think about it, what is the basic unit of matrix operation?

Is "dot"

Points make up lines, and lines make up faces!

If you have written a shader, you will know that gl also manipulates a bunch of points to generate a screen.

So "the goddess zoomed in are all mosaics

Of course! There may be mosaics without magnification (error)

Now that the unit of matrix operation is a "point", what is the result of any point p(x,y) after a matrix change?
2D:

3D:

The formula in the figure above represents matrix multiplication:

Matrix*matrix, the right matrix can be regarded as a splicing of two points/vectors. Multiplication rules remain unchanged
Now let's take a look at the matrix corresponding to scale/skew/rotate:

For the simplest scale matrix, (x, y) is transformed by the scaling matrix and we expect it to become (scaleX x, scaleY y), which is verified by formula 1 above:

For the rotation matrix, this represents the angle between the vector after counterclockwise rotation and the original vector.

Let us verify, suppose that for p0(1,1) then it will become p1(0,√2) after being rotated =45 degrees:

The oblique matrix is also a similar routine, the angle is changed from one to two. We will mention this later. Readers can also verify by themselves.

At present, although we have written the three transformations of scale, skew, and rotate as matrices, they are still independent. Human beings are always greedy, can they only use one way to understand them? In other words, we want to know what the corresponding matrix is for any transformation (arbitrary here is actually not very rigorous, we will talk about this later)?

It is necessary to introduce a new concept:

"base" vector (must use a purple)

We know that the matrix is actually changing the "point", how do we represent a point in space?

In the 2D Cartesian coordinate system, two mutually perpendicular directions constitute the x-axis and the y-axis. Any point P is represented by a logarithm (a, b). For example, (2,3) means a certain point in 2D space. What is the meaning of 2,3 here?

Here 2 means that p occupies 2 units of length in the x direction, and 3 means that occupies 3 units of length in the y direction. These two unit lengths are represented by vectors as [1,0]^T and [0,1]^T.

In this view, the point can be written as: 2 [1,0]^T + 3 [0,1]^T:

T is transpose. It can be understood that the row vector originally written horizontally is written vertically as a column vector. Look! It's like the picture below.

Generalize to arbitrary coordinates (a, b):

｜1 0｜｜a｜    
｜0 1｜｜b｜ 

Among them, [1,0]^T and [0,1]^T are called a set of basis vectors. The matrix they formed actually has a name called the identity matrix.

The identity matrix actually has many important properties in more complex interactions, but it has nothing to do with today's topic. Just listen to it!

Understand matrices high-level

We now bring the "base vector" and the points represented by the "base vector" into the linear transformation, and see how the base vector changes after one transformation?

Here we found an interesting phenomenon:

The original basis vectors x0, y0 are transformed into 1, 1 (the red part in the figure above). The original point P0 becomes P1 after transformation. At this time, the point p1 can be described by 1, 1. The coefficients before 1, 1 are still the coefficients of the original p0(a,b). (Although the shape has changed, the ratio of the red dotted grid to the basis vector in the figure remains unchanged)

Organized into mathematical language is:

Give a "chestnut":

For a zoom operation, the x-axis is magnified by 1.5 times and the y-axis is magnified by 2 times.

[x] = [1.5,0]^T

[y] = [0,2]^T

Then the matrix corresponding to the transformation is:

｜x y｜ = ｜1.5  0 ｜   =  ｜scaleX   0    ｜
         ｜ 0    2 ｜     ｜   0   scaleY ｜

In the same way, rotation and slanting transformation can also use the idea of base vector, and it is easy to get the corresponding matrix:

This includes but is not limited to the matrix transformation of rotate/scale/skew, we can all understand from the perspective of the basis vector.

Speaking of which, the knowledge points about 2D matrices are roughly over! ?

Is there something weird?

I can't move!

Correct! We did not explain translate at all. The 2*2 matrix we have so far can only perform the following operations

The point [x,y] can only be transformed into the form of [a x+c y,b x+d y]^T.
This kind of transformation is called linear transformation. Linear transformation has two obvious characteristics:

• Linearity: For the matrix transformation to observe any point in the space, they will be affected in the same way. Or to put it loosely, the grid will not become a curve after transformation (as shown in the figure below), nor will it be uneven: part of it is enlarged, and the other part is reduced.

• Symmetry about the origin:

No matter how the basis vector changes in the figure, the origin does not change.

This property is actually well understood, the point [0,0] is [0,0] no matter what matrix is used for processing, which means that the matrix transformation is actually not capable of translation operations.

Because the algebraic nature of linear transformation is:

Ran goose! The algebraic nature of the translation operation is:

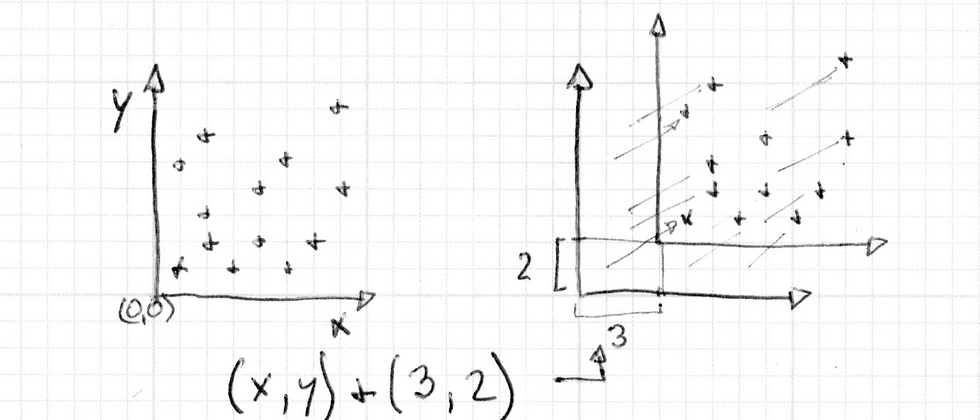
At this time, only a 2D matrix is used and I want to translate. It's really "the concubine can't do it", so at this time we introduce a new transformation "homogeneous transformation"!

Homogeneous transformation

Why did you say that it was 2D and turned it into 3D for me? Although we extend the original 2-dimensional point [x,y] to a three-dimensional point [x,y,1].

But we don't have to worry about the third row, we can only look at the first two rows of the matrix:

In fact, it is the matrix (a, b, c, d, tx, tx) in css. And the result of this matrix transformation really realizes 2D linear transformation and translation:

At this point, the principle part of the transformation of the 2D matrix is basically finished. Below we combine the source code of PIXI.js for some simple source code analysis:

Bald link

PIXI.js uses the combination of transform+matrix to implement graphics operations.
Let's take a look at Matrix.ts. .

export class Matrix
{
// ......
  constructor(a = 1, b = 0, c = 0, d = 1, tx = 0, ty = 0)
    {
        /**
         * @member {number}
         * @default 1
         */
        this.a = a;

        /**
         * @member {number}
         * @default 0
         */
        this.b = b;

        /**
         * @member {number}
         * @default 0
         */
        this.c = c;

        /**
         * @member {number}
         * @default 1
         */
        this.d = d;

        /**
         * @member {number}
         * @default 0
         */
        this.tx = tx;

        /**
         * @member {number}
         * @default 0
         */
        this.ty = ty;
    }
// .....
}

You can see that the parameters of this constructor are the same as the first two rows of the homogeneous transformation matrix we mentioned above, and they are also consistent with the matrix parameters in css.

But its comments are still easy to cause some misunderstandings:

/**
     * @param {number} [a=1] - x scale
     * @param {number} [b=0] - y skew
     * @param {number} [c=0] - x skew
     * @param {number} [d=1] - y scale
     * @param {number} [tx=0] - x translation
     * @param {number} [ty=0] - y translation
*/

There is no need to stick to the specific purpose of each parameter, we can now accurately understand it from the perspective of the basis vector.

Most of the methods of matrix are relatively easy to understand, let's pick a few and talk about it!

rotate(angle: number): this
    {
        const cos = Math.cos(angle);
        const sin = Math.sin(angle);

        const a1 = this.a;
        const c1 = this.c;
        const tx1 = this.tx;

        this.a = (a1 * cos) - (this.b * sin);
        this.b = (a1 * sin) + (this.b * cos);
        this.c = (c1 * cos) - (this.d * sin);
        this.d = (c1 * sin) + (this.d * cos);
        this.tx = (tx1 * cos) - (this.ty * sin);
        this.ty = (tx1 * sin) + (this.ty * cos);

        return this;
    }

The function of rotate is to rotate, and the matrix itself also records a set of transformations. Then on this basis, the operation needs to use matrix multiplication. The multiplication of matrices is sequential. For example, if we need to perform translation, zoom, and translation operations on the points as shown in the figure, we must multiply the matrices in sequence:

The rotate operation is performed after the original matrix, so the new matrix is [Result] = Rotate:

Is it suddenly clear?

Yes it is! Except for some special operations, most normal humans are not willing to face matrix calculations, so PIXI provides another class of Transform. The matrix transformation is replaced by some easy-to-understand attributes (position, scale, rotate...) (CSS heavy transform also has similar effects), the Transform code is also more business, the data on it is ObservablePoint, and it also implements the parent and child Level relationship. In actual operation, Transform realizes the conversion between its own data and Matrix data through the decompose method.

decompose(transform: Transform): Transform
    {
        // sort out rotation / skew..
        const a = this.a;
        const b = this.b;
        const c = this.c;
        const d = this.d;
        const pivot = transform.pivot;

        const skewX = -Math.atan2(-c, d);
        const skewY = Math.atan2(b, a);

        const delta = Math.abs(skewX + skewY);

        if (delta < 0.00001 || Math.abs(PI_2 - delta) < 0.00001)
        {
            transform.rotation = skewY;
            transform.skew.x = transform.skew.y = 0;
        }
        else
        {
            transform.rotation = 0;
            transform.skew.x = skewX;
            transform.skew.y = skewY;
        }

        // next set scale
        transform.scale.x = Math.sqrt((a * a) + (b * b));
        transform.scale.y = Math.sqrt((c * c) + (d * d));

        // next set position
        transform.position.x = this.tx + ((pivot.x * a) + (pivot.y * c));
        transform.position.y = this.ty + ((pivot.x * b) + (pivot.y * d));

        return transform;
    }

Among them Math.atan2(-c, d) and Math.atan2(b, a). In fact, the angle before and after the transformation of the two basis vectors is calculated:

When ø is equal to, we consider this to be a rotation operation. However, due to the problem of numerical precision, it is difficult for floating-point numbers to be equal, so PIXI uses the difference method to judge, that is

var delta = Math.abs(ø -  )；
if(delta < Number.EPSILON){
   ...
}else{
   ....
}

It should be noted here that the x basis vector determines the slanting value in the Y direction, while the y basis vector determines the slanting value in the X direction:

I think this is the most amazing thing in this code.

Because the skewX we calculated is actually in the negative direction. And delta = Math.abs(ø-) needs to take the difference between the two values. PIXI directly adds symbols to Math.atan2(-c, d). The subsequent judgment directly uses delta = Math.abs(skewX + skewY); and the skewX direction is also corrected. This kind of code integration and ingenuity is in fact all over PIXI.js, and I really admire the author's logical ability.

Finally, talk about scale and position

The position is the normal homogeneous transformation.

For scale, the criterion for judging whether there is scaling is whether the basis vector is scaled, so scale.x is the modulus length of the x basis vector after rotation (a a+b b) ^0.5

The same is true for scale.y.

The above are some of the knowledge points about the 2D matrix that I have summarized. I hope you will give me your advice.

Suddenly I found that we haven't talked about the shader for a long time. In the next issue, let's talk about how to realize the water mist and frosted glass shader.

Reference materials:

Fundamentals of Computer Graphics, Fourth Edition
​
"The Essence of 3blue1Brown Linear Algebra"

thebookofshaders