【有点简单】不靠矩阵也能旋转和平移？

2D矩阵对旋转的局限性在之前的文章中我们讨论过旋转这件事，也说过用2阶矩阵描述的旋转：
教练我想学矩阵
很多成熟的框架/库也是基于矩阵这套逻辑来写的，比如说我膜拜的pixi.js

{
            // get the matrix values of the displayobject based on its transform properties..
            lt.a = this._cx * this.scale.x;
            lt.b = this._sx * this.scale.x;
            lt.c = this._cy * this.scale.y;
            lt.d = this._sy * this.scale.y;

            lt.tx = this.position.x - ((this.pivot.x * lt.a) + (this.pivot.y * lt.c));
            lt.ty = this.position.y - ((this.pivot.x * lt.b) + (this.pivot.y * lt.d));
            this._currentLocalID = this._localID;

            // force an update..
            this._parentID = -1;
}

但是很明显使用二阶矩阵有两个问题，第一旋转操作只能应用于原点，我们无法使用二阶矩阵完成绕任意点转动的计算，第二遇到平移操作时我们需要拓展成齐次矩阵（这部分可以回看之前的文章）第一个问题其实在引入奇次矩阵后就可以解决，只要先把旋转点A平移到0，绕原点旋转𝛉，再把0平移回旋转点A。

这套逻辑虽然也够用，但更多情况下我们只需要处理绕某个原点外的点旋转的逻辑即可。
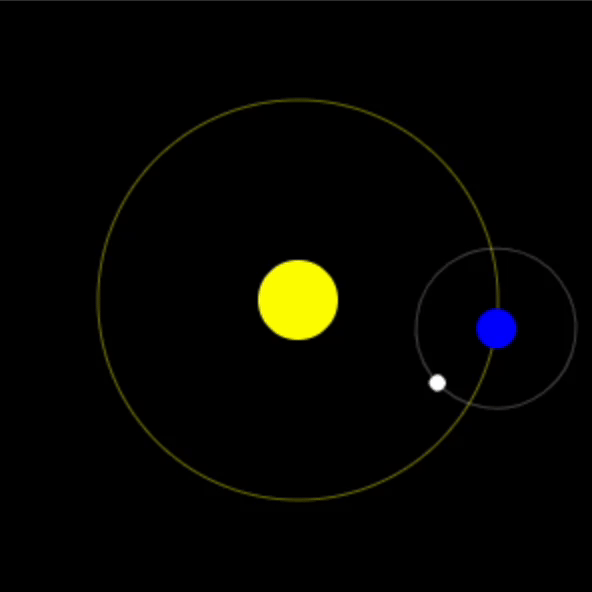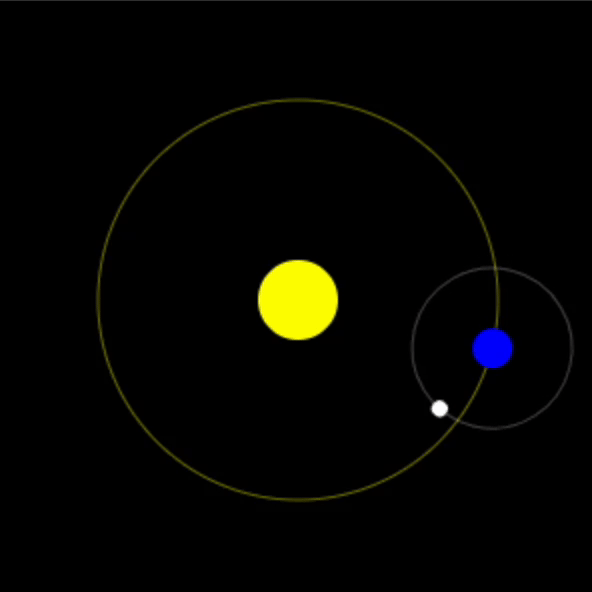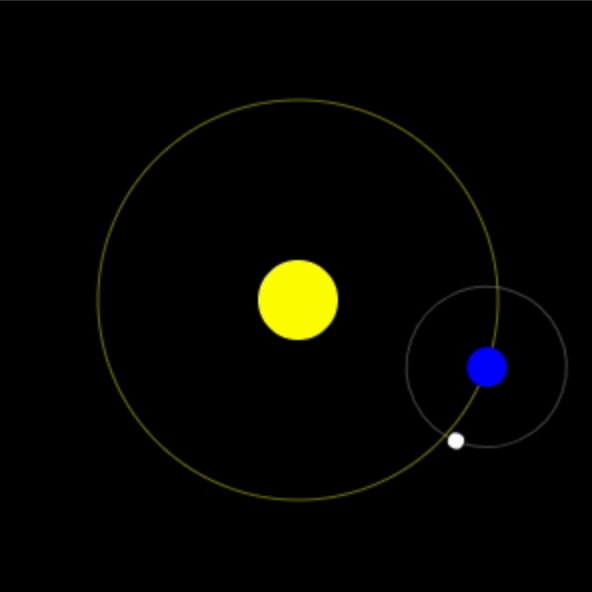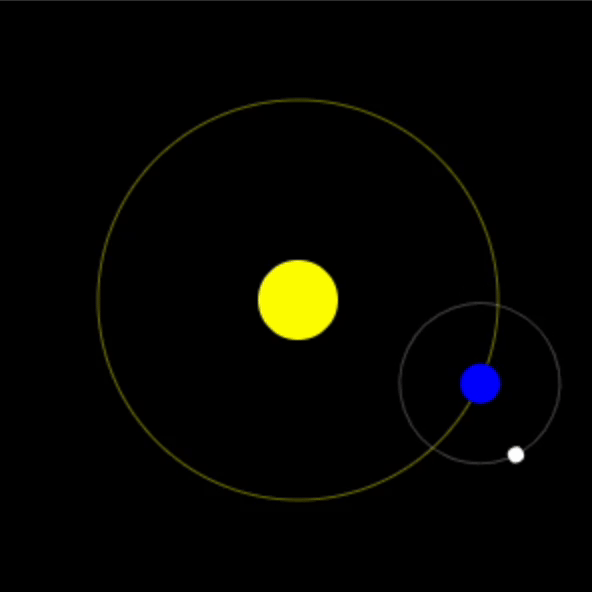
比如下图模拟一个地月日系统时处理月球绕地球的旋转。

有没有更优雅的形式呢？还真有那用复数。复数与复平面复数是什么？

复数与复平面

复数就是一个定义在复平面上的数，复平面类似我们的直角坐标系，只不过x轴上是实数单位，y轴上是虚数单位（就是高中数学里面那个√-1）

这个复平面上的一个点表示方法又很多比如可以用x轴y轴对应的长度表示成数系：(a,b)
可以分解成xy轴(类似物理力的分解\( )：a cos\theta + b\bar{i}sin\theta \)
注意这里的加号并不表示两者能相加只是个记号
还可以表示成类似极坐标的形式：\( re^{i\theta} \)
同时由于复数是一个数，它还可以进行四则运算。
加法：
\( z_{A}+z_{B} = (x_{A},y_{A})+(x_{B},y_{B}) = (x_{A}+x_{B},y_{A}+y_{B}) \)

这不就是平移操作？就是A点向x方向平移了\( x_{B} \)向y方向平移了\( y_{B} \)
乘法：
\( z_{A}z_{B}=(Ae^{i\alpha})(Be^{i\beta}) = ABe^{i(\alpha+\beta)} \)
他的几何意义：

A绕原点逆时针旋转了\(\beta\)而长度增加了B倍。看到这里是不是DNA动了？

复数体系内缩放/旋转/平移是闭合的。不过我们今天不聊缩放只着墨于旋转+平移。

复数描述平移与旋转

平移操作

我们使用记号\( T_{v}(z) \)表示将平面上的一个复数z移动v，即：\( T_{v}(z) = z + v \)。\( T_{v} \)的逆向操作就是\( T_{v}^{-1} \)。
由于\( T_{v}(z)T_{v}^{-1} (z)= T_{v}^{-1}(z)T_{v}(z)=z \)所以\( T_{v}^{-1}= T_{-v} \)
而复合的平移可以写成：
\( T_{v}\circ T_{w}(z) = T_{v}(z+w)=z+(w+v) \)

旋转操作

对于旋转操作我们可以定义绕a旋转𝛉为\( R_{a}^{\theta} \)而显然\( R_{a}^{\theta}R_{a}^{\vartheta}=R_{a}^{\theta+\vartheta} \)，\( (R_{a}^{\theta})^{-1} = R_{a}^{-\theta} \)。而绕原点的旋转则可以写成
\( R_{0}^{\theta}(z)=e^{i\theta}z \)
那么怎么求出这个\( R_{a}^{\theta} \)，我们可以套用矩阵时的思路，把先把a平移到0, 绕原点旋转𝛉, 再把0平移回a:
\( R_{a}^{\theta}(z)=T_{a}\circ R_{a}^{\theta}\circ T_{a}^{-1}(z)=e^{i\theta}(z-a)+a=e^{i\theta}z+k \)
其中\( k=a(1-e^{i\theta}) \)
这就意味着，绕任何点的旋转都可以写成绕原点的旋转再加上一个平移量。然后这个操作还是封闭的。

那么连续绕两个不同的点旋转？
\( (R_{a}^{\alpha}\circ R_{b}^{\beta}) (z)= e^{i(\alpha+\beta)}z+v 其中 v=be^{i\alpha}(1-e^{i\beta})+a(1-e^{\alpha}) \)
\( 当(\alpha+\beta) \ne 2k\pi 时：\)
\( (R_{a}^{\alpha}\circ R_{b}^{\beta}) (z)=R_{c}^{\alpha+\beta} 其中 c= \frac{v}{1-e^{i(\alpha+\beta)}}=\frac{be^{i\alpha}(1-e^{i\beta})+a(1-e^{\alpha})}{1-e^{i(\alpha+\beta)}} \)
\( 当(\alpha+\beta) = 2k\pi 时 e^{i(\alpha+\beta)}=1\)
\( (R_{a}^{\alpha}\circ R_{b}^{\beta}) =T_{c} 其中 c=(1-e^{i\alpha})(b-a) \)

几何解释

最后我们再从几何直观上理解下这两个过程，绕点a旋转后再绕点b旋转，在数学上可以证明总能找到另外一点c使得绕c点旋转\( (\alpha+\beta) \)与绕点a旋转后再绕点b旋转等价：

而 时，就是按连接第一个旋转中心到第二个旋转中心的复数的2倍作平移：

代码层面

代码层面反而是最简单的，乞丐版只需要实现一个类complexNumber即可，在内部有一个方法add和multi，对外只需要暴露一个rotate方法即可：

class complexNumber {
  _real: number;
  _imaginary: number;
  constructor(real: number, imaginary: number) {
    this._real = real;
    this._imaginary = imaginary;
  }
  private _add(a:complexNumber,b:complexNumber):complexNumber{
    return new complexNumber(a._real+b._real,a._imaginary+b._imaginary);
  }
  private _mul(a:complexNumber,b:complexNumber):complexNumber{
    const real = a._real*b._real-a._imaginary*b._imaginary;
    const imaginary = a._real*b._imaginary+a._imaginary*b._real;
    return new complexNumber(real,imaginary);
  }
  private sub(a:complexNumber,b:complexNumber):complexNumber{
    return new complexNumber(a._real-b._real,a._imaginary-b._imaginary);
  }
  public rotate(angle:number,z:complexNumber):[number,number]{
    const p = new complexNumber(Math.cos(angle),Math.sin(angle));
    const v:complexNumber = this._mul(z,this.sub(new complexNumber(1,0),p));
    const result:complexNumber = this._add(this._mul(p,this),v);
    return [result._real,result._imaginary]
  }
}