算法（leetode，附思维导图 + 全部解法）300题之（5）最长回文子串

零 标题：算法（leetode，附思维导图 + 全部解法）300题之（5）最长回文子串

一 题目描述

二 解法总览（思维导图）

三 全部解法

1 方案1

1)代码：

// 方案1 滑动窗口法（“时间复杂度高，一般通过不了”）
var longestPalindrome = function(s) {
    // 是否为 回文串。（subStr = '' 稍微体现下编程的严谨性）
    const isValid = (subStr = '') => {
        const l = subStr.length;
        let resFlag = true;

        // 边界：i < l/2
        for(let i = 0; i < l/2; i++) {
            // “对称位置”上的字符不相等，那么肯定就不是 回文串 了
            if (subStr[i] !== subStr[(l - 1) - i]) {
                resFlag = false;
                break;
            }
        }

        return resFlag;
    }

    const l = s.length;
    // curMaxLength 当前回文子串的最大长度，范围：[l, 1]
    for (let curMaxLength = l; curMaxLength > 0; curMaxLength--) {
        // 在 curMaxLength 下，curStartIndex的有效范围为 [0, ((l + 1) - curMaxLength) )
        for (let curStartIndex = 0; curStartIndex < ((l + 1) - curMaxLength); curStartIndex++) {
            const subStr = s.substr(curStartIndex, curMaxLength);
            // 一旦符合 回文串 ，那么当前子串一定是我们的预期答案（“之一”）
            // 因为我们 curMaxLength 在一次次遍历中在递减
            if (isValid(subStr)) {
                return subStr;
            }
        }
    }

    // 边界：可能 l为0 、然后直接到这里了，需要返回空字符串（不过题目 1 <= s.length <= 1000 ，故 可省略 ）
    return "";
}

2 方案2

1)代码：

// 方案2 动态规划，(s[i] === s[j] && dp[i + 1][j - 1]) || (s[i] === s[j] && ((j + 1) - i) < 3)
var longestPalindrome = function(s) {
    const l = s.length,
        // 1）含义：s[i][j] 表示s[i, j]是否为回文串（双闭区间）
        // 初始化1：dp， n*n 个值都初始化为 false 
        dp = new Array(l).fill(false).map(item => new Array(l).fill(false));
    // 当前 最长回文子串 的开始下标、最大长度
    let maxStartIndex = 0,
        // 边界：maxLength 初始化为1。不然会有问题、可自行思考~
        maxLength = 1;

    // 初始化2：dp对角线上值 均为 true 
    for (let i = 0; i < l; i++) {
        for(let j = 0; j < l; j++) {
            if (i === j) {
                dp[i][j] = true;
            }
        }
    }

    // 2）状态转移方程：
    // s[i][j] = (s[i] === s[j] && dp[i + 1][j - 1]) || (s[i] === s[j] && ((j + 1) - i) < 3)
    // s[i][j] = (当前首、尾字符相同 && 首、尾各往中间缩1位依旧是回文串) 
    // 或 (当前首、尾字符相同 && 当前首、尾位置间隔 < 3) 如 "bb" 这种长度小于3时，只要保证 首、尾字符相同即可
    for (let j = 1; j < l; j++) {
        for(let i = 0; i < j; i++) {
            if ((s[i] === s[j] && dp[i + 1][j - 1]) || (s[i] === s[j] && ((j + 1) - i) < 3)) {
                dp[i][j] = true;
                // 当前s[i, j]为回文串了，才看是否需要更新 maxStartIndex、maxLength 值
                // 3）当 s[i, j]为回文串 && (j + 1) - i) > maxLength 时，更新 maxStartIndex、maxLength 值
                if (((j + 1) - i) > maxLength) {
                    maxStartIndex = i;
                    maxLength = ((j + 1) - i);
                }
            } else {
                dp[i][j] = false;
            }
        }
    }

    // 最后根据 “我们所维护的” maxStartIndex, maxLength 得出相应的子串
    return s.substr(maxStartIndex, maxLength);
}

3 方案3

1)代码：

// 方案3 中心扩散法（注意“都进行奇、偶情况的处理”）
var longestPalindrome = function(s) {
    // 根据传入的子串、左 右边界下标，不断“向外”移动、试图拿到更长的回文串
    const helper = (str, left, right) => {
        while(left >=0 && right < l) {
            if (str[left] === str[right]) {
                // 看看是否需更新 maxStartIndex、maxLength 值
                if ((right + 1 - left) > maxLength) {
                    maxStartIndex = left;
                    maxLength = (right + 1 - left);
                }
                // 注意：这2语句放当前if分支的最后面、别放在最前面了！！
                // 继续“向外”移动、试图拿到更长的回文串
                left--;
                right++;
            } else {
                // 此时 str[left] !== str[right] ，肯定无法拿到更长的回文串，退出循环！
                break;
            }
        }
    }

    const l = s.length;
    // 当前“最长回文串”对应的 开始下标、最大长度。
    let maxStartIndex = 0,
        maxLength = 0;

    for (let i = 0 ; i < l; i++) {
        // 1）奇数：以 s[i] “向外”移动、试图拿到更长的回文串
        helper(s, i ,i);
        // 2）偶数：以 s[i]、s[i + 1] “向外”移动、试图拿到更长的回文串
        helper(s, i, i + 1);
    }
    
    return s.substr(maxStartIndex, maxLength);
}

4 方案4

1)代码：

// 方案4 Manacher（“马拉车”）算法
class Solution {
    public String longestPalindrome(String s) {
        int start = 0, end = -1;
        StringBuffer t = new StringBuffer("#");
        for (int i = 0; i < s.length(); ++i) {
            t.append(s.charAt(i));
            t.append('#');
        }
        t.append('#');
        s = t.toString();

        List<Integer> arm_len = new ArrayList<Integer>();
        int right = -1, j = -1;
        for (int i = 0; i < s.length(); ++i) {
            int cur_arm_len;
            if (right >= i) {
                int i_sym = j * 2 - i;
                int min_arm_len = Math.min(arm_len.get(i_sym), right - i);
                cur_arm_len = expand(s, i - min_arm_len, i + min_arm_len);
            } else {
                cur_arm_len = expand(s, i, i);
            }
            arm_len.add(cur_arm_len);
            if (i + cur_arm_len > right) {
                j = i;
                right = i + cur_arm_len;
            }
            if (cur_arm_len * 2 + 1 > end - start) {
                start = i - cur_arm_len;
                end = i + cur_arm_len;
            }
        }

        StringBuffer ans = new StringBuffer();
        for (int i = start; i <= end; ++i) {
            if (s.charAt(i) != '#') {
                ans.append(s.charAt(i));
            }
        }
        return ans.toString();
    }

    public int expand(String s, int left, int right) {
        while (left >= 0 && right < s.length() && s.charAt(left) == s.charAt(right)) {
            --left;
            ++right;
        }
        return (right - left - 2) / 2;
    }
}

四 更多

1 刷题进度

1）LeetCode：307 / 2390 。

2）《剑指offer》：66 / 66 。

3）相关学习资料与笔记汇总： https://github.com/CYBYOB/algorithm-leetcode/tree/master/资料%26笔记 。

4）注：所有题目均有 2-5种 左右的解法，后续还将不断更新题目 & 题解。
敬请期待~
也欢迎大家进群一起 学习、交流、刷题&拿高薪~

2 GitHub - LeetCode项目仓库

0）本项目地址： https://github.com/CYBYOB/algorithm-leetcode 。
目标、愿景：
让每个人都能拥有一定的算法能力、以应对面试中（会举一反三的同学还可以将其融入自己的肌肉和血液，甚至能够赋能于公司的业务和技术）的算法。

1）项目的根目录下的 README.md 文件，
可以帮您快速查阅每1道题的来源、难度、所有的题解方案等。

2）而每个题解（即 index.md 文件）中，
还将附带题目描述、所有的题解方案的思维导图（ .xmind 文件）、思路和技巧等。

3）每种题解方案都有详细的注释，
通过“数字步骤”将抽象的算法逻辑、
清晰和有层次的展示于您的面前。
可以说是，
开箱即用~

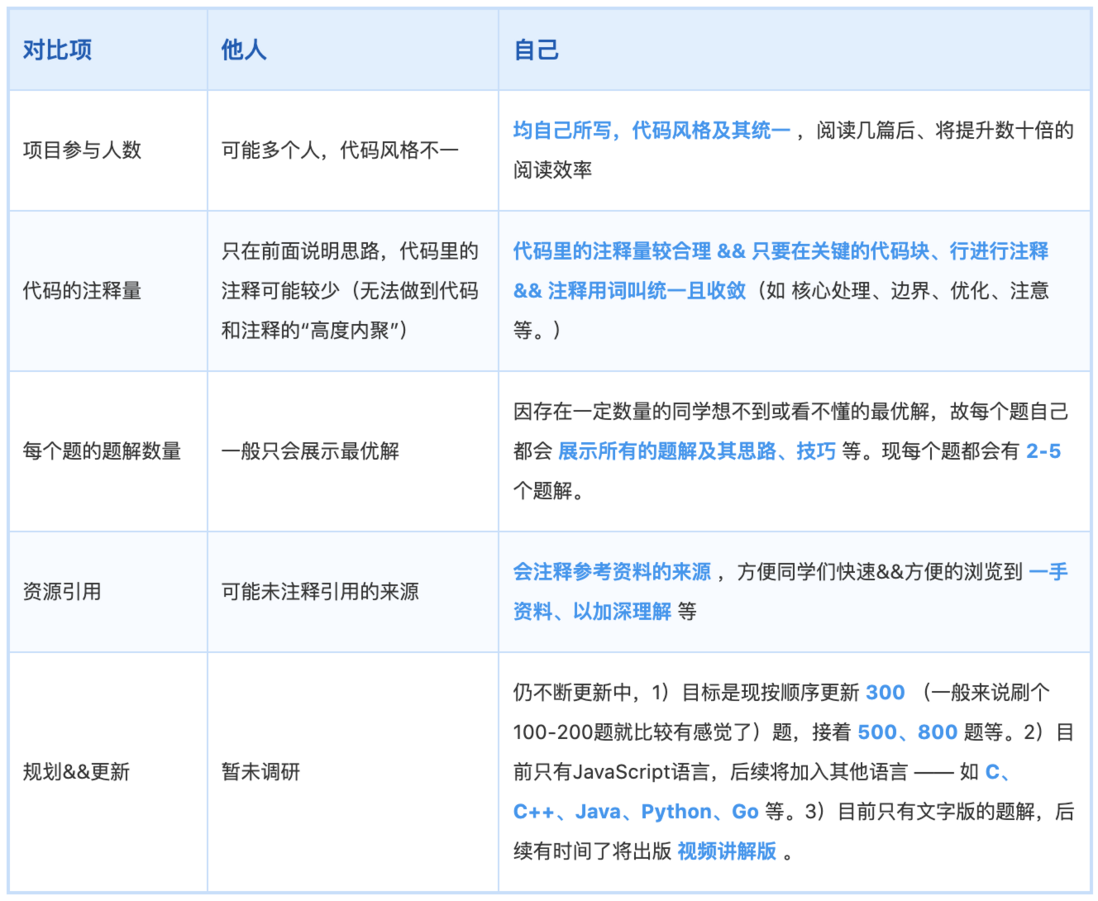
4）所有的题解方案都是经过作者1人之手，
故代码风格及其统一。
一旦阅读达到一定量后，
后续将大大提升您的阅读速度 —— “正所谓、量变引起质变”。

5）本人每周仍在不断的更新 —— 保证每周都有新的题目、题解方案刺激着您的神经 和 刷题欲望。
欢迎对算法感兴趣的同学加入我们的社群。
QQ群： 933919972 ；
作者QQ： 1520112971 ；
作者VX： c13227839870（可拉您进群、一起学习与交流~） 。

3 作者标签

1）“BAT里1名小小的伪全栈工程师，主攻前端，偶尔写点后端”。

2）2019年的微信小程序应用开发赛 - 全国三等奖；
2019CODA比赛 - 前 17/211 强 且 荣获“优秀团队”称号 等。

3）“半自媒体人”，
在校期间、个人公众号（IT三少。新自媒体（公众号）号： 码农三少 ）
在半年内实现了0到5.8K+的粉丝增长等。