JavaScript Math Curve-Archimedes Spiral

Introduction

When studying curve motion recently, after trying the SVG path exported by AI, I found that some of them are better to return to mathematics. I collected some information and summarized it after trying.

• Origin
• My GitHub

Introduction

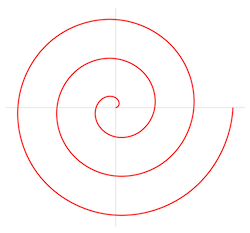
The Archimedes spiral is a spiral named after the Greek mathematician Archimedes in the 3rd century BC. It is a trajectory corresponding to the position of a point within a period of time, and the point leaves a fixed point at a constant speed along a line rotating at a constant angular speed. Formula description in polar coordinate system:

When c = 1, it is the so-called Archimedes spiral.
Formula description:

• r: Radial distance.
• a: Constant, the distance between the starting point and the center of polar coordinates.
• b: Constant, which controls the distance between two adjacent curves of the spiral.
• θ: Polar angle.
  Practical applications are:
• The Archimedes spiral can be found in a helical antenna, which can work in a wide frequency range.
• Asking patients to draw an Archimedes spiral is a way to quantify human tremor, and this information can help diagnose neurological diseases.
• Archimedes spirals are also used in digital light processing (DLP) projection systems to minimize the "rainbow effect", making it appear as if multiple colors are displayed at the same time, but actually due to the red, green, and blue cycle speedy.

• The Archimedes spiral is used in food microbiology to quantify bacterial concentration through a spiral disk.

  draw

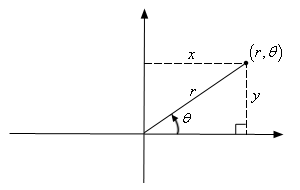
  Use canvas to draw a curve. The coordinate system of the canvas is a Cartesian coordinate system, which requires a conversion.
  
  From the above figure, it can be seen that taking a point has the following mathematical conversion relationship:

  x = rcos(θ)
  y = rsin(θ)
  θ = arctan(y/x)

  Combined with the formula of the polar coordinate system, we can get:

  x = (a + bθ)cos(θ)
  y = (a + bθ)sin(θ)

  This is the example , drawing the main logic code:

  function draw() {
  let a = 0, b = 10, angle = 0;
  let x = 0, y = 0, points = [];
  const acceleration = 0.1, circleNum = 2;
  // 注意这里角度的递增，以 2 * Math.PI 为基准进行比较，控制画多少圈
  while (angle <= circleNum * 2 * Math.PI) {
    x = (a + b * angle) * Math.cos(angle);
    y = (a + b * angle) * Math.sin(angle);
    points.push([x, y]);
    angle = angle + acceleration;
  }
  // 实现把点绘制成线的方法
  line({ points: points});
  }

  Changing the parameters will produce many different graphs, some of which do not look like curves.

  Reference

• Archimedean spiral Wiki
• Archimedean spiral Wolfram MathWorld
• Archimedean Spiral Plane Curves
• spiral