引子
继阿基米德螺线之后,发现等角螺线。
简介
等角螺线又称为黄金螺线或对数螺线,1638 年 Descartes 发现了等角螺线,后来 Jakob Bernoulli 研究发现了等角螺线自再造的特性,Jakob Bernoulli 对螺线非常着迷,以至于他要求刻在自己的墓碑上,并附词 “eadem mutata resurgo”(“纵使改变,依然故我”)。最后,Torricelli 独立完成了这项工作,并找到了曲线的长度。
等角螺线名称的由来,由于其特性:在螺线上任取一点 A ,该点与极坐标极点相连形成的直线,与该点的切线形成的夹角为定值。
在极坐标系中公式描述:
公式说明:
- r :与原点的距离。
- a :常数。
- b :常数。
- e :常数。
- θ :与 x 轴的角度。
自然现象有:
- 鹦鹉螺的贝壳像等角螺线。
- 菊的种子排列成等角螺线。
- 昆虫以等角螺线的方式接近光源。
- 旋涡星系的旋臂差不多是等角螺线。
- 低气压(热带气旋、温带气旋等)的外观像等角螺线
绘制
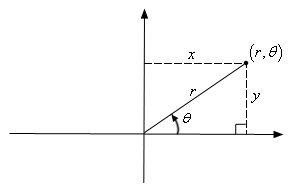
用 canvas 绘制曲线,canvas 的坐标系是笛卡尔坐标系,需要做一个转换。
由上面的图可知取一个点有下面的数学转换关系:
x = rcos(θ)
y = rsin(θ)
θ = arctan(y/x)结合极坐标系的公式可得:
这是示例,绘制主要逻辑代码:
function draw() {
let a = 0.1, b = 0.3, angle = 0;
let x = 0, y = 0, points = [];
const acceleration = 0.1, circleNum = 4;
// 注意这里角度的递增,以 2 * Math.PI 为基准进行比较,控制画多少圈
while (angle <= circleNum * 2 * Math.PI) {
const anglePow = Math.pow(Math.E, b * angle);
x = a * anglePow * Math.cos(angle);
y = a * anglePow * Math.sin(angle);
points.push([x, y]);
angle = angle + acceleration;
}
// 实现把点绘制成线的方法
line({ points: points});
}


**粗体** _斜体_ [链接](http://example.com) `代码` - 列表 > 引用。你还可以使用@来通知其他用户。