集合
成一个既没有重复元素,也没有顺序概念的数组。用对象{}表示。
function Set(){
var items={};
//向集合添加一个新的项。true,表示添加了这个值。如果集合中已经有这个值,就返回false,表示没有添加它。
this.add=function(value){
if(!this.has(value)){
items[value]=value;
return true;
}
return false;
}
//从集合移除一个值。
this.remove=function(value){
if(items[value]){
delete items[value];
return true;
}
return false;
}
//如果值在集合中,返回true,否则返回false。
this.has=function(value){
return return items.hasOwnProperty(value);
}
//移除集合中的所有项。
this.clear=function(){
items={};
}
//返回集合所包含元素的数量。与数组的length属性类似。
this.size=function(){
return Object.keys(items).length;
}
//返回一个包含集合中所有值的数组。
this.values=function(){
return Object.keys(items);
}
}并集
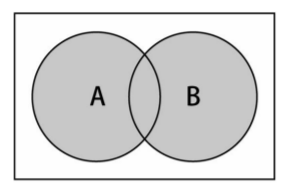
对于给定的两个集合,返回一个包含两个集合中所有元素的新集合。Object.assign(),2个都要;
并集的数学概念,集合A和B的并集,表示为A∪B,定义如下:A∪B = { x | x ∈ A∨x ∈ B }
意思是x(元素)存在于A中,或x存在于B中。
现在来实现Set类的union方法:
this.union = function(otherSet){
var unionSet = new Set();
var values = this.values();
for (var i=0; i<values.length; i++){
unionSet.add(values[i]);
}
values = otherSet.values();
for (var i=0; i<values.length; i++){
unionSet.add(values[i]);
}
return unionSet;
}; 测试一下上面的代码:
var setA = new Set();
setA.add(1);
setA.add(2);
setA.add(3);
var setB = new Set();
setB.add(3);
setB.add(4);
setB.add(5);
setB.add(6);
var unionAB = setA.union(setB);
console.log(unionAB.values());输出为["1", "2", "3", "4", "5", "6"]。注意元素3同时存在于A和B中,它在结果的集合中只出现一次。
交集
对于给定的两个集合,返回一个包含两个集合中共有元素的新集合。只要同时拥有的。
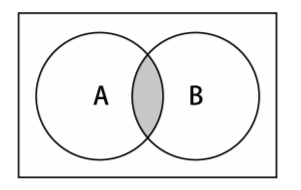
交集的数学概念,集合A和B的交集,表示为A∩B,定义如下:A∩B = { x | x ∈ A∧x ∈ B }
意思是x(元素)存在于A中,且x存在于B中。
现在来实现Set类的intersection方法:
this.intersection = function(otherSet){
var intersectionSet = new Set(); //同时都包含的
var values = this.values();
for (var i=0; i<values.length; i++){
if (otherSet.has(values[i])){
intersectionSet.add(values[i]);
}
}
return intersectionSet;
} 差集
对于给定的两个集合,返回一个包含所有存在于第一个集合且不存在于第二个集
合的元素的新集合。只要跟其它不相同的。
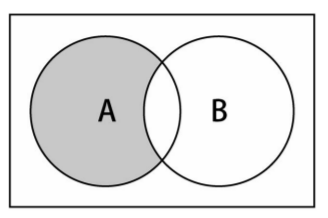
差集的数学概念,集合A和B的差集,表示为A-B,定义如下:A-B = { x | x ∈ A ∧ x B }
意思是x(元素)存在于A中,且x不存在于B中。
现在来实现Set类的difference方法:
this.difference = function(otherSet){
var differenceSet = new Set();//存在A不存在B,同样数据a.length>b.length 才会有值,[1,2,3,4]-[1,2,3]=4;
var values = this.values();
for (var i=0; i<values.length; i++){
if (!otherSet.has(values[i])){
differenceSet.add(values[i]);
}
}
return differenceSet;
};子集
验证一个给定集合是否是另一集合的子集。判断子集中一定都是父集中的。
子集的数学概念,集合A是B的子集(或集合B包含
了A),表示为A⊆B,定义如下:∀x { x ∈ A → x ∈ B }
意思是集合A中的每一个x(元素),也需要存在于B中。
现在来实现Set类的subset方法:
this.subset = function(otherSet){
if (this.size() > otherSet.size()){
return false;
} else {
var values = this.values();
for (var i=0; i<values.length; i++){
if (!otherSet.has(values[i])){
return false;
}
}
return true;
}
}; 字典
集合、字典和散列表可以存储不重复的值。在字典中,存储的是[键,值]
对,其中键名是用来查询特定元素的。字典也称作映射。
function Dictionary(){
var items={};
this.set=function(key,value){
items[key]=value;
}
this.remove=function(key){
if(this.has(key)){
delete items[key];
return true;
}
return false;
}
this.has=function(key){
return key in items;
}
this.get=function(key){
return this.has(key)?items[key]:undefined;
}
this.clear=function(){
items={};
}
this.size=function(){
return Object.keys(items).length;
}
this.keys=function(){
return Object.keys(items);
}
this.values=function(){
let values=[];
for(let key in items){
if(this.has(key)){
values.push(items[key])
}
}
return values;
}
this.getItems = function() {
return items;
}
}散列表
HashTable类,也叫HashMap类,是Dictionary类的一种散列表实
现方式。使用数组方式。
散列算法的作用是尽可能快地在数据结构中找到一个值。道如果
要在数据结构中获得一个值(使用get方法),需要遍历整个数据结构来找到它。如果使用散列
函数,就知道值的具体位置,因此能够快速检索到该值。散列函数的作用是给定一个键值,然后返回值在表中的地址。
先实现一个散列函数是HashTable类的私有方法,获得将每个键值中的每个字母的ASCII值和一个数字。
let loseloseHashCode=function(key){
let hash=5381;
for(let i=0;i<key.length;i++){
hase=hash*33+key.charCodeAt(i);
}
return hash%1013;//1013是任意的质数,让值不要那么大
}`function HashTable(){
let table=[];
this.put=function(key,value){
let position=loseloseHashCode(key);
table[position]=value;
}
this.remove=function(key){
table[loseloseHashCode(key)]=undefined;
}
this.get=function(key){
return table[loseloseHashCode(key)]
}}`
树
非顺序数据结构——树,它对于存储需要快速查找的数据非常有用。
一个树结构包含一系列存在父子关系的节点。每个节点都有一个父节点(除了顶部的第一个
节点)以及零个或多个子节点:
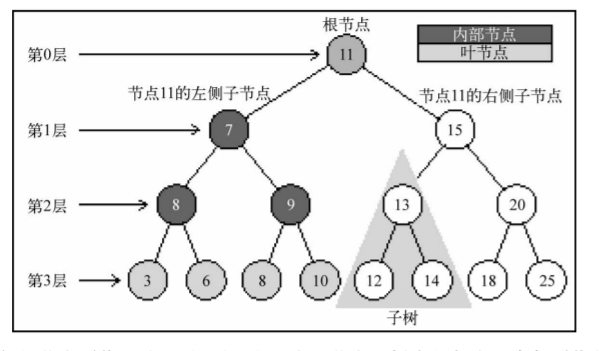
位于树顶部的节点叫作根节点(11)。它没有父节点。树中的每个元素都叫作节点,节点分
为内部节点和外部节点。至少有一个子节点的节点称为内部节点(7、5、9、15、13和20是内部
节点)。没有子元素的节点称为外部节点或叶节点(3、6、8、10、12、14、18和25是叶节点)。
一个节点可以有祖先和后代。一个节点(除了根节点)的祖先包括父节点、祖父节点、曾祖
父节点等。一个节点的后代包括子节点、孙子节点、曾孙节点等。例如,节点5的祖先有节点7
和节点11,后代有节点3和节点6
二叉树
二叉树中的节点最多只能有两个子节点:一个是左侧子节点,另一个是右侧子节点。这些定
义有助于我们写出更高效的向/从树中插入、查找和删除节点的算法。二叉树在计算机科学中的
应用非常广泛。
二叉搜索树(BST)是二叉树的一种,但是它只允许你在左侧节点存储(比父节点)小的值,
在右侧节点存储(比父节点)大(或者等于)的值。;
let insertNode=function(node,newNode){
//小了就在左边下级有了就找下下级,右边同理
if(newNode.key<node.key){
if(node.left===null){
node.left=newNode;
}else{
insertNode(node.left,newNode)
}
}else{
if(node.right===null){
node.right=newNode;
}else{
insertNode(node.right,newNode);
}
}
}function BinarySearchTree(){
let Node=function(key){
this.key=key;
this.left=null;
this.right=null;
}
let root=null;
this.insert=function(key){
let newNode=new Node(key);
if(root===null){
root=newNode;
}else{
insertNode(root,newNode);
}
}
this.search=function(key){
}
this.inOrderTraverse=function(callback){}
this.preOrderTraverse=function(){}
this.postOrderTraverse=function(){}
this.min=function(){}
this.max=function(){}
this.remove=function(key){
}
}中序遍历
中序遍历是一种以上行顺序访问BST所有节点的遍历方式,也就是以从最小到最大的顺序访
问所有节点。中序遍历的一种应用就是对树进行排序操作。
首先要检查以参数形式传入的节点是否为null(这就
是停止递归继续执行的判断条件——递归算法的基本条件)。
然后,递归调用相同的函数来访问左侧子节点。接着对这个节点进行一些操作
(callback),然后再访问右侧子节点
this.inOrderTraverse=function(callback){
inOrderTraverse(root,callback);
}let inOrderTraverseNode=function(node,callback){
if(node!==null){
inOrderTraverseNode(node.left,callback);
callback(node.key);
inOrderTraverseNode(node.right,callback);
}
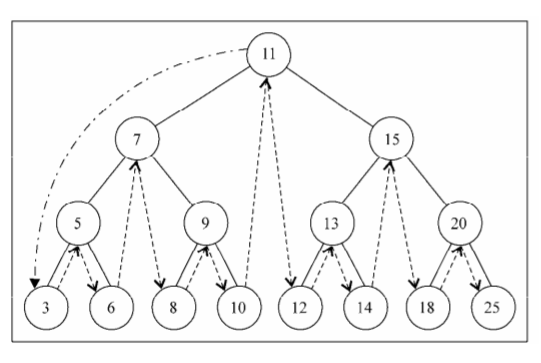
}inOrderTraverse方法的访问路径:
先序遍历
先序遍历是以优先于后代节点的顺序访问每个节点的。先序遍历的一种应用是打印一个结构
化的文档。
先序遍历和中序遍历的不同点是,先序遍历会先访问节点本身,然后再访问它的
左侧子节点,最后是右侧子节点。
this.preOrderTraverse=function(callback){
preOrderTraverseNode(root,callback)
}let preOrderTraverseNode=function(node,callback){
if(node!==null){
callback(node.key);
preOrderTraverseNode(node.left,callback);
preOrderTraverseNode(node.right,callbak);
}
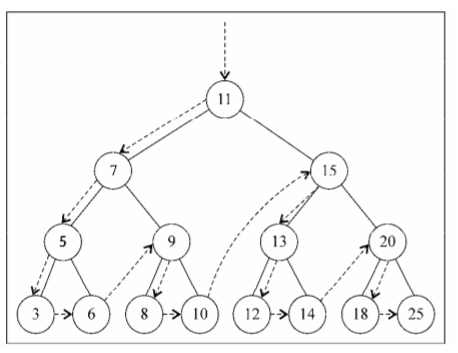
}preOrderTraverse方法的访问路径:
后序遍历
后序遍历则是先访问节点的后代节点,再访问节点本身。后序遍历的一种应用是计算一个目
录和它的子目录中所有文件所占空间的大小。
后序遍历会先访问左侧子节点,然后是右侧子节点,最后
是父节点本身
this.postOrderTraverse=function(callback){
postOrderTraverseNode(root,callback);
}let postOrderTraverseNode=function(node,callback){
if(node!==null){
postOrderTraverseNode(node.left,callback);
postOrderTraverseNode(node.right,callback);
callback(node.key);
}
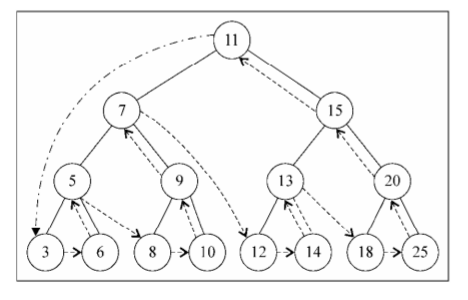
}postOrderTraverse方法的访问路径:
搜索最大最小值
小的在左边,大的在右边
this.min=function(){
return minNode(root);
}
let minNode=function(node){
if(node){
while(node&&node.left!==null){
node=node.left;
}
return node.key;
}
return null;
}this.max=function(){
return maxNode(root);
}
let maxNode=function(node){
if(node){
while(node&&node.right!==null){
node=node.right;
}
return node.key;
}
return null;
}搜索特定值
返回boolean;
this.search=function(key){
return searchNode(root,key);
}
let searchNode=function(node,key){
if(node===null){
return false;
}
if(key<node.key){
return searchNode(node.left,key);
}else if(key>node.key){
return searchNode(node.right,key);
}else{
return true;
}
}移除一个节点
this.remove=function(key){
root=removeNode(root,key);
}
let removeNode=function(node,key){
if(node===null){
return null;
}
if(key<node.key){
node.left=removeNode(node.left,key);
return node;
}else if(key>node.key){
node.right=removeNode(node.right,key);
return node;
}else{//找到了要找的,键=node.key
//第一种情况,一个叶节点
if(node.left===null&&node.right===null){
node=null;//移除此节点
return node;//使父节点指向子节点的指针指向null
}
//第二种情况,一个只有一个子节点的节点
if(node.left==null){
node=node.right;//把它下面的取代了它的位置,它就变没了删除了
return node;
}else if(node.right===null){
node=node.left;
return node;
}
//第三种情况,一个有2个子节点的节点,从右侧子树中找到最小的替换到它的位置,移除它
let aux=findMinNode(node.right);//找到右边最小的节点,跟min实现一样,但返回的是节点
node.key=aux.key;
node.right=removeNode(node.right,aux.key);//右侧最小的节点的右侧指向要删除的右侧节点
return node;
}
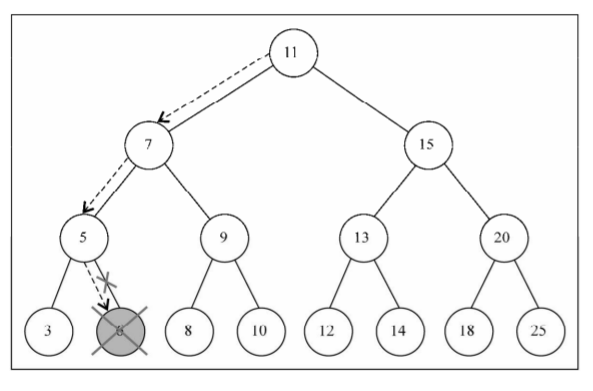
}移除一个叶节点:
移除一个有左侧或右侧节点的节点:
移除有2个节点的节点:
图
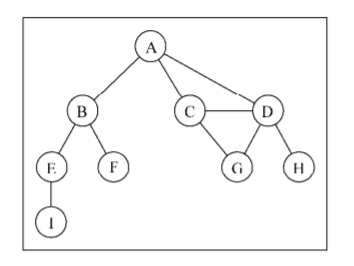
图是网络结构的抽象模型。图是一组由边连接的节点(或顶点)。
一个图G = (V, E)由以下元素组成。
V:一组顶点
E:一组边,连接V中的顶点




**粗体** _斜体_ [链接](http://example.com) `代码` - 列表 > 引用。你还可以使用@来通知其他用户。