第一题
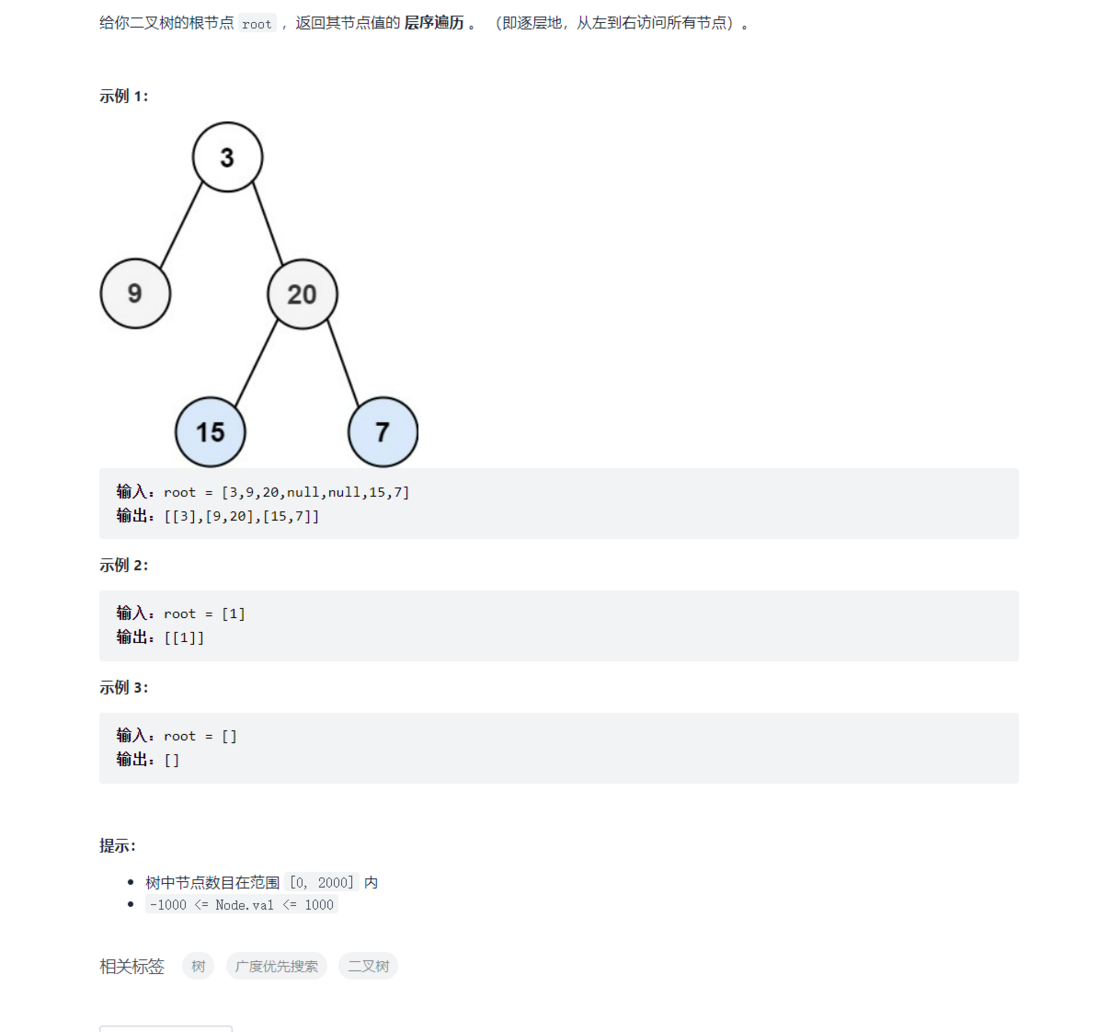
题目信息
解题思路
层序遍历二叉树,显然广搜更为高效
广搜的流程如图
因此我们需要拥有一个队列记录搜索的节点情况
我很抱歉
素朴的思路过于复杂
我并不能很好的把他展示出来
让我们学习优化一下解题思路
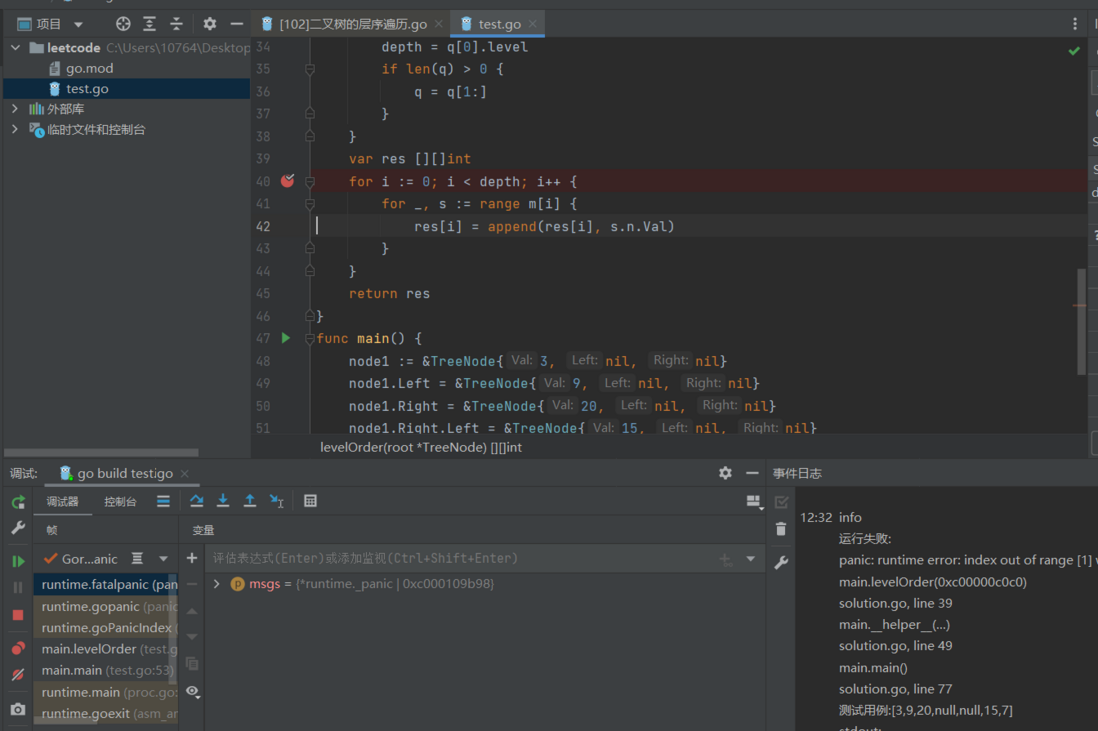
代码
func levelOrder(root *TreeNode) [][]int {
ret := [][]int{}
if root == nil {
return ret
}
q := []*TreeNode{root}
for i := 0; len(q) > 0; i++ {
ret = append(ret, []int{})
p := []*TreeNode{}
for j := 0; j < len(q); j++ {
node := q[j]
ret[i] = append(ret[i], node.Val)
if node.Left != nil {
p = append(p, node.Left)
}
if node.Right != nil {
p = append(p, node.Right)
}
}
q = p
}
return ret
}
作者:LeetCode-Solution
链接:https://leetcode-cn.com/problems/binary-tree-level-order-traversal/solution/er-cha-shu-de-ceng-xu-bian-li-by-leetcode-solution/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。复杂度分析
时间复杂度:每个点进队出队各一次,故渐进时间复杂度为 O(n)。
空间复杂度:队列中元素的个数不超过 n 个,故渐进空间复杂度为 O(n)。
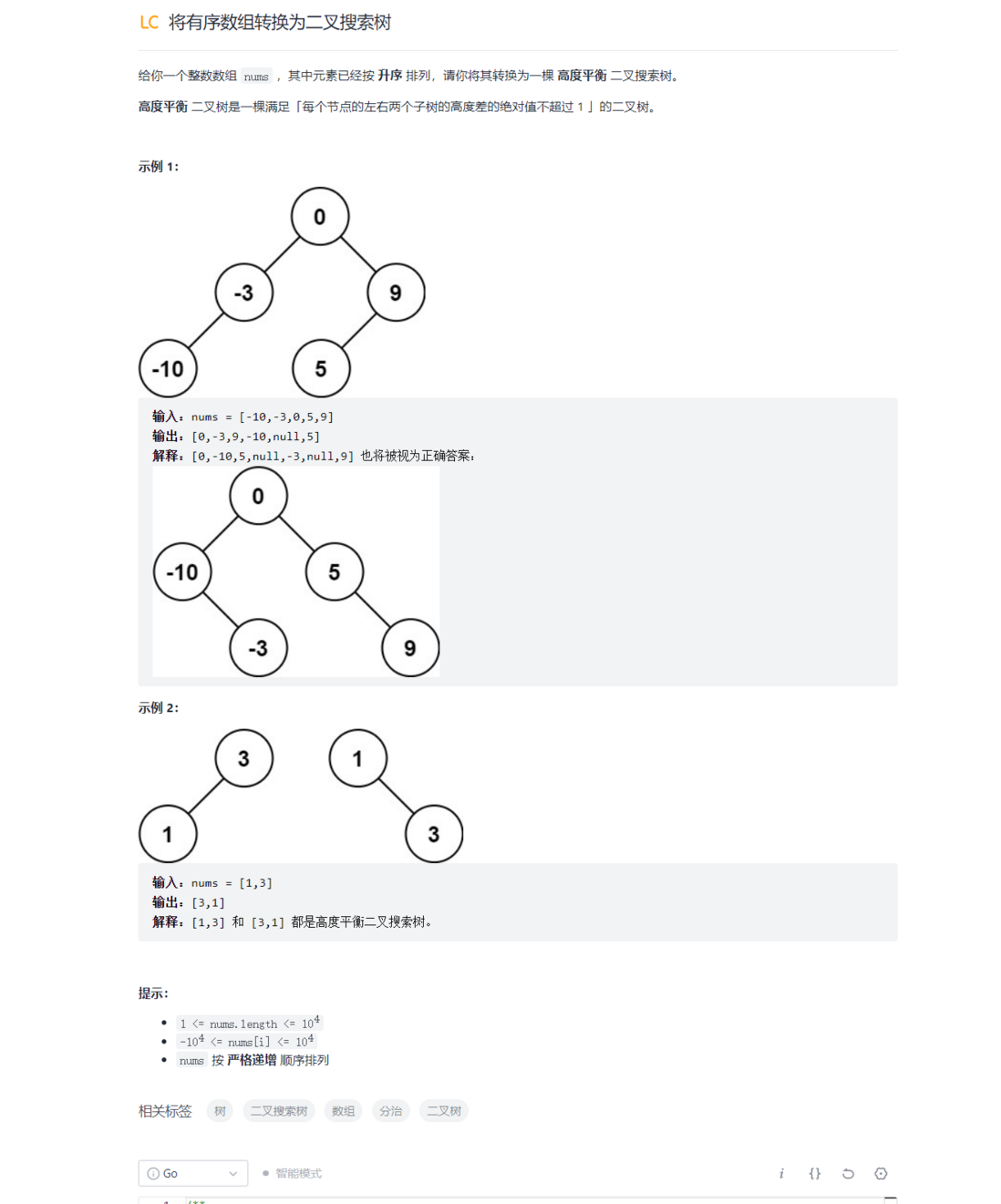
第二题 将有序数组转化为二叉搜索树
题目信息
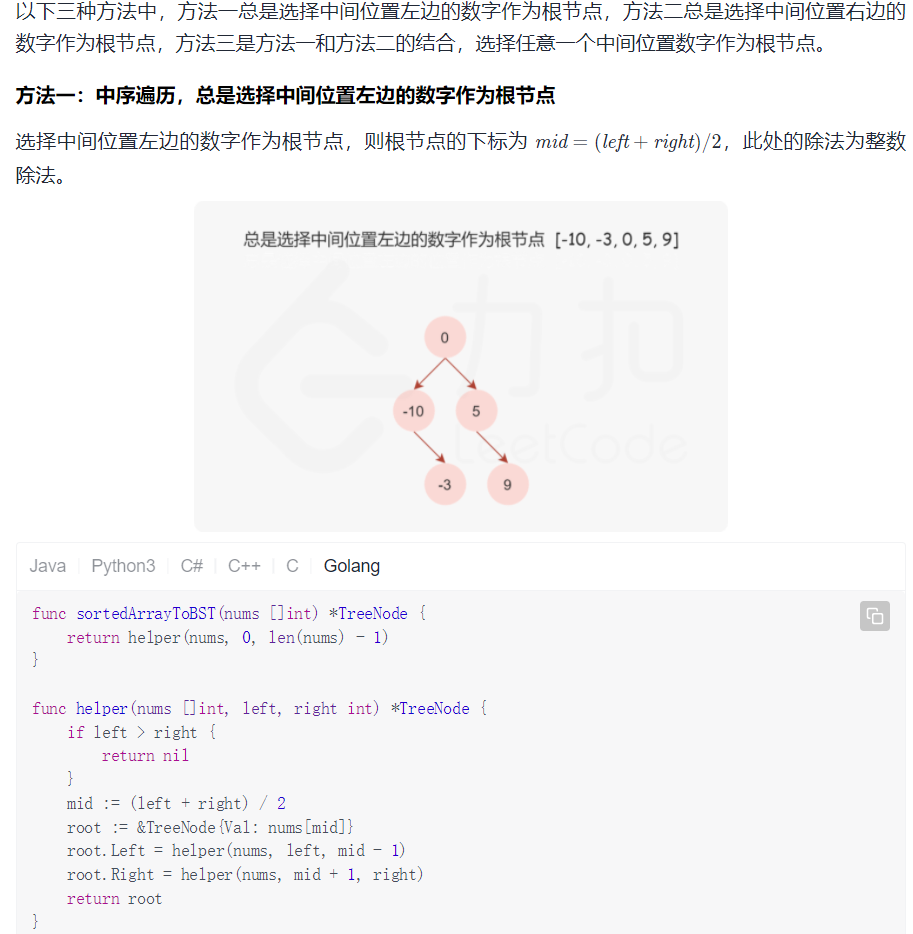
解题思路
代码
func sortedArrayToBST(nums []int) *TreeNode {
return helper(nums, 0, len(nums) - 1)
}
func helper(nums []int, left, right int) *TreeNode {
if left > right {
return nil
}
mid := (left + right) / 2
root := &TreeNode{Val: nums[mid]}
root.Left = helper(nums, left, mid - 1)
root.Right = helper(nums, mid + 1, right)
return root
}
作者:LeetCode-Solution
链接:https://leetcode-cn.com/problems/convert-sorted-array-to-binary-search-tree/solution/jiang-you-xu-shu-zu-zhuan-huan-wei-er-cha-sou-s-33/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。复杂度分析
时间复杂度:O(n),其中 n 是数组的长度。每个数字只访问一次。
空间复杂度:O(logn),其中 nn 是数组的长度。空间复杂度不考虑返回值,因此空间复杂度主要取决于递归栈的深度,递归栈的深度是 O(logn)。








**粗体** _斜体_ [链接](http://example.com) `代码` - 列表 > 引用。你还可以使用@来通知其他用户。