Leetcode 题解系列 -- 和为s的连续正数序列（滑动窗口）

休了个不短不长的年假，题解系列继续开工~

本专题旨在分享刷Leecode过程发现的一些思路有趣或者有价值的题目。

题目相关

• 原题地址: https://leetcode-cn.com/problems/he-wei-sde-lian-xu-zheng-shu-xu-lie-lcof/]

• 题目描述：

  输入一个正整数 target ，输出所有和为 target 的连续正整数序列（至少含有两个数）。序列内的数字由小到大排列，不同序列按照首个数字从小到大排列。

  • 示例 1：
    输入：target = 9
    输出：[[2,3,4],[4,5]]
  • 示例 2：
    输入：target = 15
    输出：[[1,2,3,4,5],[4,5,6],[7,8]]
    限制：1 <= target <= 10^5

思路解析

暴力破解

题目的含义比较清晰，需要求出和为特定值的 连续正整数序列。

首先，这道题的很直接的也会想到一个 -- 暴力破解:

具体思路：

• 首先寻找是否存在满足要求的，以1为开头的序列，所以初始化一个序列为 [ 1 ]

• 依次往序列里添加连续的正整数，让序列变成 [1, 2, 3..i. target]， 并且每次添加完一个整数时，对比当前序列所有整数之和sum，与目标值target的关系：

  • 如果sum < target，则继续往序列里添加下一个数；
  • 如果已经满足sum = target，那么存储当前序列，并且说明以1开始的序列寻找可以停止了；
  • 如果直接到sum > target，那么说明以1开始的序列寻找可以停止了（不存在以1为开头并且满足要求的序列）；
• 重复上述步骤，分别寻找以2，3, ... target开头且满足题意的序列；

上面这种思路的话 最坏的情况下，需要外层循环（外层循环也就是遍历以1..n开头的序列）n次，内层循环n次（内层循环就是寻找当前开头固定时，不同结尾的序列），那么总的复杂度就是O(n^2)，由于 1 <= target <= 10^5 , 所以O(n^2)明显超时;

红色区域表示序列，它的左边界和右边界有个特点，都只向右侧移动，而整个遍历的过程，其实就像是一个推拉窗的移动过程，这个算法也就由此得名。

滑动窗口

从上述过程可以看到，暴力破解的问题在于时间复杂度太高，而之所以高，是因为在遍历过程存在一些可以跳过的过程, 为了便于理解，我们带入一个题设中的示例1，target = 9的情况来进行演示。按照暴力破解思路：

• 首先序列为 [1] , 序列之和 sum = 1 , 1 < 9 继续循环;
• 序列为 [1, 2] , 序列之和 sum = 3 , 3 < 9 继续循环;
• 序列为 [1, 2，3] , 序列之和 sum = 6 , 6 < 9 继续循环;
• 序列为 [1, 2, 3 ,4] , 序列之和 sum = 12 , 12 > 9 ,那 Stop!;
  到此说明不存在以1为开头切满足要求的序列，那么按照前面的思路，接下来是要寻找以2开头且满足题意的序列，那么现在问题来了：

我们真的有必要从[2]开始吗？ 在找以1开头的序列时，我们已经发现[1,2,3]之和都小于target了，那序列[2,3]之和肯定也小于9，那为什么还要按部就班的，先走一次[2]再到[2,3] 再到[2,3,4]呢？

这，就是突破的关键！

所以我们发现，再找完以i开头的序列之后，跳到寻找以i+1开头的序列时，是可以跳过一些中间遍历次数的，可以这么做:

• 序列为 [1, 2, 3 ,4] , 序列之和 sum = 12， 12 < 9 ，此时要停止寻找以1为开头的序列，那么我们直接去掉序列左边的值，从[2,3,4]开始寻找以2开头的序列；
• 按照规则，[2, 3 ,4] 之和刚好为9，此时保存当前序列结果，并且停止寻找以2为开头切满足要求的序列，接下来准备寻找3开头的序列，我们同样去掉此时序列的最左边值, 从[3, 4]开始运算；

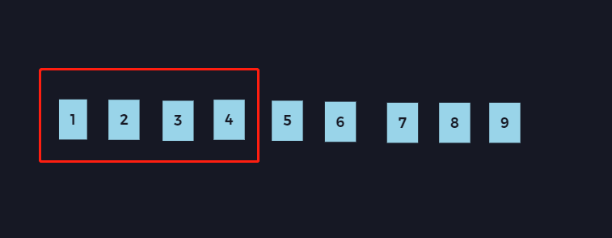
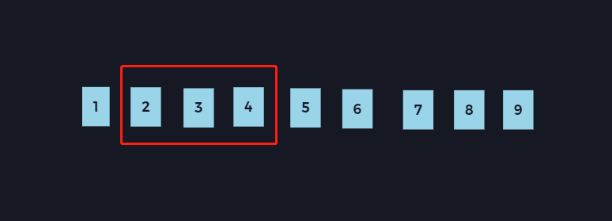
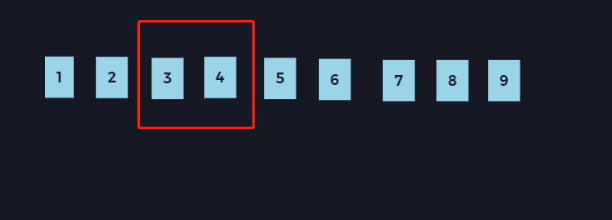
重复上述过程， 会发现，在遍历过程中，我们的序列如下图所示（懒得做动图了，分开看更有利于理解）:

红色区域表示序列，它的左边界和右边界有个特点，都只向右侧移动，而整个遍历的过程，其实就像是一个推拉窗的移动过程，这个算法也就由此得名。

当然，要使用上面的算法，我们要回答一个问题：相较于暴力破解，滑动窗口确实减少了循环次数，但是滑动窗口能否找到所有的解呢？（也就是在上述的跳跃过程导致遗漏呢？）

这个是可以证明的，因为按照前文的遍历思路：

• 寻找1开头的序列时，只要序列之和小于target，则窗口右边界一直往右拓展，直到找到[1,2,3]时，此时序列值之和还是小于target; 而到[1,2,3,4]时，此时序列之和第一次大于target，说明以1开头的序列寻找结束;
• 那么此时以2开头的序列 [2,3] < [1,2,3] < target， 说明只需要从[2,3,4]开始寻找就可以了，（读者朋友也可以拿示例2带入试试看，加深理解）以此类推，说明滑动窗口的算法是不会有遗漏的。

完整代码

到这里只需要整理前面的思路，伪代码也就出来了：

• 初始化，设定序列窗口的左右边界，分别为 1,2 ，然后开始循环；
• 循环，当序列内之和小于target时，右边界右移；
• 循环过程如果发现序列值和等于target，则存储当前序列，并且把左边界右移；
• 循环过程如果发现序列值和大于target，则把左边界右移；
• 当左边界追上右边界时，循环结束（可以思考下为什么？）

那么实际代码如下：

var findContinuousSequence = function(target) {
  const res = [];
  const sum = [0, 1];
  let l = 1; // 左边界
  let r = 2; // 右边界
  let s = 3; // 当前序列之和sum
  while(l < r){
      if(s === target) {
          // 满足题意的序列添加到结果
          res.push(getList(l, r));
      }

      if(s > target) {
          s = s - l;
          l++;
      } else {
          r++;
          s += r; 
      }
  }
  return res;
};

function getList (l, r) {
  const res = [];
  for(let i = l; i<=r; i++) {
      res.push(i)
  }
  return res;
}

那么滑动窗口的内容就到此为止了~

此外...

在文章末尾顺便打个小广告，问下有没有想来外企955的小伙伴：

• 面朝大海办公，不打卡 不考勤 到点就下班，工作生活两不误；
• 假期超长（每年年假+带薪病假+企业年假 = 20天起步！）；
• 而且很多岗位可以长期远程办公！ 不再困扰与一线高昂房价难落地的问题；
• 可内推，base杭州和厦门~