【golang】leetcode中级-在排序数组中查找元素的第一个和最后一个位置&合并区间

第一题 在排序数组中查找元素的第一个和最后一个位置

题目

错误案例

func searchRange(nums []int, target int) []int {
    res:=make([]int,2)
    n:=len(nums)
    if n==1{
        if nums[0]==target{
            return res
        }else{
            res[0]=-1
            res[1]=-1
            return res
        }
    }
    mid:=n/2
    s1:=searchRange(nums[:mid],target)
    s2:=searchRange(nums[mid:], target)

    if s1[0]==-1&&s2[0]==-1{
        res[0]=-1
        res[1]=-1
        return res
    }
    if s1[0]==-1{
        res[0]=s2[0]+mid
        res[1]=s2[1]+mid
    }else if s2[0]==-1{
        res[0]=s1[0]
        res[1]=s1[1]
    }else{
        res[0]=s1[0]
        res[1]=s2[1]+mid
    }
    return res
}

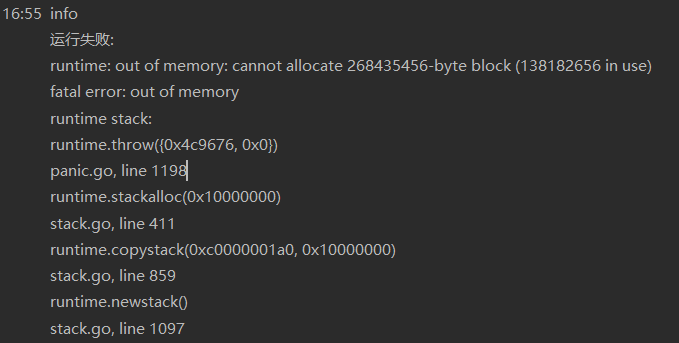
结果

....

原因是因为

正确解法

使用sort.SearchInts函数

func searchRange(nums []int, target int) []int {
    leftmost := sort.SearchInts(nums, target)
    if leftmost == len(nums) || nums[leftmost] != target {
        return []int{-1, -1}
    }
    rightmost := sort.SearchInts(nums, target + 1) - 1
    return []int{leftmost, rightmost}
}

作者：LeetCode-Solution
链接：https://leetcode-cn.com/problems/find-first-and-last-position-of-element-in-sorted-array/solution/zai-pai-xu-shu-zu-zhong-cha-zhao-yuan-su-de-di-3-4/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

解析

https://blog.csdn.net/luyuan4...

复杂度分析

时间复杂度：O(logn) ，其中 n 为数组的长度。二分查找的时间复杂度为 O(logn)，一共会执行两次，因此总时间复杂度为 O(logn)。

空间复杂度：O(1) 。只需要常数空间存放若干变量。

第二题 合并区间

题目

解题思路

代码

func merge(intervals [][]int) [][]int {
    //先从小到大排序
    sort.Slice(intervals,func(i,j int)bool{
        return intervals[i][0]<intervals[j][0]
    })
    //再弄重复的
    for i:=0;i<len(intervals)-1;i++{
        if intervals[i][1]>=intervals[i+1][0]{//区间左端与上一个区间有交集，可以并入
            intervals[i][1]=max(intervals[i][1],intervals[i+1][1])//赋值最大值
            intervals=append(intervals[:i+1],intervals[i+2:]...)//覆盖i+1
            i--
        }
    }
    return intervals
}
func max(a,b int)int{
    if a>b{
        return a
    }
    return b
}

复杂度分析

时间复杂度：O(nlogn)，其中 n 为区间的数量。除去排序的开销，我们只需要一次线性扫描，所以主要的时间开销是排序的 O(nlogn)。

空间复杂度：O(logn)，其中 n 为区间的数量。这里计算的是存储答案之外，使用的额外空间。O(logn) 即为排序所需要的空间复杂度。