【golang】leetcode中级-跳跃游戏&不同路径

第一题 跳跃游戏

题目

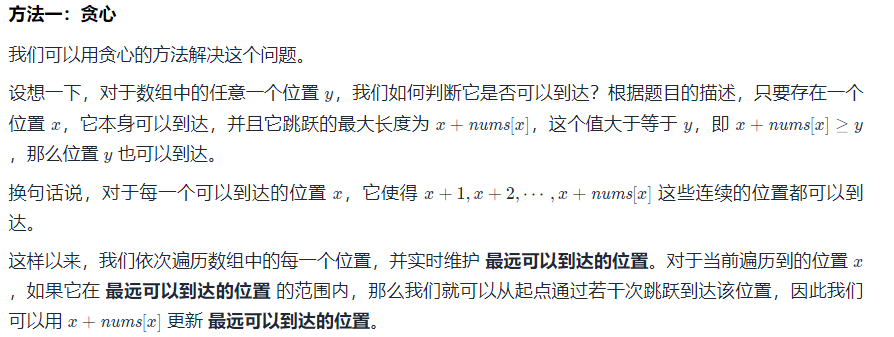
贪心解法

对于每个下标而言，元素规定了它可以到达的最大距离

因此这部分距离范围内的下标都是可以抵达的
.

例如示例1：nums = [2,3,1,1,4]
.

对于下标0而言，它可以选择下标1或者下标2

选择下标1.可以到达下标4

选择下标2，可以到达下标3

.

由于本题返回值为布尔类型，无需存储跳跃路径

我们只需记住跳跃能到达的最远下标即可，

对于最远下标以内，我们总能找到一条可以抵达的路径

因此我们可以得到公式

maxIndex=max(maxIndex,i+nums[i])

直到最远下标抵达最后一个下标

if maxIndex>=n-1 {return true}

核心思想为 贪心算法 ，即优先考虑可获得的最佳的解法

对于每个下标，我们都将其最优解加入考虑范围

具体代码

func canJump(nums []int) bool {
    n:=len(nums)
    var maxIndex int
    for i:=0;i<n;i++{
        if i>maxIndex{return false}
        maxIndex=max(maxIndex,i+nums[i])
        if maxIndex>=n-1 {return true}
    }
    return false
}

func max(x int,y int)int {
    if x<y{
        return y
    }else {
        return x
    }
}

官解

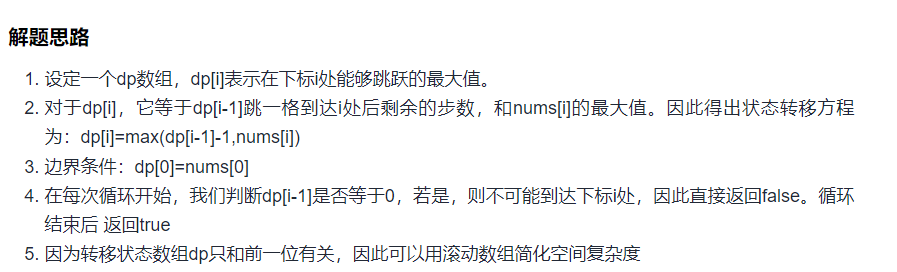
动态规划解法

在用动态规划求解之前，让我们在强调一下动态规划的几个步骤

详细学习可以参考
https://labuladong.gitee.io/a...

https://houbb.github.io/2020/...

而对于本题而言

代码

func canJump(nums []int) bool {

    n:=len(nums)
    a:=nums[0]  // a=dp[i-1]
    for i:=1;i<n;i++ {
        if a==0  {return false}
        a=max(a-1,nums[i])    // a=dp[i]
    }
    return true
}

func max(x int,y int)int {
    if x<y{
        return y
    }else {
        return x
    }
}

复杂度分析

时间复杂度：O(n)，其中 n 为数组的大小。只需要访问 nums 数组一遍，共 n 个位置。

空间复杂度：O(1) ，常数级的空间开销。

第二题 不同路径

题目

思路

dp

这是组合数学中经典的格路模型，它的计算与杨辉三角是等价的

都是

f(i,j)=f(i−1,j)+f(i,j−1)

代码

func uniquePaths(m int, n int) int {
    //初始化
    arr := make([][]int, m)
    for i := range arr {
        arr[i] = make([]int, n)
        arr[i][0]=1
    }
    for i:=range arr[0]{
        arr[0][i]=1
    }
    if m==1||n==1 {return 1}

    for i:=1;i<m;i++{
        for j:=1;j<n;j++{
            arr[i][j]=arr[i-1][j]+arr[i][j-1]
        }
    }
    return arr[m-1][n-1]
}

复杂度分析

时间复杂度：O（mn），计算了m*n矩阵个数值，最终得到第m行第n列的答案

空间复杂度：O（mn），借助二维数组得到最终答案

同时

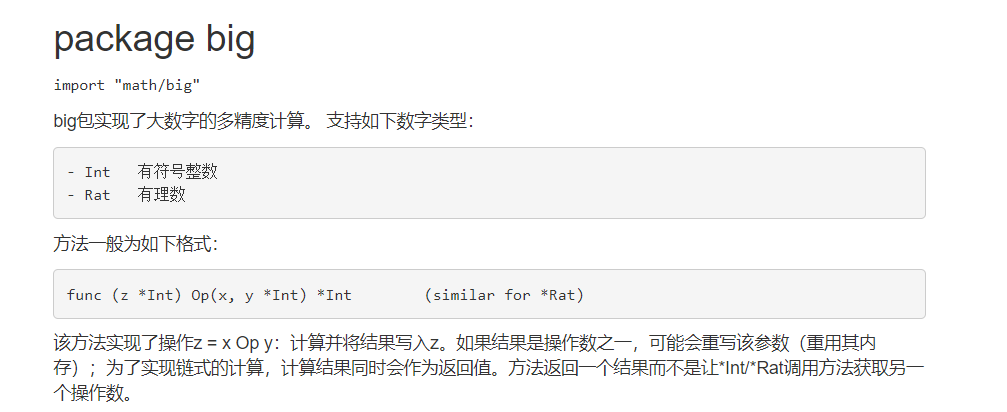
组合数学

go语言中提供了计算排列组合数的方法

因此我们也可以直接调用该方法获取答案

方法具体参数为

第m，n项的组合数为

故代码为

func uniquePaths(m, n int) int {
    return int(new(big.Int).Binomial(int64(m+n-2), int64(n-1)).Int64())
}