判断多边形是否属于复杂多边形

标注场景下，用户可以选取多点框选一个区域，这样会生成一个多边形。但某些多边形不适合标注场景，还会增加其他参数计算复杂度，需要判断出来禁止绘制。

分类

根据标注的场景，可以将多边形归纳为边有交点多边形与边无无交点多边形。如图：

这样实际上就是多边形划分中的简单多边形与复杂多边形。

我们可以通过多边形边之间是否有相交来判断。

判断

怎么判断变是否相交呢？

如果去计算交点是否落于连线上，不仅计算量大，而且还会因为比较精度等问题导致麻烦。这类问题早已有更好的方案：相交的线段的特征是端点分别位于相交的线段两侧，只需要判断两个端点是否在线段两侧就能判断线段是否能相交。

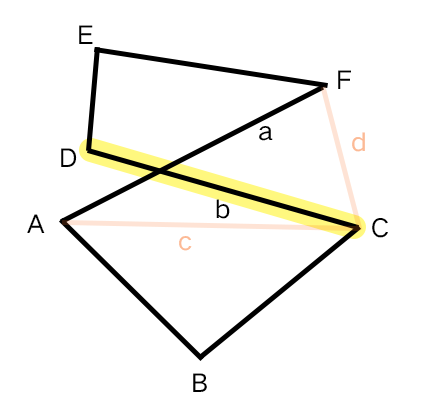
以右边复杂多边形举例：

\( 点_A,点_F \)组成的\( 线段a \)与\( 点_C,点_D \)组成的\( 线段b \)相交。\( 线段a \)的两个端点\( A \)、\( F \)必然在\( 线段b \)的两侧，反之亦然。

如何计算出端点在线段两侧呢？

可以利用数学工具向量的叉乘（Cross product）来简化几何运算，叉乘在二维计算上的结果是具有方向含义的。

我们只需选择一条线作为中线，将其端点与需要判断的端点连接做出新的线，然后辅助线与中线运算，如果符号相异则说明是在两侧，线段是可以相交的。

计算

二维叉乘的计算公式：

$$ a \times b = \begin{bmatrix} x_a & x_b \\ y_a & y_b \end{bmatrix} = x_a y_b - x_b y_a $$

已知图形的各个顶点坐标，比如\( 点_A \)坐标为\( (x_1,y_1) \)，并且顶点仅能顺序直线相连。

现在取\( b（点_C,点_D） \)作中线，取\( 点_C \)为起点，连接需要计算的\( 点_A,点_F \)，这时候我们有了一条中线，与两条新画的辅助线：

中线\( b（点_C,点_D） \)向量表示：\( V_b(x_c - x_d, y_c - y_d) = V_b(x_b, y_b) \)

辅助线\( c（点_C,点_A） \)向量表示：\( V_c(x_C - x_A, y_C - y_A) = V_c(x_c, y_c) \)

辅助线\( d（点_C,点_F） \)向量表示：\( V_d(x_C - x_F, y_C - y_F) = V_d(x_d, y_d) \)

计算\( V_b \times V_c = x_b \cdot y_c - x_c \cdot y_b \)可得出正负，由此可知\( 点_A \)在\( V_b \)中线的一侧。

无需知道在哪一侧，只要\( V_b \times V_d \)的结果与\( V_b \times V_c \)正负相同，则说明两点在线段的同一侧，反之则在两侧，代表线段相交。

简化运算\( (V_b \times V_d) \times (V_b \times V_c) <= 0 \)即知不在同一侧。

最后还有一个很重要，需要反向再算一次，两者皆成立才能确认线段相交。

如果只算一个，只是延长线可以相交，但实际并不一定有相交。例如

取\( 线段AB \)作中线，判断\( 点_E \)与\( 点_F \)是在\( 线段AB \)两侧，计算结果是相交的，但实际\( 线段AB \)并未经过\( 线段EF \)。这时候只要以\( 线段EF \)作中线再计算一次\( 点_A \)、\( 点_B \)是否在两侧即可。

这只是两条边是否相交，剩下只要逐个判断所有非相邻边是否相交即可。

对于标注场景不会有那么多图形，计算量完全可以接受，大量图形就得上更复杂的算法了。

代码

interface Point {
  x: number;
  y: number;
}
type Edge = [Point, Point];

/**
 * 叉乘
 */
const crossProduct = (v1: number[], v2: number[]) => {
  const [v1x, v1y] = v1;
  const [v2x, v2y] = v2;
  return v1x * v2y - v2x * v1y;
};

/**
 * 是否可以相交
 * @param baseEedge
 * @param targetEdge
 */
const isIntersection = (baseEedge: Edge, targetEdge: Edge) => {
  const [basePointA, basePointB] = baseEedge;
  const [targetPointC, targetPointD] = targetEdge;

  const vBase = [basePointA.x - basePointB.x, basePointA.y - basePointB.y];
  const vBaseC = [basePointA.x - targetPointC.x, basePointA.y - targetPointC.y];
  const vBaseD = [basePointA.x - targetPointD.x, basePointA.y - targetPointD.y];
  return crossProduct(vBase, vBaseC) * crossProduct(vBase, vBaseD) <= 0;
};

/**
 * 提取数组元素
 */
const extractArray = (array: Edge[], startIndex: number, length: number) => {
  const arr = [];
  for (let i = 0; i < length; i++) {
    arr.push(array[(startIndex + i) % array.length]);
  }
  return arr;
};

/**
 * 是否是复杂多边形
 * @param points 多边形的顶点
 */
const isComplexPolygon = (points: Point[]) => {
  const length = points.length;
  if (length < 4) return false;
  const edges = points.reduce<Edge[]>((edges, startPoint, i, array) => {
    const endPoint = array[(i + 1) % length];
    edges.push([startPoint, endPoint]); // [起始点, 结束点]
    return edges;
  }, []);

  // 逐边判断 相邻的边无需判断
  for (const [i, baseEdge] of Object.entries(edges)) {
    const nonadjacentEdge = extractArray(edges, Number(i) + 2, edges.length - 3);
    const flag = nonadjacentEdge.some(
      (edge) => isIntersection(baseEdge, edge) && isIntersection(edge, baseEdge)
    );
    if (flag) return true;
  }
  return false;
};

效果

参考资料

简单多边形判定和修复
平面向量快速入门
向量运算：叉乘
js中常用的数学方法-用于测试形状与形状是否相交