解剖最深奥的Defi协议-- curve V2

接着上一片的curve V1的研究（https://segmentfault.com/a/11...），一直把curve V2的整理拖拉到了现在。真的好难好难～～

背景

在Uniswap v3中，流动性提供者能够定义他们愿意交易的价格来定义区间流动性。这很强大，因为它允许AMM在人们可能想要交易的价格范围内拥有更多可用资金。以前，大宗交易可能会使AMM与市场严重脱节，以至于交易者可能会减少交易量。Uniswap v3方法需要LP非常积极的管理。 curve v2提议将大致相同的系统自动化。 基本上，它根据Curve上的交易确定一个内部价格挂钩，并将流动性集中在这个挂钩上。钉子可以移动，但只有在移动不会导致流动性提供者产生太大的损失时才会这样做。

简介

CurveV2采用的基本理念与UniswapV3非常相似--围绕 "均衡点"聚集流动性。两者都不依靠外部预测器来达到 "均衡点"，而是依靠传统的AMM系统内部的交易博弈，直到系统均衡，curve v2和uniswap v3一样，都非常重视任何外部风险。虽然不依赖于外部因素，但这两种模式，特别是Curve V2，为通向普遍交换道路上的一系列挑战提供了非常优越的解决方案，如极低的无常损失、集中流动性、提高资本效率、低滑点、动态费用等。这当然是由于其 "反常 "的数学模型。

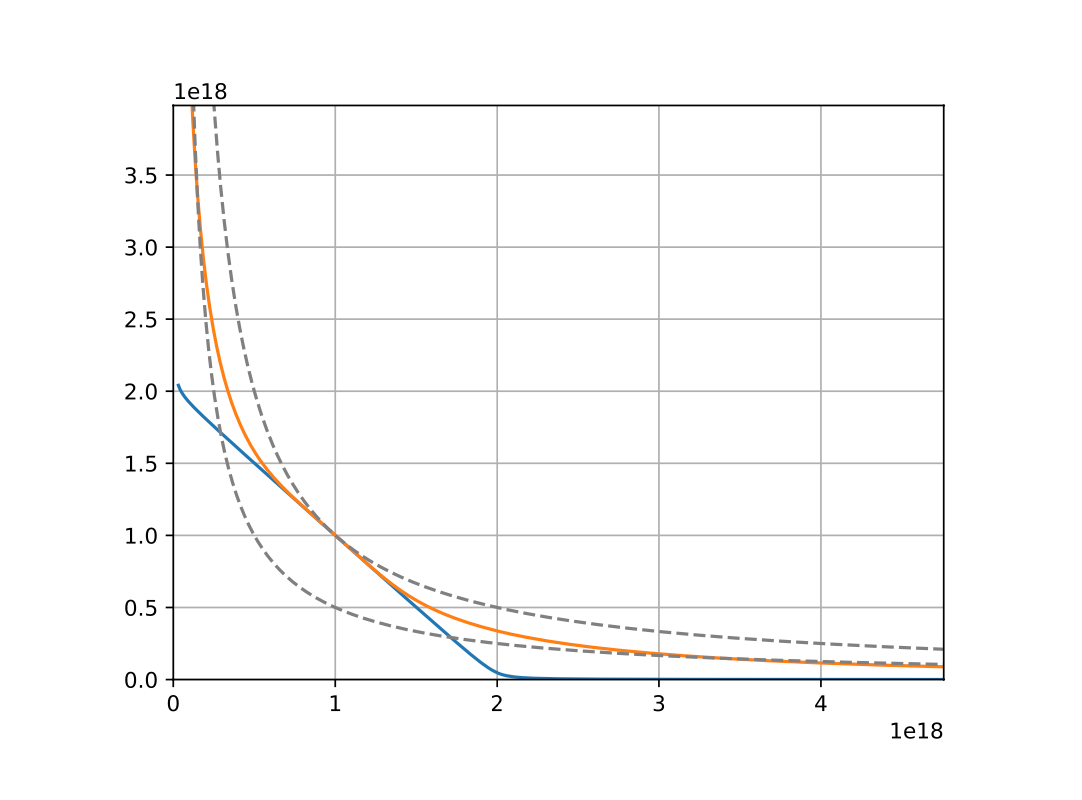
该数学模型最核心的部分是其创造了一种全新的曲线形式。从上图的视觉效果来看，两条虚线是恒定的产品曲线（xy=k和curve v1），蓝线是著名的curve V1稳定的硬币兑换曲线，而曲线V2构造的黄色曲线有两个基本特征--

(1) 它处于xy=1和curve V1曲线之间。

(2) curv1的尾部特征具有明显的xy=1曲线拟合。

所以，curve V2可以解决什么问题？

(a) 它继承了curve V1在 "平衡点 "附近区域的超低滑动性和聚集流动性方面的优势。

(b) 通过在xy=1曲线和curve v1之间，以及在曲线的中间和尾部进行拟合，它获得了xy=1曲线对流动性变化快速反应的优势，避免了池子里的流动性耗尽，对市场的快速变化作出了灵活的反应。

公式推导

在我上一篇Curve V1的数学模型（https://segmentfault.com/a/11...）中，拟合后的曲线的表达式是如下所示。

$$ An^n\sum{x_i} + D = ADn^n + \frac{D^{n+1}}{n^n\prod{x_i}} $$

Curve V2的数学模型和Curve V1类似：

$$K D^{N-1} \sum x_{i}+\prod x_{i}=K D^{N}+\left(\frac{D}{N}\right)^{N}$$

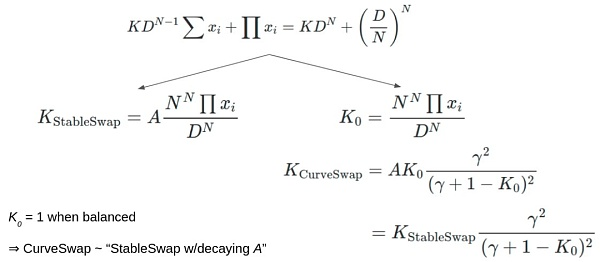
其中，和curve V1一样，Curve V2也有一个杠杠率$K$。这个\(K\)是用来和曲线xy=1拟合的。

$$K_{0}=\frac{\prod x_{i} N^{N}}{D^{N}}, \quad K=A K_{0} \frac{\gamma^{2}}{\left(\gamma+1-K_{0}\right)^{2}}$$

上面这个看起来比较难理解。看下图可能就不难理解了。\( K_{stableswap} \) 是curve v1的常量，我们可以看到curve V2中\( k_{0} \) 是\( K_{stableswap} \)当A=1的时候的特殊情况。所以， \( K_{curveSwap} = K_{StableSwap} \frac{\gamma^{2}}{\left(\gamma+1-K_{0}\right)^{2}} \)。通俗的解释就是，CurveSwap 就是 stableswap 算法中 w / decaying A。

当K0趋于1时，即当曲线形态接近 "平衡点 "范围时（对照图1理解），整个Curve V2的表达方式将退化为Curve V1的表达方式，从而使赎回曲线具有Curve V1的良好特性。

Gamma

公式中引入的最复杂的变量是gamma，它来自图1中的两条恒积曲线。上常量积曲线和curve v1的表达式共同构成了V2常量积曲线的 "平衡点 "区域，而下常量积曲线是上常量积曲线的参数化还原，即

$$ x \cdot y=\left(\frac{D}{N}\right)^{N} $$

我们把常量乘以一个gamma值：

$$ x \cdot y=\gamma \cdot\left(\frac{D}{N}\right)^{N} $$

gamma是一个非常小的正小数，在曲线形状上会比上面的曲线更缩进原点。CurveV2需要引入这样一条gamma曲线，使V2曲线在中段和尾段摆脱curve v1的缺点（流动性枯竭和对汇率变化的快速反应），也就是说，使曲线在后半段有更大的弧度。随着坐标变化不断向横轴和纵轴的远方移动，它们越是向无穷大收敛，V2的曲线形状就越符合下面的常积曲线。也就是说，K0收敛到gamma，CurveV2的表达式就会减少。

$$ A \gamma^{3} D^{N-1} \sum x_{i}+\prod x_{i}=A \gamma^{3} D^{N}+\left(\frac{D}{N}\right)^{N} $$

很明显，这是一条新的曲线，它偏向于下面的恒定产品曲线。在这里，我们只能从混合曲线的基本构造原理出发，反向解释曲线V2表达式的构成，即通过分别向 "平衡 "范围和水平方向和垂直方向的远端靠近，使表达式分别还原为curve V1和恒积曲线。曲线，从而达到curve V2整合Uniswap和curve V1的目的，使这种复杂的混合曲线能够支持普遍的可兑换性，具有更好的集中流动性和滑移性的优势，同时保留Uniswap的流动性保护和应对市场汇率突然变化的优势。

Internal Oracle

CurveV2提出了MarketPrice更新机制，这是一种更新市场的市场价格的机制。更新机制包括：

i)指数移动平均线(EMA)价格

ii)估算利润 （Quantification of a repegging loss）

iii)重新定价算法(取决于i和ii)（Algorithm for repegging）

概括地说，系统通过经典的内部预言机机制EMA不断捕捉系统内的汇率变动序列，然后在每次交易和做市行动后，根据priceoracle不断更新一个名为利润测量\( X_{cp} \)的变量:

$$ X_{c d}=\left(\prod \frac{D}{N p_{i}}\right)^{\frac{1}{N}} $$

报价：

$$ VirtualPrice=X_{CD} / lpsupply $$

监听OldPrice的价格变化，

$$ profit = profit * NewVirtualPrice / OldVirtualPrice $$

这个变量可以解释为每次价格偏离原平衡点的幅度，可以直观地理解为，如果汇率变化不大，系统公式仍以原平衡点为基础，如果汇率变化太大，导致坐标点在曲线上明显偏移，那么系统就应该重建公式，用新的 "平衡点 "基数代替 变量Xcp用来量化改变公式和平衡点的手段。

Adjust

当满足以下条件的时候，调整新的锚定/平衡价格点：

$$ (VirtualPrice - 1) > (profit - 1)/2 + allowedExtraProfit $$

我们可以基于新旧的oracle价格计算出scale值，当scale大于某个阈值的时候，就会更新价格。

$$ \frac{p_{i}}{p_{i, p r e v}}=1+\frac{s}{\sqrt{\sum\left(\frac{p_{j}^{*}}{p_{j, p r e v}}-1\right)^{2}}}\left(\frac{p_{i}^{*}}{p_{i, p r e v}}-1\right) $$

如上所述，当Xcp突破阈值时，系统会根据此时更新的oracleprice更新price_scale，从而定位新公式的新平衡点位置，随后更新新的D值，得到新的表达式。

总结

Curve V2做出了两个创新：新的curve曲线和repegging机制。这个新曲线不仅静态复杂，而且具有动态特性，可以根据EMA和Xcp对系统的偏移做出自动反应，使池子里的流动性在当前汇率范围内得到最大程度的聚集，大大提高了动态资本效率，这是可以超越Uni V3的。

不愧是宇宙第一难defi协议。