图的基础知识
图是一种非常重要的数据结构,用来表示物体与物体之间的关系。图由若干节点及节点之间的边组成。确定图中的节点和边是应用图相关算法解决问题的前提。通常,物体对应图中的节点,如果两个物体存在某种关系,那么它们在图中对应的节点有一条边相连。
图可以分为有向图和无向图。如果给图的每条边规定一个方向,那么这样的图就是有向图,它的边为有向边。有向边就像城市里的单向路,只能沿着一个方向前进。与之相反的是无向图,无向图中的边都没有方向,它的边称为无向边。
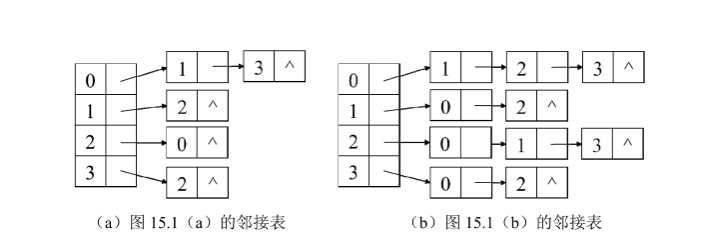
通常,图可以用邻接表或邻接矩阵表示。邻接表为图中的每个节点创建一个容器,第i个容器保存所有与第i个节点相邻的节点。
邻接表
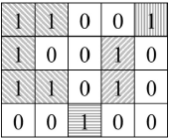
如果一个图中有n个节点,那么它的邻接矩阵M的大小是n×n。如果节点i和节点j之间有一条边,那么Mi等于1;反之,如果节点i和节点j之间没有边,那么Mi等于0。
邻接矩阵
如果一个图是用邻接矩阵表示的,那么判断两个节点之间是否有边相连就非常简单,只需要判断矩阵中对应位置是1还是0即可,时间复杂度为O(1)。但如果一个图中的节点数目非常大但比较稀疏(大部分节点之间没有边),那么邻接表的空间效率更高。
图还可以分为有权图和无权图。在有权图中,每条边都有一个数值权重,用来表示两个节点的某种关系,如两个节点的距离等。在无权图中所有的边都没有权重。
图的搜索
在图中搜索,如找出一条从起始节点到目标节点的路径或遍历所有节点,是与图相关的最重要的算法。按照搜索顺序不同可以将搜索算法分为广度优先搜索和深度优先搜索。
- 广度优先搜索
- 深度优先搜索
技巧
广度优先搜索和深度优先搜索在算法面试中都是非常有用的工具,很多时候使用任意一种搜索算法就能解决某些与图相关的面试题。如果面试题要求在无权图中找出两个节点之间的最短距离,那么广度优先搜索可能是更合适的算法。如果面试题要求找出符合条件的路径,那么深度优先搜索可能是更合适的算法。
前面介绍了如何实现树的广度优先搜索和深度优先搜索。树也可以看成图。实际上,树是一类特殊的图,树中一定不存在环。但图不一样,图中可能包含环。
避免死循环的办法是记录已经搜索过的节点,在访问一个节点之前先判断该节点之前是否已经访问过,如果之前访问过那么这次就略过不再重复访问。
假设一个图有v个节点、e条边。不管是采用广度优先搜索还是深度优先搜索,每个节点都只会访问一次,并且会沿着每条边判断与某个节点相邻的节点是否已经访问过,因此时间复杂度是O(v+e)。
- 最大的岛屿
海洋岛屿地图可以用由0、1组成的二维数组表示,水平或竖直方向相连的一组1表示一个岛屿,请计算最大的岛屿的面积(即岛屿中1的数目)。例如,在图15.5中有4个岛屿,其中最大的岛屿的面积为5。
- 深度优先遍历
/**
* @param {number[][]} grid
* @return {number}
*/
var maxAreaOfIsland = function(grid) {
const rows = grid.length;
const cols = grid[0].length
let visited = new Array(rows).fill().map(() =>new Array(cols).fill(0));
let maxArea = 0;
for(let i = 0; i < rows; i++) {
for(let j = 0; j < cols; j++) {
if(grid[i][j] == 1 && !visited[i][j]) {
const area = getArea(grid, visited, i, j)
maxArea = Math.max(maxArea, area)
}
}
}
return maxArea;
};
var getArea = function(grid, visited, i, j) {
let area = 1;
visited[i][j] = true;
let dirs = [
[-1, 0],
[1, 0],
[0, -1],
[0, 1]
]
for(const dir of dirs) {
const r = i + dir[0];
const c = j + dir[1];
if(r>=0 && r < grid.length && c>=0 && c < grid[0].length && grid[r][c] === 1 && !visited[r][c]) {
area += getArea(grid, visited, r, c)
}
}
return area;
};- 广度优先遍历
var getArea = function(grid, visited, i, j) {
const queue = new Array();
queue.push([i,j])
visited[i][j] = true
let dirs = [
[-1, 0],
[1, 0],
[0, -1],
[0, 1]
]
let area = 0;
while(queue.length) {
let pos = queue.shift();
area++;
for(const dir of dirs) {
const r = pos[0] + dir[0];
const c = pos[1] + dir[1];
if(r>=0 && r < grid.length && c>=0 && c < grid[0].length && grid[r][c] === 1 && !visited[r][c]) {
queue.push([r,c])
visited[r][c] = true
}
}
}
return area
}- 二分图
如果能将一个图中的节点分成A、B两个部分,使任意一条边的一个节点属于A而另一个节点属于B,那么该图就是一个二分图。输入一个由数组graph表示的图,graph[i]中包含所有和节点i相邻的节点,请判断该图是否为二分图。
/**
* @param {number[][]} graph
* @return {boolean}
*/
var isBipartite = function(graph) {
const size = graph.length;
const colors = new Array(size).fill(-1)
for(let i = 0; i<size; ++i) {
if(colors[i] == -1) {
if(!setColor(graph, colors, i, 0)) {
return false
}
}
}
return true
};
var setColor = function(graph, colors, i, color) {
const queue = []
queue.push(i)
color[i] = color
while(queue.length) {
let v = queue.pop()
for(const neighbor of graph[v]) {
if(colors[neighbor] >=0) {
if(colors[neighbor] == colors[v]) {
return false;
}
} else {
queue.push(neighbor)
colors[neighbor] = 1 - colors[v];
}
}
}
return true
}
var setColor = function(graph, colors, i, color) {
const queue = [];
queue.push(i)
colors[i] = color;
while(queue.length) {
let v = queue.shift()
for(let neighbor of graph[v]) {
if(colors[neighbor] >= 0) {
if (colors[neightbor] == colors[v]) {
return false
}
} else {
queue.push(neighbor);
colors[neighbor] = 1 - colors[v];
}
}
}
return true
}- 深度优先遍历
- 矩阵的距离
输入一个由0、1组成的矩阵M,请输出一个大小相同的矩阵D,矩阵D中的每个格子是矩阵M中对应格子离最近的0的距离。水平或竖直方向相邻的两个格子的距离为1。假设矩阵M中至少有一个0。
广度优先搜索
效率特别差,这种方法/** * @param {number[][]} mat * @return {number[][]} */ var updateMatrix = function(mat) { const row = mat.length; const col = mat[0].length; const grid = new Array(row).fill().map(() => new Array(col).fill(Infinity)) const queue = [] for(let i = 0; i < row; i++) { for(let j = 0; j < col; j++) { if(mat[i][j] == 0) { queue.push([i, j]) grid[i][j] = 0 } } } const dirs = [[-1, 0], [1, 0], [0, 1], [0, -1]]; while(queue.length) { const pos = queue.pop(); const dist = grid[pos[0]][pos[1]] for(const dir of dirs) { const r = pos[0] + dir[0] const c = pos[1] + dir[1] if(r>=0 && r<row && c >= 0 && c < col) { if(grid[r][c] > dist+1) { grid[r][c] = dist + 1 queue.push([r,c]) } } } } return grid };
如果输入矩阵的大小为m×n,那么以矩阵为背景的图中的节点数为O(mn),边的数目也是O(mn),因此上述解法的时间复杂度是O(mn)。
- 单词的演变
输入两个长度相同但内容不同的单词(beginWord和endWord)和一个单词列表,求从beginWord到endWord的演变序列的最短长度,要求每步只能改变单词中的一个字母,并且演变过程中每步得到的单词都必须在给定的单词列表中。如果不能从beginWord演变到endWord,则返回0。假设所有单词只包含英文小写字母。
/**
* @param {string} beginWord
* @param {string} endWord
* @param {string[]} wordList
* @return {number}
*/
var ladderLength = function (beginWord, endWord, wordList) {
let notVisited = new Map();
for(let word of wordList) {
notVisited.set(word);
}
if(!notVisited.has(endWord)) return 0;
let map1 = new Map();
let map2 = new Map();
let res = 2;// 两个方向 距离初始化为 2
map1.set(beginWord);
map2.set(endWord);
notVisited.delete(endWord);
while(map1.size !== 0 && map2.size !== 0) {
if(map1.size > map2.size){//每次都从节点数目少的方向搜索
[map1,map2] = [map2,map1];
}
let map3 = new Map();
for(let word of map1.keys()){
let neighbors = getNeighbors(word);
for(let neighbor of neighbors) {
if(map2.has(neighbor)) {
return res;
}
if(notVisited.has(neighbor)) {
map3.set(neighbor);
notVisited.delete(neighbor);
}
}
}
res++;
map1 = map3;
}
return 0;
};
const getNeighbors = (word) => {
let neighbors = new Array();
for (let i = 0; i < word.length; i++) {
let temp = Array.from(word);
let old = temp[i].charCodeAt(0);
for (let j = 97; j <= 122; j++) {
if (old !== j) {
temp[i] = String.fromCharCode(j);
neighbors.push(temp.join(''));
}
}
temp = Array.from(word);
}
return neighbors;
};- 开密码锁
一个密码锁由4个环形转轮组成,每个转轮由0~9这10个数字组成。每次可以上下拨动一个转轮,如可以将一个转轮从0拨到1,也可以从0拨到9。密码锁有若干死锁状态,一旦4个转轮被拨到某个死锁状态,这个锁就不可能打开。密码锁的状态可以用一个长度为4的字符串表示,字符串中的每个字符对应某个转轮上的数字。输入密码锁的密码和它的所有死锁状态,请问至少需要拨动转轮多少次才能从起始状态"0000"开始打开这个密码锁?如果锁不可能打开,则返回-1。
var openLock = function(deadends, target) {
if (target === '0000') {
return 0;
}
const dead = new Set(deadends);
if (dead.has("0000")) {
return -1;
}
let step = 0;
const queue = [];
queue.push("0000");
const seen = new Set();
seen.add("0000");
while (queue.length) {
++step;
const size = queue.length;
for (let i = 0; i < size; ++i) {
const status = queue.shift();
for (const nextStatus of get(status)) {
if (!seen.has(nextStatus) && !dead.has(nextStatus)) {
if (nextStatus === target) {
return step;
}
queue.push(nextStatus);
seen.add(nextStatus);
}
}
}
}
return -1;
};
const numPrev = (x) => {
return x === '0' ? '9' : (parseInt(x) - 1) + '';
}
const numSucc = (x) => {
return x === '9' ? '0' : (parseInt(x) + 1) + '';
}
// 枚举 status 通过一次旋转得到的数字
const get = (status) => {
const ret = [];
const array = Array.from(status);
for (let i = 0; i < 4; ++i) {
const num = array[i];
array[i] = numPrev(num);
ret.push(array.join(''));
array[i] = numSucc(num);
ret.push(array.join(''));
array[i] = num;
}
return ret;
}- 所有路径
一个有向无环图由n个节点(标号从0到n-1,n≥2)组成,请找出从节点0到节点n-1的所有路径。图用一个数组graph表示,数组的graph[i]包含所有从节点i能直接到达的节点。例如,输入数组graph为[[1,2],[3],[3],[]],则输出两条从节点0到节点3的路径,分别为0→1→3和0→2→3
var allPathsSourceTarget = function(graph) {
const stack = [], ans = [];
const dfs = (graph, x, n) => {
if (x === n) {
ans.push(stack.slice());
return;
}
for (const y of graph[x]) {
stack.push(y);
dfs(graph, y, n);
stack.pop();
}
}
stack.push(0);
dfs(graph, 0, graph.length - 1);
return ans;
};
/**
* @param {number[][]} graph
* @return {number[][]}
*/
var allPathsSourceTarget = function(graph) {
const result = [];
const path = []
dfs(0, graph, path, result)
return result
};
var dfs = function (source, graph, path, result) {
path.push(source)
const length = path.length
if(source == (graph.length - 1)) {
result.push(path.slice())
} else {
for(const next of graph[source]) {
dfs(next, graph, path, result)
}
}
path.splice(length - 1)
}- 计算除法
输入两个数组equations和values,其中,数组equations的每个元素包含两个表示变量名的字符串,数组values的每个元素是一个浮点数值。如果equations[i]的两个变量名分别是Ai和Bi,那么Ai/Bi=values[i]。再给定一个数组queries,它的每个元素也包含两个变量名。对于queries[j]的两个变量名Cj和Dj,请计算Cj/Dj的结果。假设任意values[i]大于0。如果不能计算,那么返回-1。
我们可以将整个问题建模成一张图:给定图中的一些点(变量),以及某些边的权值(两个变量的比值),试对任意两点(两个变量)求出其路径长(两个变量的比值)。
因此,我们首先需要遍历 \textit{equations}equations 数组,找出其中所有不同的字符串,并通过哈希表将每个不同的字符串映射成整数。
在构建完图之后,对于任何一个查询,就可以从起点出发,通过广度优先搜索的方式,不断更新起点与当前点之间的路径长度,直到搜索到终点为止。
/**
* @param {string[][]} equations
* @param {number[]} values
* @param {string[][]} queries
* @return {number[]}
*/
var calcEquation = function(equations, values, queries) {
let nvars = 0;
const variables = new Map();
const n = equations.length;
for (let i = 0; i < n; i++) {
if (!variables.has(equations[i][0])) {
variables.set(equations[i][0], nvars++);
}
if (!variables.has(equations[i][1])) {
variables.set(equations[i][1], nvars++);
}
}
// 对于每个点,存储其直接连接到的所有点及对应的权值
const edges = new Array(nvars).fill(0);
for (let i = 0; i < nvars; i++) {
edges[i] = [];
}
for (let i = 0; i < n; i++) {
const va = variables.get(equations[i][0]), vb = variables.get(equations[i][1]);
edges[va].push([vb, values[i]]);
edges[vb].push([va, 1.0 / values[i]]);
}
const queriesCount = queries.length;
const ret = [];
for (let i = 0; i < queriesCount; i++) {
const query = queries[i];
let result = -1.0;
if (variables.has(query[0]) && variables.has(query[1])) {
const ia = variables.get(query[0]), ib = variables.get(query[1]);
if (ia === ib) {
result = 1.0;
} else {
const points = [];
points.push(ia);
const ratios = new Array(nvars).fill(-1.0);
ratios[ia] = 1.0;
while (points.length && ratios[ib] < 0) {
const x = points.pop();
for (const [y, val] of edges[x]) {
if (ratios[y] < 0) {
ratios[y] = ratios[x] * val;
points.push(y);
}
}
}
result = ratios[ib];
}
}
ret[i] = result;
}
return ret;
};- 最长递增路径
输入一个整数矩阵,请求最长递增路径的长度。矩阵中的路径沿着上、下、左、右4个方向前行。例如,图15.14中矩阵的最长递增路径的长度为4,其中一条最长的递增路径为3→4→5→8,如阴影部分所示。
/**
* @param {number[][]} matrix
* @return {number}
*/
var longestIncreasingPath = function(matrix) {
if(matrix.length == 0 || matrix[0].length == 0) {
return 0;
}
let lengths = new Array(matrix.length).fill(0).map(() => new Array(matrix[0].length).fill(0));
let longest = 0;
for(let i = 0;i < matrix.length;i++) {
for(let j = 0;j < matrix[0].length;j++) {
let length = dfs(matrix,lengths,i,j);
longest = Math.max(longest,length);
}
}
return longest;
};
const dfs = (matrix,lengths,i,j) => {
if(lengths[i][j] !== 0) return lengths[i][j];// 说明已经计算过
let rows = matrix.length;
let cols = matrix[0].length;
let dirs = [[-1,0],[1,0],[0,1],[0,-1]];
let length = 1;
for(let dir of dirs){
let r = i + dir[0];
let c = j + dir[1];
if(r >= 0 && r < rows && c >= 0 && c < cols && matrix[i][j] < matrix[r][c]){
let path = dfs(matrix,lengths,r,c);
length = Math.max(path + 1,length);
}
}
lengths[i][j] = length;
return length;
}拓扑排序(TODO)
- 什么是拓扑排序
给定一个包含 n 个节点的有向图 G,我们给出它的节点编号的一种排列,如果满足:
对于图 G 中的任意一条有向边 (u, v),u 在排列中都出现在 v 的前面。
那么称该排列是图 G 的「拓扑排序」。根据上述的定义,我们可以得出两个结论:
那么称该排列是图 G 的「拓扑排序」。根据上述的定义,我们可以得出两个结论:
- 如果图 G 中存在环(即图 G 不是「有向无环图」),那么图 G 不存在拓扑排序。
- 如果图 G 是有向无环图,那么它的拓扑排序可能不止一种。
- 课程顺序
n门课程的编号为0~n-1。输入一个数组prerequisites,它的每个元素prerequisites[i]表示两门课程的先修顺序。如果prerequisites[i]=[ai,bi],那么必须先修完bi才能修ai。请根据总课程数n和表示先修顺序的prerequisites得出一个可行的修课序列。如果有多个可行的修课序列,则输出任意一个可行的序列;如果没有可行的修课序列,则输出空序列。
本题是一道经典的「拓扑排序」问题。
- 广度优先搜索
这种应该是最好理解的。
/**
* @param {number} numCourses
* @param {number[][]} prerequisites
* @return {number[]}
*/
var findOrder = function(numCourses, prerequisites) {
const graph = new Map();
// 构建图
for(let i = 0; i < numCourses; i++) {
graph.set(i, [])
}
// 构建入度数组
let inDegrees = new Array(numCourses).fill(0);
// 将图的关系构建起来
for(const prere of prerequisites) {
graph.get(prere[1]).push(prere[0])
inDegrees[prere[0]]++ // 入度记录
}
// 构建队列用于遍历
const queue = [];
// 找到入度为0,添加到队列
for(let i = 0; i < numCourses; i++) {
if(inDegrees[i] == 0) {
queue.push(i)
}
}
// 记录顺序,作为返回结果
const order = [];
while(queue.length) {
let course = queue.shift();
order.push(course);
for(let next of graph.get(course)) {
inDegrees[next]--
if(inDegrees[next] === 0) {
queue.push(next);
}
}
}
return order.length == numCourses ? order : []
};时间复杂度: O(n+m), 空间复杂度: O(n+m)
- 深度优先搜索
我发现leetCode题解并没有人用js写深入,就很真实
- 外星文字典
现有一种使用英语字母的外星文语言,这门语言的字母顺序与英语顺序不同。给定一个字符串列表 words ,作为这门语言的词典,words 中的字符串已经 按这门新语言的字母顺序进行了排序 。请你根据该词典还原出此语言中已知的字母顺序,并 按字母递增顺序 排列。若不存在合法字母顺序,返回 "" 。若存在多种可能的合法字母顺序,返回其中 任意一种 顺序即可。
这很明显也是拓扑排序,难的地方在于,给出的word的先后关系不能保证是2个节点,中间可能穿插n个节点
/**
* @param {string[]} words
* @return {string}
*/
var alienOrder = function(words) {
let valid = true;
const edges = new Map();
const indegrees = new Map();
const length = words.length;
for (const word of words) {
const wordLength = word.length;
for (let j = 0; j < wordLength; j++) {
const c = word[j];
if (!edges.has(c)) {
edges.set(c, []);
}
}
}
const addEdge = (before, after) => {
const length1 = before.length, length2 = after.length;
const length = Math.min(length1, length2);
let index = 0;
while (index < length) {
const c1 = before[index], c2 = after[index];
if (c1 !== c2) {
edges.get(c1).push(c2);
indegrees.set(c2, (indegrees.get(c2) || 0) + 1);
break;
}
index++;
}
if (index === length && length1 > length2) {
valid = false;
}
}
for (let i = 1; i < length && valid; i++) {
addEdge(words[i - 1], words[i]);
}
if (!valid) {
return "";
}
const queue = [];
const letterSet = edges.keys();
for (const u of letterSet) {
if (!indegrees.has(u)) {
queue.push(u);
}
}
const order = [];
while (queue.length) {
const u = queue.shift();
order.push(u);
const adjacent = edges.get(u);
for (const v of adjacent) {
indegrees.set(v, indegrees.get(v) - 1);
if (indegrees.get(v) === 0) {
queue.push(v);
}
}
}
return order.length === edges.size ? order.join('') : "";
};

**粗体** _斜体_ [链接](http://example.com) `代码` - 列表 > 引用。你还可以使用@来通知其他用户。