卷积神经网络 (CNN) 得到了广泛的应用并且事实证明他是非常成功的。但是卷积的计算很低效,滑动窗口需要很多计算并且限制了过滤器的大小,通常在 [3,3] 到 [7,7] 之间的小核限制了感受野(最近才出现的大核卷积可以参考我们以前的文章),并且需要许多层来捕获输入张量的全局上下文(例如 2D 图像)。图像越大小核的的表现就越差。这就是为什么很难找到处理输入高分辨率图像的 CNN模型。
有一种方法可以将核大小扩展到 [1024,1024] 及以上,并且这种方法可以增加给定输入分辨率的核大小并且对推理时间几乎没有影响,还可以大幅降低特征图的空间维度,并且不会丢失几乎任何信息,你相信吗?
所有这些特征都基于一个简单的数学性质:傅里叶变换的卷积定理(准确地说是互相关定理)
卷积的问题
让我们回顾一些基础知识。卷积是应用于两个函数的数学运算。让我们从一维案例开始:
连续一维卷积
离散一维卷积
换句话说:取两个信号,保留一个然后围绕坐标轴翻转另一个信号。将固定信号上的翻转信号从负无穷移动到正无穷(或直到信号的所有非零部分都已重叠)。对于每一步计算元素乘积并对所有值求和。结果值就是此步骤的卷积结果。
但是为什么我之前提到了互相关呢?那是因为卷积和互相关实际上是相以同的方式计算的,唯一的区别是过滤器(核)被翻转了。这由不同的符号表示:
TensorFlow 和 PyTorch 实际上是在计算输入信号和可学习卷积核的互相关,而不是卷积本身。由于卷积核是由网络学习的,因此卷积核是否翻转并不重要。网络会自己弄清楚什么是最好的结果。框架甚至可以节省一些计算而不进行翻转操作。但是有一个区别,如果卷积核是固定的,当你加载一个训练好的模型时,应该知道它是使用互相关还是卷积训练的,因为需要知道最终是否翻转的权重。
上面说的主要总结为两个问题:
- 计算输出序列中的单个点需要进行大量计算。
- 输入信号越大(即图像的分辨率越高),核必须更频繁地移动,因此需要更多的计算。同样适用于大核。
更多的计算意味着更多的内存和更大的计算延迟。CNN在较低的输入分辨率和更小的过滤器。更少的像素意味着更少的细节,更小的过滤器会导致更小的感受野。网络需要有多个连续的卷积层,以增加感受野。网络变得更深,这再次在训练期间带来了新的挑战。
二维离散傅里叶变换
从数学上讲,时间变量 t 的实数或复数函数 x(t) 的傅里叶变换是实数频率变量 f 的复数函数 X(f):
也可以说我们将信号从时域投影到频域。通过这样做可以受益于傅里叶变换的特殊性质,即卷积定理和相关定理。
卷积定理
互相关定理
这些概念非常重要也是本文的基础:时域中的卷积/相关对应于频域中的简单元素乘法。但这有什么用的呢?如前所述,卷积需要很多计算,尤其是对于大像素图像和大核。它的复杂性与序列长度成二次方,即 O(N²)。根据卷积定理,我们只需要对变换后的输入和变换后的核进行逐元素的乘法。并且计算傅里叶变换的高效算法,即快速傅里叶变换 (FFT)可将复杂度降低到 O(N log(N))。而且更重要的是只要核比输入信号小,那么计算的复杂度就是恒定的。所以核大小是 [3,3] 还是 [1024, 1024] 并不重要。
傅里叶变换也适用于实数或复数离散信号 x[k],它分配实变量 n 的复数离散信号 X[n]:
一维卷积
二维卷积
离散傅里叶变换 (DFT) 是用于数字信号处理,而计算机以离散值存储信号。所以在使用 DFT 时,我们需要记住:
- 假设输入信号是周期性的,并且对整个周期进行采样
- 产生的频谱是周期性的
图像可以解释为空间信号而不是时间信号。在计算机上图像是空间离散的,因为值存储在像素中这些像素从具有空间分布单元的图像传感器采样而被数字化。
二维 DFT(以及 2D 连续傅里叶变换)可以分成连续的 1D DFT,其中行和列可以分别计算。
这有两个优点:首先,可以重用 1D DFT 的算法;其次,它有助于为 2D DFT 建立直觉,因为可以单独解释行和列。
但离散傅里叶变换有一个小细节:卷积定理不适用于 DFT。两个信号的 DFT 相乘对应于它们的循环卷积,由运算符 ⊛ 表示,而不是它们的线性卷积。
上图为DFT的循环卷积定理公式
循环卷积是一个以信号长度 N 的重复周期性信号,而线性卷积的长度为 (N+F-1),其中 F 是滤波器信号(核)的长度。因此如果盲目地在频域中取乘积,会将长度为 (N+M-1) 的信号压缩到长度 N。它可以被视为时域中的混叠,从而在最终结果中产生不希望的伪影。但是循环和线性卷积会共享的值,即 (N-F+1)。而剩余的 (F-1) 值被包裹并干扰信号的其他值。
如果包裹干扰的值为零,这不就意味着没有干扰了吗?我们可以从循环卷积重建线性卷积。当用至少 (F-1) 个零填充信号时,包裹的值就不会干扰实际值。我们可以循环地将包裹的值移回其位置并裁剪填充的值。
现在我们已经介绍了理论,让我们看看一些 2D 傅里叶变换并加强我们对 2D 傅里叶变换的理解。
基本测试信号及其对 CNN 的影响
考虑一个像素强度遵循对角正弦波的图像。可以通过沿图像的每个轴将 2D 傅里叶变换分离为多个 1D 傅里叶变换来计算 2D 傅里叶变换。如果沿着水平轴行走,就会遇到重复的图案。如果沿着垂直轴行走,情况也是如此。因此在第四象限(右下),即频率分量为正的象限,很自然地会期望频谱有一个高值。
注:二维幅度谱通常在绘制时使用对数函数进行缩放,无论图像内容如何图像都具有高偏移量,因为它们通常以无符号整数表示,仅表示正值。
现在,让我们考虑一个具有不同边长的矩形的输入图像。如果再次沿着每个轴行走,会遇到一个在水平轴上具有短脉冲宽度的矩形和一个在垂直轴上具有较宽脉冲宽度的矩形。如果熟悉信号理论,会立即想到的频谱具有某种 sinc 函数,其中 sinc(x)=sin(x)/x。
如果你想到的是一个 sinc 函数,那么你是完全正确的。频谱由沿两个轴的 sinc 函数组成。在这里可以做一个基本的观察:水平轴有更高的频率分量作为垂直轴,零交叉在水平轴上更分散。这里有两个含义:
- 输入图像中的窄空间特征在幅度谱中具有高频分量,因此它们具有高带宽。高带宽滤波器容易产生噪声。
- 光谱与输入图像中特征的空间长度成反比。窄特征导致宽谱,宽特征导致窄谱。
这对我们的带有小核的 CNN 意味着什么,比如 3x3 像素?根据我们上面的观察,这应该意味着具有小核的 CNN 充当高带宽滤波器,因此容易产生输入噪声。核尺寸越大,滤波器的带宽越低,选择性越强。
图像的二维 DFT 和频域滤波
我们已经讨论了一些基本信号,现在让我们研究真实图像的 2D DFT。
频谱的中心代表零频率,也称为偏移。离中心越远,输入中的频率分量就越高。考虑到这一点,可以轻松导出高通滤波器和低通滤波器。
高通滤波器抑制低频并保留高频分量。这种行为可以通过一个滤波器来实现,该滤波器在近中心的值设为0,而将远离中心的值设为1。滤波器的作用是将滤波器与频谱相乘,然后计算傅里叶反变换。
如上图所示,高通滤波器可以用作边缘检测器。图像中的边缘以像素值的突然变化为特征,因此具有高梯度。梯度越高,涉及的频率越高。
另一方面,低通滤波器抑制高频分量并保留低频分量。低通滤波器可以通过在中心区域为 1 而在外部区域为 0 的掩码来实现。
低通滤波后的图像会变得模糊清晰度降低,计算机视觉中使用的一种典型滤波器是高斯滤波器。它也是一个低通滤波器,但是它并不是突然截止频率,而是会随着频率的升高而逐渐增,所以会使图像平滑。
上图的图像模糊,但失真较小。并且看起来更平滑。
用于机器学习应用的一个非常有趣的核是矩形核。卷积神经网络通常会逐渐减小空间宽度并增加通道数。池化,例如最大池化或平均池化通常用于减小空间宽度。如果我们在频域中进行池化是如何操作的呢?
通过在频域中应用矩形滤波器,我们可以大幅去除频率分量,而不会对空间域中的图像质量产生很大影响。
DFT 对于实际输入有一个有趣的特性:它关于原点是共轭对称的。对称性意味着频谱包含在计算过程中可以省略这样可以进一步加快计算。下图显示了这种变换及其从频谱重建的图像。
TensorFlow 中的实现
上面介绍了使用离散傅里叶变换实现线性卷积的理论知识。下面我们进行实际操作
我们需要完成以下 6 个步骤:
- 填充输入图像以避免时域中的混叠
- 将滤波器填充到图像大小准备逐元素乘法
- 计算输入图像和滤波器的 2D rFFT
- 转换后的输入和转换后的过滤器的元素乘法
- 计算滤波输入的 2D 逆 rFFT 以获得循环卷积
- 从循环卷积重构线性卷积
1、填充输入图像
为了避免时域中的混叠效应,我们需要用至少 (F-1) 个零填充图像,其中 F 是滤波器的边长。此外计算 DFT 的 FFT 算法对于 2 次方的信号长度(例如 128,512,1024)特别有效。
填充输入图像至少有两个选项:1、手动填充图像。2、将 FFT 的序列长度设置为填充信号的长度。
下面的代码手动填充图像。
def GetImagePadding(filterSize):
'''
returns the one sided padding to pad an image.
'''
return int((filterSize-1)/2)
def FillImageShapeToPower2(imageShape):
'''
fills the image shape to the next higher power of 2 value.
imageShape: Expected to be of shape [batch, channels, height, width]
'''
width = imageShape[-1]
log2 = np.log2(width)
newPower = int(np.ceil(log2))
newShape = 2**newPower
newShape = (imageShape[0],imageShape[1],newShape,newShape)
return newShape
def PadImage(image, filterShape):
'''
returns a padded image considering the size of the filter and the next higher power of 2 value
'''
input_shape = tf.shape(image)
paddingFilter = GetImagePadding(filterShape[0])
finalShape = FillImageShapeToPower2(input_shape+(0,0,2*paddingFilter,2*paddingFilter))
final_padding = int((finalShape[-1]-input_shape[-1])/2)
paddings = [[0,0],
[final_padding,final_padding],
[final_padding,final_padding],
[0,0],
]
image_padded = tf.pad(image,paddings)
return image_padded下面是我在计算 FFT 时指定更高序列长度的首选方法:
# image is of shape [b,c,h,w]
padding = GetImagePadding(filter_shape[0])
image_shape = (input_shape[0],
input_shape[1],
input_shape[2]+2*padding,
input_shape[3]+2*padding)image_shape = FillImageShapeToPower2(image_shape)
F_image = tf.signal.rfft2d(image, fft_length=[image_shape[-2],image_shape[-1]])2、将滤波器填充到图像大小
由于需要计算变换后的图像与变换后的滤波器的元素乘积,因此我们需要在计算傅里叶变换之前将滤波器用零填充填充图像。通过正确设置 FFT 计算的 fft_lenght 参数来填充滤波器,即
F_filter = tf.signal.rfft2d(filter, fft_length=[image_shape[-2],image_shape[-1]])3、计算 2D rFFT
准备好输入信号后,可以计算填充图像和填充滤波器的 FFT:
# Image shape [b,c,h,w], Filter shape [out, in , k, k]
F_image = tf.signal.rfft2d(image, fft_length=[image_shape[-2],image_shape[-1]])
F_filter = tf.signal.rfft2d(filter, fft_length=[image_shape[-2],image_shape[-1]])利用实际输入的共轭对称性,仅使用 rfft2d 计算 2D 信号的实际 FFT。输入未填充的信号并将 fft_length 设置为大于输入长度的值。这会自动用零填充信号。
提示:TensorFlow 的 rfft2d 实现在输入的最后两个维度上计算 FFT。与 numpy 的实现不同,并且不能通过参数更改维度。因此图像的形状是 [batch, channel, height, width],滤波器的形状是 [output_filter, input_filter, kernel_height,kernel_width]
如果我们是在频域中实现卷积,这样的工作就完成了。由于TensorFlow实际上是使用的互相关,所以需要对变换后的滤波器进行共轭以获得一致的结果:
F_filter = tf.math.conj(F_filter)4、元素乘法
如果我们只有一个图像和一个核,那么逐元素乘法将只是 F_image*F_filter。但在实际场景中,通常以批处理的形式处理多个图像,并且并行应用多个核。所以需要重新排列输入信号的维度,并利用数组广播来执行此操作,这样不涉及循环操作。
@tf.function
def ElementwiseProduct(a, b):
'''
calculates the elementwise product multiple times taking advantage of array broadcasting.
Is slower as the matrix multiplication, but requires less memory!
'''
a = tf.einsum("bihw->bhwi",a)
a = tf.expand_dims(a,-1) #[b,h,w,in,1]
b = tf.einsum("oihw->hwio",b) #[h, w, in, out]
c = a*b #[b,h,w,in,out] due to broadcasting
c = tf.einsum("bhwio->bohwi",c)
c = tf.math.reduce_sum(c, axis=-1) #[b, out, h, w]
return cTensorFlow 的 einsum() 函数可用于重塑维度。箭头左侧的字符描述输入形状,右侧的字符描述输出形状。图像和过滤器的尺寸进行重新对齐,当计算元素乘积时,所有批次和所有输出过滤器都将被广播。在乘法之后,通过重新重塑维度和减小输入滤波器的维度来恢复初始形状。
5、计算2D 逆 rFFT
逆 FFT 具有与 FFT 相同的 fft_length 参数:
out = tf.signal.irfft2d(filterd_image, fft_length=[image_shape[-2],image_shape[-1]])6、循环卷积重建线性卷积
#Circular shift
out = tf.roll(out,shift = [2*padding,2*padding],axis = [-2,-1])
#Truncation
out = tf.slice(out,
begin = [0, 0, padding, padding],
size=[input_shape[0],
filter_shape[-1],
input_shape[2],
input_shape[3]]
)所有步骤就完成了,下面的代码汇总了整个实现:
def CalcDFT2D(image, filter):
'''
Calculates the cross-correlation in the Frequency domain
image: [batch, channel, height, width]
filter: [height, width, inp_filter, out_filter]
'''
# 0. Preprocess Inputs
input_shape = tf.shape(image) #[batchsize, im_channel, im_height, im_width]
filter_shape = tf.shape(filter) #[kernel_H, kernel_W, inp_filter, out_filter]
filter = tf.einsum("hwio->oihw",filter) # [kernel,kernel,inp_filter,out_filter]->[out_filter, inp_filter, kernel, kernel]
# 1. & 2. Pad image and Filter:
# Required to avoid aliasing in spatial domain: circular convolution
# calculates padding which is used to update image shape. Padding happens during FFT by setting fft_length
padding = GetImagePadding(filter_shape[0])
image_shape = (input_shape[0],input_shape[1],input_shape[2]+2*padding,input_shape[3]+2*padding)
image_shape = FillImageShapeToPower2(image_shape)
# 3. Fourier Transform image and filter
F_image = tf.signal.rfft2d(image, fft_length=[image_shape[-2],image_shape[-1]])
F_filter = tf.signal.rfft2d(filter, fft_length=[image_shape[-2],image_shape[-1]])
F_filter = tf.math.conj(F_filter) #to be equvivalent to the cross correlation
# 4. Apply filter by elementwise Multiplication
filterd_image = ElementwiseProduct(F_image,F_filter)
# 5. inverse DFT on filtered image
out = tf.signal.irfft2d(filterd_image, fft_length=[image_shape[-2],image_shape[-1]])
# 6. Reconstruct linear convolution from circular convolution
out = tf.roll(out,shift = [2*padding,2*padding],axis = [-2,-1])
out = tf.slice(out, begin = [0, 0, padding, padding], size=[input_shape[0], filter_shape[-1], input_shape[2], input_shape[3]])
return out验证
我们这写操作这真的有用吗?让我们来验证一下
首先,我们将查看两个函数(tf.nn.conv2d()和我们的实现)在不同的核大小中的执行时间(以秒为单位)。
2D卷积的执行时间随着核大小的增加而不断增长。而2D DFT卷积在执行时间上是恒定的,与滤波器的大小无关。这是因为滤波器被填充到图像的大小。如果滤波器更大,则填充的值可以更少。
现在让我们来看看结果的差异。我们在720x720像素的图像上应用一个3x3大小的核函数,并使用8个核。通过两种算法运行它,并计算绝对差的平均值和标准差。
convResult = CalcConv(image, filter)
dftResult = CalcDFT2D(image, filter)
error = tf.math.abs(convResult-dftResult)
mean = tf.math.reduce_mean(error)
std = tf.math.reduce_std(error)
# Mean Absolute Error: 0.001560982083901763
# Standard deviation: 0.0015975720016285777均值和标准差都很低。这种差异来自于数字的不准确性。当观察滤波后的图像及其对应的振幅谱时,我们可以看到它们是基本是一致的。
直接比较滤波后的图像和二维光谱。
2D线性卷积结果
2D DFT卷积结果
结论
本文介绍了卷积和DFT背后的数学理论,通过观察不同的光谱获得了一些想发,并且通过TensorFlow进行了实现,并验证了结果的正确性。
本文的设计在频域而不是空间域工作的,可能还不完善但是却给出了一些新的想法,特别是对于大输入图像和大尺寸核的处理上。在使用频域似乎有违现有的理论,但实际上可以加快计算速度。
本文的完整代码请参考下面地址
https://avoid.overfit.cn/post/503f3087e31c4b8fa6b53fee007559a0
作者:Sascha Kirch
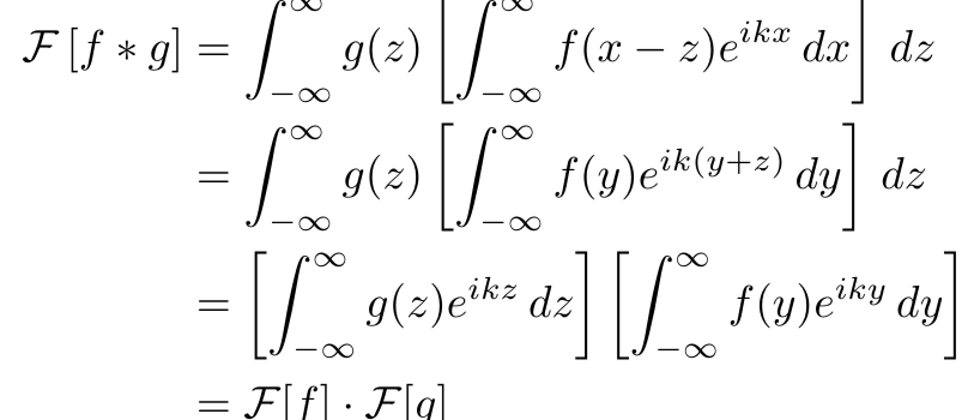

























**粗体** _斜体_ [链接](http://example.com) `代码` - 列表 > 引用。你还可以使用@来通知其他用户。