时间序列的蒙特卡罗交叉验证

交叉验证应用于时间序列需要注意是要防止泄漏和获得可靠的性能估计本文将介绍蒙特卡洛交叉验证。这是一种流行的TimeSeriesSplits方法的替代方法。

时间序列交叉验证

TimeSeriesSplit通常是时间序列数据进行交叉验证的首选方法。下图1说明了该方法的操作方式。可用的时间序列被分成几个大小相等的折叠。然后每一次折首先被用来测试一个模型，然后重新训练它。除了第一折只用于训练。

使用TimeSeriesSplit进行交叉验证的主要好处如下:

• 它保持了观察的顺序。这个问题在有序数据集(如时间序列)中非常重要。
• 它生成了很多拆分 。几次拆分后可以获得更稳健的评估。如果数据集不大，这一点尤其重要。

TimeSeriesSplit的主要缺点是跨折叠的训练样本量是不一致的。这是什么意思?

假设将该方法应用于图1所示的5次分折。在第一次迭代中，所有可用观测值的20%用于训练。但是，这个数字在上次迭代中是80%。因此，初始迭代可能不能代表完整的时间序列。这个问题会影响性能估计。

那么如何解决这个问题?

蒙特卡罗交叉验证

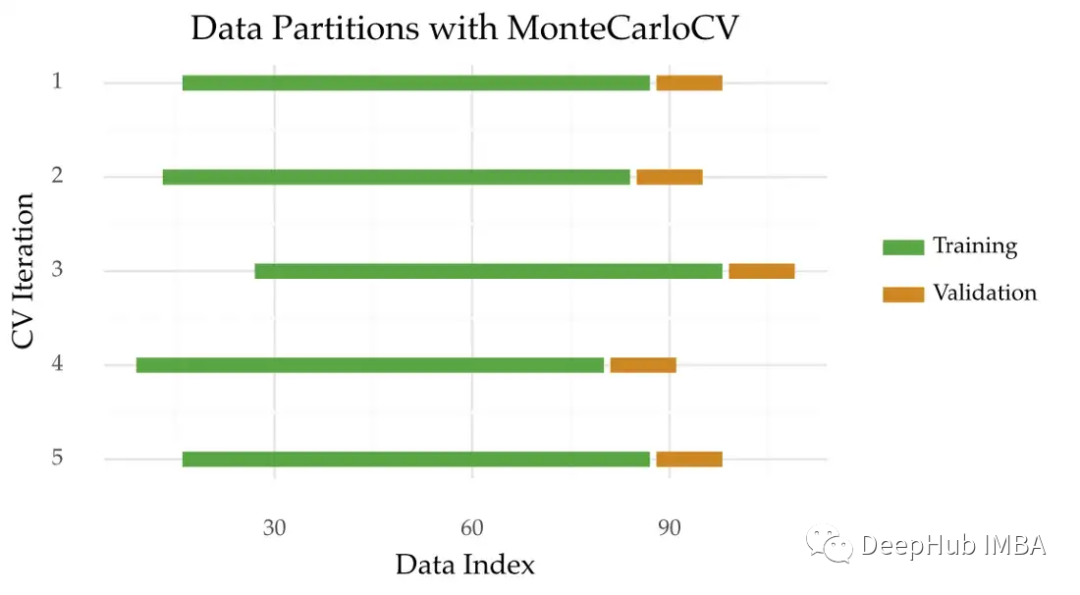
蒙特卡罗交叉验证(MonteCarloCV)是一种可以用于时间序列的方法。这个想法是在不同的随机起点来获取一个时间周期的数据，下面是这种方法的可视化描述:

像TimeSeriesSplit一样，MonteCarloCV也保留了观测的时间顺序。它还会保留多次重复估计过程。

MonteCarloCV与TimeSeriesSplit的区别主要有两个方面:

• 对于训练和验证样本量，使用TimeSeriesSplit时训练集的大小会增加。在MonteCarloCV中，训练集的大小在每次迭代过程中都是固定的，这样可以防止训练规模不能代表整个数据;
• 随机的分折，在MonteCarloCV中，验证原点是随机选择的。这个原点标志着训练集的结束和验证的开始。在TimeSeriesSplit的情况下，这个点是确定的。它是根据迭代次数预先定义的。

MonteCarloCV最初由Picard和Cook使用。详细信息可以查看参考文献[1]。

经过详细研究MonteCarloCV。这包括与TimeSeriesSplit等其他方法的比较。MonteCarloCV可以获得更好的估计，所以我一直在使用它。你可以在参考文献[2]中查看完整的研究。

不幸的是，scikit-learn不提供MonteCarloCV的实现。所以，我们决定自己手动实现它:

 from typing import List, Generator
 
 import numpy as np
 
 from sklearn.model_selection._split import _BaseKFold
 from sklearn.utils.validation import indexable, _num_samples
 
 
 class MonteCarloCV(_BaseKFold):
 
     def __init__(self,
                  n_splits: int,
                  train_size: float,
                  test_size: float,
                  gap: int = 0):
         """
         Monte Carlo Cross-Validation
 
         Holdout applied in multiple testing periods
         Testing origin (time-step where testing begins) is randomly chosen according to a monte carlo simulation
 
         :param n_splits: (int) Number of monte carlo repetitions in the procedure
         :param train_size: (float) Train size, in terms of ratio of the total length of the series
         :param test_size: (float) Test size, in terms of ratio of the total length of the series
         :param gap: (int) Number of samples to exclude from the end of each train set before the test set.
         """
 
         self.n_splits = n_splits
         self.n_samples = -1
         self.gap = gap
         self.train_size = train_size
         self.test_size = test_size
         self.train_n_samples = 0
         self.test_n_samples = 0
 
         self.mc_origins = []
 
     def split(self, X, y=None, groups=None) -> Generator:
         """Generate indices to split data into training and test set.
         Parameters
         ----------
         X : array-like of shape (n_samples, n_features)
             Training data, where `n_samples` is the number of samples
             and `n_features` is the number of features.
         y : array-like of shape (n_samples,)
             Always ignored, exists for compatibility.
         groups : array-like of shape (n_samples,)
             Always ignored, exists for compatibility.
         Yields
         ------
         train : ndarray
             The training set indices for that split.
         test : ndarray
             The testing set indices for that split.
         """
 
         X, y, groups = indexable(X, y, groups)
         self.n_samples = _num_samples(X)
 
         self.train_n_samples = int(self.n_samples * self.train_size) - 1
         self.test_n_samples = int(self.n_samples * self.test_size) - 1
 
         # Make sure we have enough samples for the given split parameters
         if self.n_splits > self.n_samples:
             raise ValueError(
                 f'Cannot have number of folds={self.n_splits} greater'
                 f' than the number of samples={self.n_samples}.'
             )
         if self.train_n_samples - self.gap <= 0:
             raise ValueError(
                 f'The gap={self.gap} is too big for number of training samples'
                 f'={self.train_n_samples} with testing samples={self.test_n_samples} and gap={self.gap}.'
             )
 
         indices = np.arange(self.n_samples)
 
         selection_range = np.arange(self.train_n_samples + 1, self.n_samples - self.test_n_samples - 1)
 
         self.mc_origins = \
             np.random.choice(a=selection_range,
                              size=self.n_splits,
                              replace=True)
 
         for origin in self.mc_origins:
             if self.gap > 0:
                 train_end = origin - self.gap + 1
             else:
                 train_end = origin - self.gap
             train_start = origin - self.train_n_samples - 1
 
             test_end = origin + self.test_n_samples
 
             yield (
                 indices[train_start:train_end],
                 indices[origin:test_end],
             )
 
     def get_origins(self) -> List[int]:
         return self.mc_origins

MonteCarloCV接受四个参数:

n_splitting:分折或迭代的次数。这个值趋向于10;

training_size:每次迭代时训练集的大小与时间序列大小的比值;

test_size:类似于training_size，但用于验证集;

gap:分离训练集和验证集的观察数。与TimeSeriesSplits一样，此参数的值默认为0(无间隙)。

每次迭代的训练和验证大小取决于输入数据。我发现一个0.6/0.1的分区工作得很好。也就是说，在每次迭代中，60%的数据被用于训练。10%的观察结果用于验证。

实际使用的例子

下面是配置的一个例子:

 from sklearn.datasets import make_regression
 from src.mccv import MonteCarloCV
 
 X, y = make_regression(n_samples=120)
 
 mccv = MonteCarloCV(n_splits=5, 
                     train_size=0.6, 
                     test_size=0.1, 
                     gap=0)
 
 for train_index, test_index in mccv.split(X):
     print("TRAIN:", train_index, "TEST:", test_index)
     X_train, X_test = X[train_index], X[test_index]
     y_train, y_test = y[train_index], y[test_index]

该实现也与scikit-learn兼容。以下是如何结合GridSearchCV:

 from sklearn.ensemble import RandomForestRegressor
 from sklearn.model_selection import GridSearchCV
 
 model = RandomForestRegressor()
 param_search = {'n_estimators': [10, 100]}
 
 gsearch = GridSearchCV(estimator=model, cv=mccv, param_grid=param_search)
 gsearch.fit(X, y)

我希望你发现MonteCarloCV有用!

引用

[1] Picard, Richard R., and R. Dennis Cook. “Cross-validation of regression models.” Journal of the American Statistical Association 79.387 (1984): 575–583.

[2] Vitor Cerqueira, Luis Torgo, and Igor Mozetič. “Evaluating time series forecasting models: An empirical study on performance estimation methods.” Machine Learning 109.11 (2020): 1997–2028.

https://avoid.overfit.cn/post/d6ab5b4cd0e5476c91cae97c4564deb9

作者：Vitor Cerqueira